算法数据结构

算法学习

发布日期: 2022-08-13

更新日期: 2023-11-16

文章字数: 8.4k

阅读时长: 41 分

一、排序算法

1.1 快速排序

确定分界点x：$q[1]$、$q[(1+r)/2]$、$q[r]$、随机
调整区间：保证所有小于等于 $x$ 的数在 $x$ 的左区间，大于等于 $x$ 的数在 $x$ 的右区间
递归处理左右两段

调整区间可实现的方法：

方法1

开额外的数组 $a[]$、$b[]$
扫描 $q[1:r]$
- 当 $q[i]\leq x$ 时，将 $x$ 插入到 $a[]$
- 当 $q[i]\geq x$ 时，将 $x$ 插入到 $b[]$
分别将 $a[]$、$b[]$ 中的数放在 $q$ 中

方法2

$i,j$ 指针分别指向第一个和末尾一个，并分别向右向左移动

选择基准值：从待排序的数据中选择一个基准值（pivot）。通常情况下，可以选择第一个元素、最后一个元素、中间元素等作为基准值。

分区操作：将数组或列表中的元素重新排列，使得比基准值小的元素位于基准值的左边，比基准值大的元素位于右边。同时，基准值所在的位置也已经确定了，通常称之为分区操作或划分操作。

递归排序：对基准值左右两侧的子序列分别进行快速排序，直到整个序列有序。

合并结果：当递归过程结束后，整个数组就变成了有序的。

快速排序的关键在于分区操作，可以采用以下步骤进行分区：

设置两个指针left和right，它们分别指向数组的最左端和最右端。

从右向左移动right指针，直到找到一个小于基准值的元素。

从左向右移动left指针，直到找到一个大于基准值的元素。

交换left和right指针所指向的元素。

重复上述步骤，直到left和right指针相遇。

将基准值与left指针所指向的元素交换。

void quick_sort(int q[], int l, int r)
{
    if (l >= r) return;					   // 判边界
    int x = q[l], i = l - 1, j = r + 1;		// 当数据经过加强时,应取区间中点x = q[(l + r) / 2]或随机点
    while (i < j)
    {
        do i ++ ; while (q[i] < x);
        do j -- ; while (q[j] > x);
        if (i < j) swap(q[i], q[j]);
    }
    quick_sort(q, l, j), quick_sort(q, j + 1, r);
}

1.2 归并排序

是一种稳定排序，采用分治的思想。

确定分界点：mid = (l + r) / 2
递归排序left、right
归并，合二为一

void merge_sort(int q[], int l, int r)
{
    if (l >= r) return;

    int mid = l + r >> 1;
    merge_sort(q, l, mid);
    merge_sort(q, mid + 1, r);

    int k = 0, i = l, j = mid + 1;	 	// 指针的初始位置为两个已经排序序列的起始位置
    while (i <= mid && j <= r)
        if (q[i] <= q[j]) tmp[k++] = q[i++];
        else tmp[k++] = q[j++];

    while (i <= mid) tmp[k++] = q[i++];
    while (j <= r) tmp[k++] = q[j++];

    for (i = l, j = 0; i <= r; i ++, j ++ ) q[i] = tmp[j];
}

例：逆序对的数量

给定一个长度为 $n$ 的整数数列，请你计算数列中的逆序对的数量。

逆序对的定义如下：对于数列的第 $i$ 个和第 $j$ 个元素，如果满足 $i<j$ 且 $a[i]>a[j]$，则其为一个逆序对；否则不是。

我们发现一个性质：当数组分为左右两部分时，其中一个部分中的数字位置进行了交换并不会影响另外一部分与该部分之间产生的逆序对数（也就是“一左一右”的情况）。根据归并排序流程，发现可以用归并排序排序。

则，如果右侧指针指向的数字小于左侧指针指向的数字，那么说明左侧指针所指向的数字以及该序列之后的数字均大于右侧指针所指向的数字，所及将这些数字全部记录，ans += mid - i + 1即可。

#include<iostream>
using namespace std;
const int N = 100010;
int a[N];
long long count = 0;

void merge_sort(int q[], int l, int r)
{
    if (l >= r) return;
    int tmp[N];
    int mid = l + r >> 1;
    merge_sort(q, l, mid);
    merge_sort(q, mid + 1, r);

    int k = 0, i = l, j = mid + 1;
    while (i <= mid && j <= r)
        if (q[i] <= q[j]) tmp[k++] = q[i++];
        else {
            tmp[k++] = q[j++];
            count += mid - i + 1;
        }

    while (i <= mid) tmp[k++] = q[i++];
    while (j <= r) tmp[k++] = q[j++];

    for (i = l, j = 0; i <= r; i++, j++) q[i] = tmp[j];
}

int main()
{
    int n;
    cin >> n;
    for (int i = 0; i < n; i++)
    {
        cin >> a[i];
    }
    merge_sort(a, 0, n - 1);

    cout << count << endl;
}

二、二分算法

2.1 整数二分算法

整数二分算法的应用场景：

找大于等于数的第一个位置（满足某个条件的第一个数）
找小于等于数的最后一个数（满足某个条件的最后一个数）
查找最大值（满足该边界的右边界）
查找最小值（满足该边界的左边界）

整数二分算法检查一个数的范围是否满足某种性质，通过二分算法将一列数分为红色区间（满足性质）和绿色区间（不满足性质），找到边界。

二分并不是找某个数，而是找到符合条件的最小的数或最大的数。

Case 1：二分红色区间分界点 mid = (l + r + 1) / 2，if(check(mid))：//检查mid是否满足某种性质

若为true，则mid取在红色区间内，答案（区间）更新为[mid, r]，l = mid；
若为false，则mid取在绿色区间内，答案（区间）更新为[l, mid - 1]，r = mid - 1。

Case 2：二分绿色区间分界点 mid = (l + r) / 2，if(check(mid))：

若为true，则mid取在红色区间内，答案（区间）更新为[1, mid]，r = mid；
若为false，则mid取在绿色区间内，答案（区间）更新为[mid + 1, r]，l = mid + 1。

技巧：

根据图形二分哪个边界，性质是什么，每次二分后选择答案所在的区间进行处理

mid是否要加一，看check函数满足后是r = mid(不加一)还是l = mid(加一)即可。

bool check(int x) {/* ... */} 			// 检查x是否满足某种性质

// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用：
int bsearch_1(int l, int r)
{
    while (l < r)
    {
        int mid = l + r + 1 >> 1;
        if (check(mid)) l = mid;		// check()判断mid是否满足性质
        else r = mid - 1;
    }
    return l;
}

// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用：
int bsearch_2(int l, int r)
{
    while (l < r)
    {
        int mid = l + r >> 1;
        if (check(mid)) r = mid;
        else l = mid + 1;
    }
    return l;
}

例1：数的范围

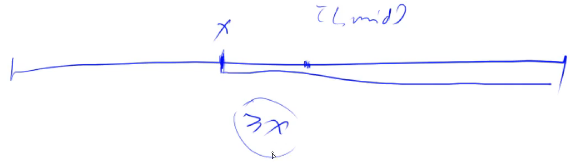
给定一个按照升序排列的长度为 $n$ 的整数数组，以及 $q$ 个查询。

对于每个查询，返回一个元素 $k$ 的起始位置和终止位置（位置从 $0$ 开始计数）。

如果数组中不存在该元素，则返回 -1 -1。

数的范围演示

#include<iostream>
using namespace std;
const int N = 100100;
int n, m;
int q[N];

int main()
{
    scanf("%d%d", &n, &m);
    for(int i = 0; i < n; i++) scanf("%d", &q[i]);
    while(m--)
    {
        int x;
        scanf("%d", &x);
        int l = 0, r = n - 1;
        while(l < r)
        {
            int mid = l + r >> 1;
            if(q[mid] >= x) r = mid;
            else l = mid + 1;
        }
        if (q[l] != x) printf("-1 -1\n");		// 循环退出后有 l == r,原问题无解
        else
        {
            printf("%d ", l);
            // 左边都满足 <= x,右边不满足
            int l = 0, r = n - 1;
            while(l < r)
            {
                int mid = l + r + 1 >> 1;
                if(q[mid] <= x) l = mid;
                else r = mid - 1;
            }
            printf("%d\n",l);
        }
    }
}

例2：四平方和

四平方和定理，又称为拉格朗日定理：

每个正整数都可以表示为至多 $4$ 个正整数的平方和。

如果把 $0$ 包括进去，就正好可以表示为 $4$ 个数的平方和。

比如：

$5=0^2 +0^2+1^2+2^2$
$7=1^2+1^2+1^2+2^2$

对于一个给定的正整数，可能存在多种平方和的表示法。

要求你对 $4$ 个数排序：

$0≤a≤b≤c≤d$

并对所有的可能表示法按 $a,b,c,d$ 为联合主键升序排列，最后输出第一个表示法。

信息：

最多只能枚举两个数
用空间换时间

for(int c = 0; c * c <= N; c ++)
    for(int d = c; c * c + d * d <= N; d ++)
        // 	将 c * c + d * d 存起来

枚举 a、b，查询 $c^2+d^2$ 的值的结果是否存在：

for(int a = 0; a * a <= N; a ++)
    for(int b = a; a * a + b * b <= N; b ++)
    {
        t = n - a * a - b * b;
        // if(t在前面出现过) ...	哈希/二分
    }

如果找到字典序最小的解 —> 存到结构体中并排序，找到 $t=n-a^2-b^2$ 字典序最小的组合

运用二分算法的时间复杂度为 $O(N^2logN)$

#include <cstring>
#include <iostream>
#include <algorithm>
#include <cmath>

using namespace std;

const int N = 2500010;

struct Sum
{
    int s, c, d;
    bool operator< (const Sum &t)const
    {
        if (s != t.s) return s < t.s;
        if (c != t.c) return c < t.c;
        return d < t.d;
    }
}sum[N];

int n, m;

int main()
{
    cin >> n;

    for (int c = 0; c * c <= n; c ++ )
        for (int d = c; c * c + d * d <= n; d ++ )
            sum[m ++ ] = {c * c + d * d, c, d};

    sort(sum, sum + m);

    for (int a = 0; a * a <= n; a ++ )
        for (int b = 0; a * a + b * b <= n; b ++ )
        {
            int t = n - a * a - b * b;
            int l = 0, r = m - 1;
            while (l < r)
            {
                int mid = l + r >> 1;
                // 找到大于等于差值最小的一个数
                if (sum[mid].s >= t) r = mid;
                else l = mid + 1;
            }
            
            if (sum[l].s == t)
            {
                printf("%d %d %d %d\n", a, b, sum[l].c, sum[l].d);
                return 0;
            }
        }

    return 0;
}

2.2 浮点数二分算法

bool check(double x) {/* ... */} 	// 检查x是否满足某种性质

double bsearch_3(double l, double r)
{
    const double eps = 1e-6;   		// eps 表示精度，取决于题目对精度的要求
    while (r - l > eps)
    {
        double mid = (l + r) / 2;
        if (check(mid)) r = mid;
        else l = mid;
    }
    return l;
}

例：数的三次方根

#include<iostream>
using namespace std;
int main()
{
    double x;
    cin >> x;
    double l = -10000, r = 10000;
    while(r - l > 1e-8)
    {
        double mid = (l + r) /2;
        if(mid * mid * mid >= x)
        {
            r = mid;
        }
        else
        {
            l = mid;
        }
    }
    printf("%lf\n",l);
    return 0;
}

三、高精度

大整数通过数组存储，数组每一位存一位数字，小端形式。

3.1 高精度加法

// C = A + B, A >= 0, B >= 0
vector<int> add(vector<int> &A, vector<int> &B)		// 使用引用传递, 提高效率
{
    if (A.size() < B.size()) return add(B, A);

    vector<int> C;
    int t = 0;
    for (int i = 0; i < A.size(); i ++ )
    {
        t += A[i];
        if (i < B.size()) t += B[i];
        C.push_back(t % 10);
        t /= 10;
    }

    if (t) C.push_back(t);
    return C;
}

例：高精度加法

#include <iostream>
#include <vector>
using namespace std;
vector<int> add(vector<int> &A, vector<int> &B)
{
    if (A.size() < B.size()) return add(B, A);	// 为了方便计算，让A中保存较长的数字， B中保存较短的数字

    vector<int> C;		// 保存结果的数组
    int t = 0;			// 进位，开始时是0
    for (int i = 0; i < A.size(); i ++ )		// 依次计算每一位
    {
        t += A[i];		// 加上 A 的第 i 位上的数字
        if (i < B.size()) t += B[i];			// 加上 B 的第 i 位上的数字
        C.push_back(t % 10); 				    // C 中放入结果
        t /= 10;							   // t 更新成进位
    }

    if (t) C.push_back(t);					   // 最后如果进位上有数，放进结果数组
    return C;								  // 返回结果
}

int main()
{
    string a, b;
    vector<int> A, B;
    cin >> a >> b;
    for (int i = a.size() - 1; i >= 0; i -- ) A.push_back(a[i] - '0');	//倒序存储第一个数
    for (int i = b.size() - 1; i >= 0; i -- ) B.push_back(b[i] - '0');	//倒序存储第二个数
    auto C = add(A, B);			//调用加和函数
    for (int i = C.size() - 1; i >= 0; i -- ) cout << C[i];			   //倒序输出C中的数字
    cout << endl;
    return 0;
}

3.2 高精度减法

$A_{3}A_{2}A_{1}A_{0}-B_{2}B_{1}B_{0}$

对每位进行计算：$A_{i}-B_{i}-t$，有：

$\geq 0$，$A_{i}-B_{i}-t$
$<0$，借一位并补上10，$A_{i}-B_{i}+10-t$

计算A-B，有：

当$A\geq B$时，A-B
当$A<B$时，-(B-A)

// C = A - B, 满足A >= B, A >= 0, B >= 0
vector<int> sub(vector<int> &A, vector<int> &B)
{
    vector<int> C;
    for (int i = 0, t = 0; i < A.size(); i ++ )
    {
        t = A[i] - t;
        if (i < B.size())	t -= B[i];
        C.push_back((t + 10) % 10);
        if (t < 0)	t = 1;
        else t = 0;
    }
    
    while (C.size() > 1 && C.back() == 0) C.pop_back();
    return C;
}

例：高精度减法

#include<iostream>
#include<vector>
using namespace std;

// 判断是否有 A >= B
bool cmp(vector<int>& A, vector<int>& B)
{
	if (A.size() != B.size())
		return A.size() > B.size();
	for (int i = A.size() - 1; i >= 0; i--)
	{
		if (A[i] != B[i])
			return A[i] > B[i];
	}
	return true;
}

// C = A - B
vector<int> sub(vector<int>& A, vector<int>& B)
{
	vector<int> C;
	for (int i = 0, t = 0; i < A.size(); i++)
	{
		t = A[i] - t;
		if (i < B.size()) t -= B[i];
		C.push_back((t + 10) % 10);
		if (t < 0) t = 1;
		else t = 0;
	}
	while (C.size() > 1 && C.back() == 0)
		C.pop_back();	// 去除前导0
	return C;
}

int main()
{
	string a, b;
	vector<int> A, B;
	cin >> a >> b;		// a = "123456"
	for (int i = a.size() - 1; i >= 0; i--)
	{
		A.push_back(a[i] - '0'); 	// A = [6,5,4,3,2,1]
	}
	for (int i = b.size() - 1; i >= 0; i--)
	{
		B.push_back(b[i] - '0');
	}
	if (cmp(A, B))
	{
		auto C = sub(A, B);
		for (int i = C.size() - 1; i >= 0; i--)
		{
			cout << C[i];
		}
	}
	else {
		auto C = sub(B, A);
		cout << "-";
		for (int i = C.size() - 1; i >= 0; i--)
		{
			cout << C[i];
		}
	}
	return 0;
}

3.3 高精度乘法

3.3.1 高精度乘低精度

手算模拟：每个被乘数位与B的整体进行相乘

A 1 2 3

B 1 2

$C_{3}C_{2}C_{1}C_{0}$

每位分别是：

$C_{0}=(3*12)%10=6$

$t_{1}=(3*12)/10=3$

$C_{1}=(2*12+t_{1})%10=7$

$t_{2}=2$

$C_{2}=(1*12+t_{2})%10=4$

$t_{3}=1$

$C_{3}=1$

// C = A * b, A >= 0, b >= 0
vector<int> mul(vector<int> &A, int b)
{
    vector<int> C;

    int t = 0;
    for (int i = 0; i < A.size() || t; i ++ )
    {
        if (i < A.size()) t += A[i] * b;
        C.push_back(t % 10);
        t /= 10;
    }

    while (C.size() > 1 && C.back() == 0) C.pop_back();

    return C;
}

例：高精度与低精度的乘法

#include<iostream>
#include<vector>
using namespace std;
vector<int> mul(vector<int>& A, int b)
{
	vector<int> C;
	int t = 0;
	for (int i = 0; i < A.size() || t; i++)
	{
		if (i < A.size()) t += A[i] * b;
		C.push_back(t % 10);
		t /= 10;
	}
	while (C.size() > 1 && C.back() == 0)
		C.pop_back();	// 去除前导0
	return C;
}
int main()
{
	string a;
	int b;
	cin >> a >> b;
	vector<int> A;
	for (int i = a.size() - 1; i >= 0; i--)
		A.push_back(a[i] - '0');
	auto C = mul(A, b);
	for (int i = C.size() - 1; i >= 0; i--)
		cout << C[i];
	return 0;
}

3.3.2 高精度乘高精度

例：大数运算

vector<int> mul(vector<int>& A, vector<int>& B)
{
    vector<int> C(A.size() + B.size());
    for (int i = 0; i < A.size(); i ++ )
        for (int j = 0; j < B.size(); j ++ )
            C[i + j] += A[i] * B[j];

    for (int i = 0, t = 0; i < C.size(); i ++ )
    {
        t += C[i];
        C[i] = t % 10;
        t /= 10;
    }

    while (C.size() > 1 && C.back() == 0) C.pop_back();
    return C;
}

3.4 高精度除以低精度

流程：

从最高位开始处理，上一次的余数 ×10 再加上当前位上的数字（被除数，我们令它为 A）；
往答案数组中压入 ⌊A/B⌋（这里 B 表示除数），然后将余数更新为 A mod B；
重复以上操作。

// A / b = C ... r, A >= 0, b > 0
vector<int> div(vector<int> &A, int b, int &r)
{
    vector<int> C;
    r = 0;
    for (int i = A.size() - 1; i >= 0; i -- )
    {
        r = r * 10 + A[i];
        C.push_back(r / b);
        r %= b;
    }
    reverse(C.begin(), C.end());
    while (C.size() > 1 && C.back() == 0) C.pop_back();
    return C;
}

例：高精度除法

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
// A / b,商是c,余数是r
vector<int> div(vector<int>& A, int b, int& r)
{
	vector<int> C;	// 商
	r = 0;
	// 除法从最高位开始,为了统一加减乘,需要逆序
	for (int i = A.size() - 1; i >= 0; i--)
	{
		r = r * 10 + A[i];
		C.push_back(r / b);
		r %= b;
	}
	reverse(C.begin(), C.end());	// algorithm头文件中的函数
	while (C.size() > 1 && C.back() == 0)
		C.pop_back();	// 去除前导0
	return C;
}
int main()
{
	string a;
	int b;
	cin >> a >> b;
	vector<int> A;
	for (int i = a.size() - 1; i >= 0; i--)
	{
		A.push_back(a[i] - '0');
	}
	int r;
	auto C = div(A, b, r);
	for (int i = C.size() - 1; i >= 0; i--)
	{
		cout << C[i];
	}
	cout << endl << r << endl;
	return 0;
}

四、前缀和

4.1 一维前缀和

前缀和表示为：$S_{i}=a_{1}+a_{2}+…+a_{i}$（S[0]=0），下标从1开始

**求$S_{i}$**：for(i = 1; i <= n; i++) {S[i] = S[i-1] + a[i];}
作用：范围为[l,r]数组的和，若没有前缀和数组，时间复杂度为O(n)；运用前缀和数组，可以用S[r]-S[l-1]进行计算，时间复杂度为O(1)

#include<iostream>
using namespace std;

const int N = 100010;
int n, m;
int a[N], s[N];

int main()
{
	scanf("%d%d", &n, &m);
	for (int i = 1; i <= n; i++)
	{
	    scanf("%d", &a[i]); 
	}
	for (int i = 1; i <= n; i++)
	{
		s[i] = s[i - 1] + a[i];				// 前缀和的初始化
	}
	while (m--)
	{
		int l, r;
		scanf("%d%d", &l, &r);
		printf("%d\n", s[r] - s[l - 1]);	 // 区间和的计算
	}
	return 0;
}

例1：最大子序和

输入一个长度为 $n$ 的整数序列，从中找出一段长度不超过 $m$ 的连续子序列，使得子序列中所有数的和最大。

最优化问题分析法：集合思想。应用：在一个有限集合中求最值，或者求个数。

问题可转化为求结尾为 $a[k]$ 的子序列中长度不超过 $m$ 且子序列和最大，即 $Max;S[k]-S[k-j](1\leq j\leq m,0\leq k \leq n)$。求特定区间和可以用前缀和来快速求得，求出滑动窗口的最值可以用单调队列来求解。

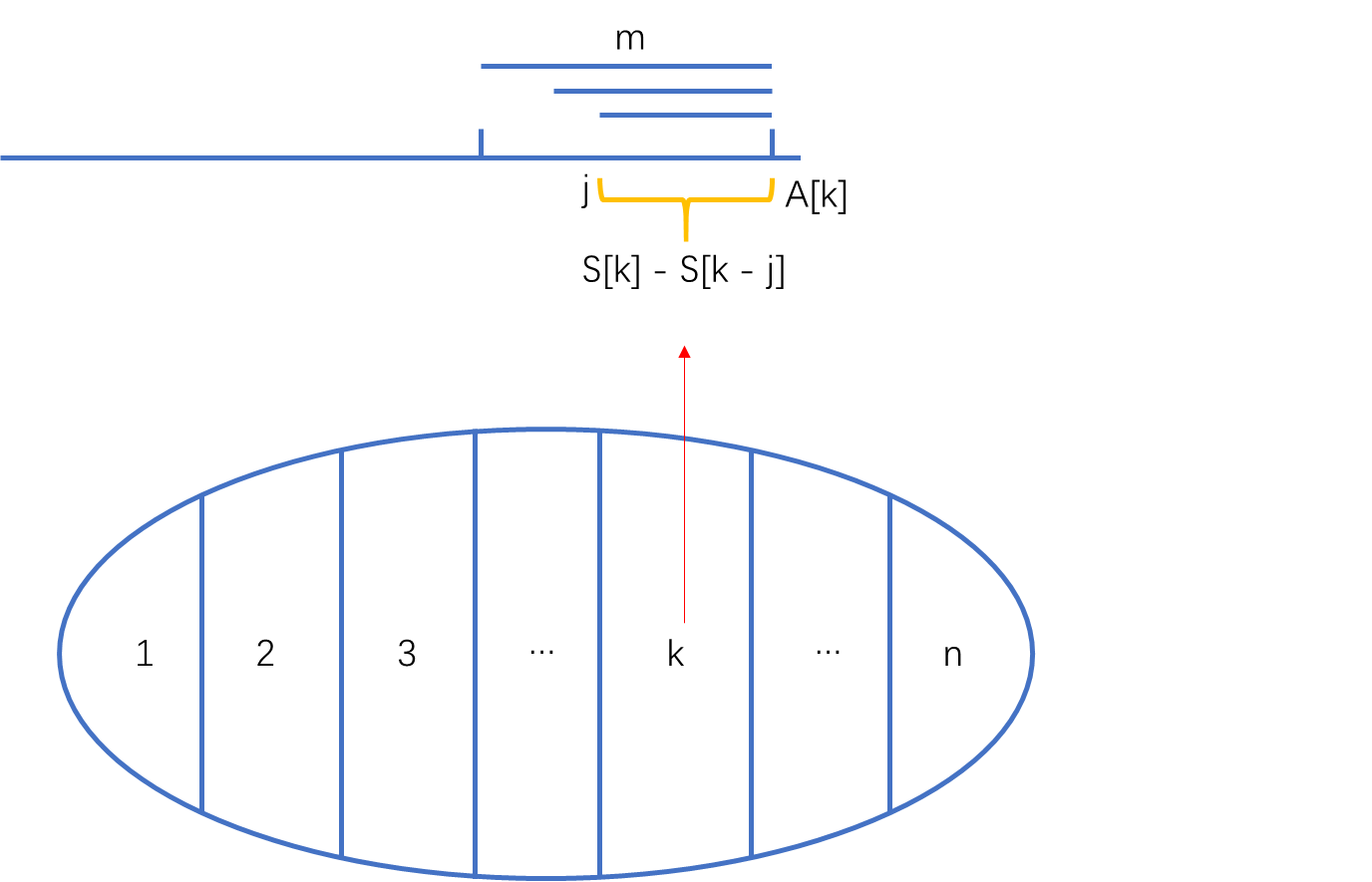
注：**$tt$ 初始值为 $0$ 的原因**：从头开始的情况

由于求解的是在 $i$ 之前，不包括 $i$ 的长度为 $m$ 的滑动窗口的最小值，当前 $m$ 个元素为正值时，$s[i]$ 递增，这时窗口内最小值为 $s[0]$，表示取 $1\sim i$ 个元素求和，所以应在队列里插入一个 $0$，也就是 $s[0]$。

#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 300010, INF = 1e9;

int n, m;
int s[N];
int q[N];

int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i ++ ) scanf("%d", &s[i]), s[i] += s[i - 1];

    int res = -INF;
    int hh = 0, tt = 0;

    for (int i = 1; i <= n; i ++ )
    {
        if (q[hh] < i - m) hh ++ ;
        res = max(res, s[i] - s[q[hh]]);
        while (hh <= tt && s[q[tt]] >= s[i]) tt -- ;
        q[ ++ tt] = i;
    }

    printf("%d\n", res);

    return 0;
}

例2：(CSP考试)期末预测之最佳阈值

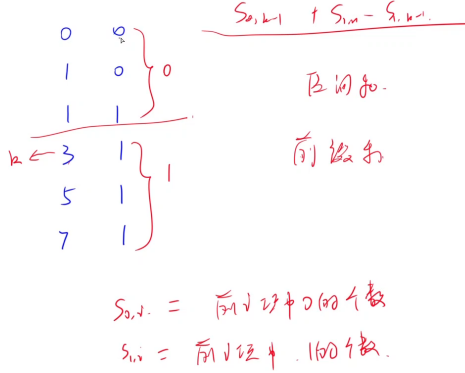
$S_{0,i}=前i项中0的个数$
$S_{1,i}=前i项中1的个数$
$预测结果=S_{0,k-1}+S_{1,n}-S_{1,k-1}$

#include <iostream>
#include <cstring>
#include <algorithm>

#define x first
#define y second

using namespace std;

typedef pair<int, int> PII;
const int N = 100010;

int n;
PII q[N];
int s[2][N];

int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; i ++ ) scanf("%d%d", &q[i].x, &q[i].y);
    sort(q + 1, q + n + 1);
    for (int i = 0; i < 2; i ++ )
        for (int j = 1; j <= n; j ++ )
            s[i][j] = s[i][j - 1] + (q[j].y == i);

    int cnt = -1, res;
    for (int i = 1; i <= n; i ++ )
    {
        int t = s[0][i - 1] + s[1][n] - s[1][i - 1];
        if (t >= cnt) cnt = t, res = q[i].x;
        while (i + 1 <= n && q[i + 1].x == q[i].x) i ++ ;	// 分界线两侧的数必须不同
    }
    printf("%d\n", res);
    return 0;
}

4.2 二维前缀和

二维前缀和用于求子矩阵的和，运用到的是容斥原理。

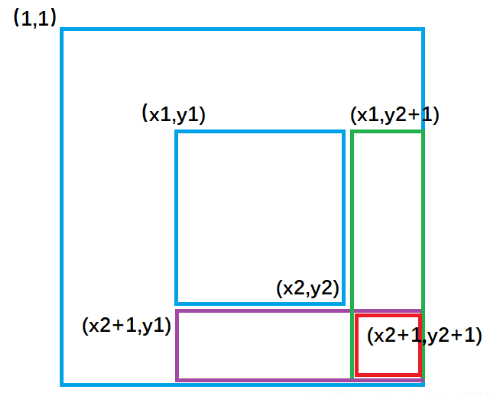
我们先来定义一个二维数组s[][] , s[i][j] 表示二维数组中，左上角(1, 1)到右下角(i, j)所包围的矩阵元素的和。接下来推导二维前缀和的公式。

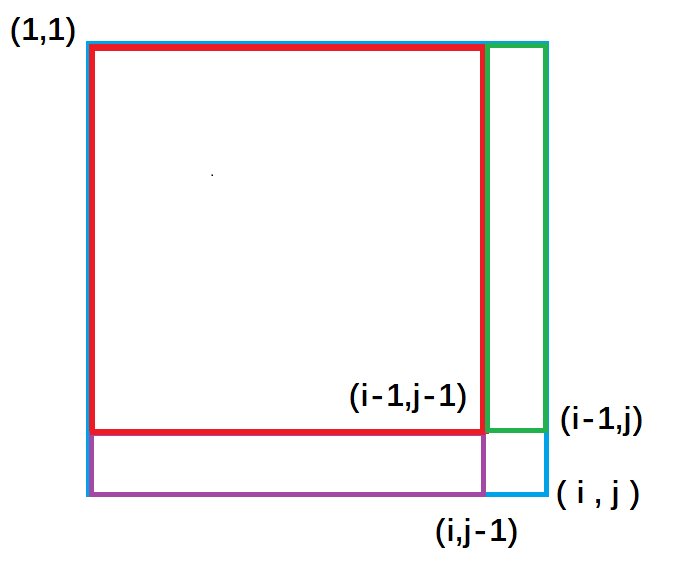
紫色面积是指(1, 1)左上角到(i, j - 1)右下角的矩形面积，绿色面积是指(1, 1)左上角到(i - 1, j)右下角的矩形面积。每一个颜色的矩形面积都代表了它所包围元素的和。

二维前缀和推导1

从图中我们很容易看出，整个外围蓝色矩形面积s[i][j] = 绿色面积s[i - 1][j] + 紫色面积s[i][j - 1] - 重复加的红色的面积s[i - 1][j - 1] + 小方块的面积a[i][j]。

s[i, j] = 第i行j列格子左上部分所有元素的和
s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j]

则我们可以推导出子矩阵的和的公式：

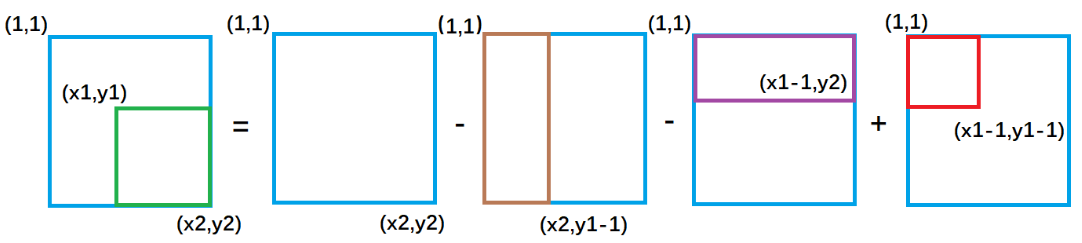
二维前缀和推导2

以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵的和为：

s[x2, y2] - s[x1 - 1, y2] - s[x2, y1 - 1] + s[x1 - 1, y1 - 1]

例1：子矩阵的和

#include<iostream>
const int N = 1010;
using namespace std;

int n, m, q;
int a[N][N], s[N][N];

int main()
{
	scanf("%d%d%d", &n, &m, &q);
	for (int i = 1; i <= n; i++)
		for (int j = 1; j <= m; j++)
			scanf("%d", &a[i][j]);
	for (int i = 1; i <= n; i++)
		for (int j = 1; j <= m; j++)
			//求前缀和
			s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j];
	while (q--)
	{
		int x1, y1, x2, y2;
		scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
		//算子矩阵的和
		printf("%d\n", s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]);
	}
	return 0;
}

例2：邻域均值

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 610;

int n, L, r, t;
int s[N][N];

int get_sum(int x1, int y1, int x2, int y2)
{
    return s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1];
}

int get_cnt(int x1, int y1, int x2, int y2)
{
    return (x2 - x1 + 1) * (y2 - y1 + 1);
}

int main()
{
    scanf("%d%d%d%d", &n, &L, &r, &t);
    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= n; j ++ )
        {
            int x;
            scanf("%d", &x);
            s[i][j] = x + s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];
        }

    int res = 0;
    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= n; j ++ )
        {
            int x1 = max(1, i - r), y1 = max(1, j - r);
            int x2 = min(n, i + r), y2 = min(n, j + r);
            if (get_sum(x1, y1, x2, y2) <= t * get_cnt(x1, y1, x2, y2))
                res ++ ;
        }
    printf("%d\n", res);
    return 0;
}

五、差分

5.1 一维差分

有$a_{1},a_{2},…,a_{n}$[前缀和]，构造$b_{1},b_{2},…,b_{n}$[差分]，使得$a_{i}=b_{1}+b_{2}+…+b_{i}$，则有：

$\begin{cases} b_{1}=a_{1} \ b_{2}= a_{2}-a_{1} \ b_{3}= a_{3}-a_{2} \ … \ b_{n}= a_{n}-a_{n-1} \end{cases}$

O(n)时间由 B 数组得到 A 数组
O(1)时间给 A 数组区间 [l, r] 中的每个数加上 c：B[l] += c, B[r + 1] -= c

例1：差分

#include<iostream>
using namespace std;

const int N = 100010;
int n, m;
int a[N], b[N];

void insert(int l, int r, int c)
{
	b[l] += c;
	b[r + 1] -= c;
}

int main()
{
	scanf("%d%d", &n, &m);
	for (int i = 1; i <= n; i++) {
		scanf("%d", &a[i]);
	}
	for (int i = 1; i <= n; i++) {
		insert(i, i, a[i]);			//将b数组读入值
	}
	while (m--)
	{
		int l, r, c;
		scanf("%d%d%d", &l, &r, &c);
		insert(l, r, c);
	}
	for (int i = 1; i <= n; i++)
		b[i] += b[i - 1];			//前缀和得到"新的a[i]"
	for (int i = 1; i <= n; i++)
		printf("%d ", b[i]);
	return 0;
}

例2：增减序列

给定一个长度为 $n$ 的数列 $a_1,a_2,…,a_n$，每次可以选择一个区间 $[l,r]$，使下标在这个区间内的数都加一或者都减一。

求至少需要多少次操作才能使数列中的所有数都一样，并求出在保证最少次数的前提下，最终得到的数列可能有多少种。

差分数组 b[1] = a[1]，b[2] ~ b[n] = 0，第一问可等价为至少操作多少次，可使 b[2] ~ b[n] 的都为 $0$，第二问可等价为 b[1] 有多少种取值。

$2\leq L\leq R \leq n-1$：在 $b_2$ 至 $b_n$ 中令某一个数加一，另一个数减 $1$（优先，因为改变了 $b_2$ 至 $b_n$ 区间的两个数）
$L= 1,R\leq n-1$：在 $b_1$ 加减 $1$， $b_2$ 至 $b_n$ 的某个数减加 $1$
$2\leq L,R=n$：在 $b_{n+1}$ 加减 $1$， $b_2$ 至 $b_n$ 的某个数减加 $1$
$L = 1,R = n$：无意义

故有：

设 $b_2,b_3,…,b_n$ 中正数总和为 $p$，负数总和的绝对值为 $q$。首先以正负数匹配的方式尽量执行 $1$ 类操作，可执行 $min(p,q)$ 次；剩余 $|p - q|$ 个为待匹配对，每个可以选与 $b_1$ 或 $b_{n + 1}$ 匹配，即执行 $2$ 或 $3$ 类操作，共需 $|p - q|$ 次。故最少操作次数为 $min(p,q) + |p - q| = max(p,q)$；
根据 $|p - q|$ 次第 $2$、$3$ 类操作的选择情况（第 $2$ 类操作执行次数可为 $0,1,…,|p-q|$），能产生 $|p - q| + 1$ 中不同的 $b_1$ 的值，即最终得到的序列 $a$ 可能有 $|p - q| + 1$ 种。

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 100010;

typedef long long LL;

int n;
int a[N], b[N];

int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);
    for (int i = 1; i <= n; i ++ ) b[i] = a[i] - a[i - 1];

    LL p = 0, q = 0;
    // 求正负数总和
    for (int i = 2; i <= n; i ++ )
        if (b[i] > 0) p += b[i];
        else q -= b[i];

    cout << max(p, q) << endl;
    cout << abs(p - q) + 1 << endl;

    return 0;
}

5.2 二维差分

a矩阵是原矩阵，b矩阵是差分矩阵。设a[i][j]是b[i][j]的前缀和，a数组中a[i][j]是b数组左上角(1,1)到右下角(i,j)所包围矩形元素的和。

我们构造二维差分数组目的是为了让原二维数组a中所选中子矩阵中的每一个元素加上c的操作，可以由$O(n^2)$的时间复杂度优化为$O(1)$。

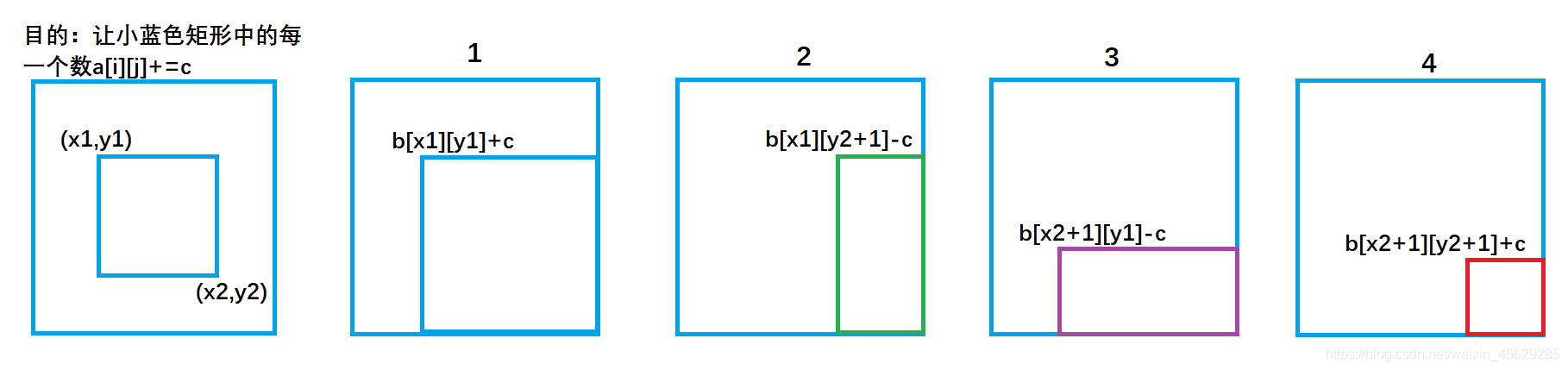
给以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵中的所有元素加上c：
b[x1, y1] += c, b[x2 + 1, y1] -= c, b[x1, y2 + 1] -= c, b[x2 + 1, y2 + 1] += c。

b[x1][y1] += c 对应图1，让整个a数组中蓝色矩形面积的元素都加上了c；
b[x1][y2 + 1] -= c 对应图2，让整个a数组中绿色矩形面积的元素再减去c，使其内元素不发生改变；
b[x2 + 1][y1] -= c对应图3，让整个a数组中紫色矩形面积的元素再减去c，使其内元素不发生改变；
b[x2 + 1][y2 + 1] += c对应图4，让整个a数组中红色矩形面积的元素再加上c，红色内的相当于被减了两次，再加上一次c，才能使其恢复。

操作过程2

例：差分矩阵

#include <iostream>

using namespace std;

const int N = 1010;

int n, m, q;
int a[N][N], b[N][N];

void insert(int x1, int y1, int x2, int y2, int c)
{
    b[x1][y1] += c;
    b[x2 + 1][y1] -= c;
    b[x1][y2 + 1] -= c;
    b[x2 + 1][y2 + 1] += c;
}

int main()
{
    scanf("%d%d%d", &n, &m, &q);

    // 读取a[i][j]矩阵的值
    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
            scanf("%d", &a[i][j]);

    // 插入每个数
    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
            insert(i, j, i, j, a[i][j]);

    // 进行q次操作
    while (q -- )
    {
        int x1, y1, x2, y2, c;
        cin >> x1 >> y1 >> x2 >> y2 >> c;
        insert(x1, y1, x2, y2, c);
    }

    // 求前缀和
    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
            b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];

    for (int i = 1; i <= n; i ++ )
    {
        for (int j = 1; j <= m; j ++ ) printf("%d ", b[i][j]);
        puts("");
    }

    return 0;
}

六、双指针算法

Case1：对于两个序列，维护某种次序：

如在归并排序中合并两个有序序列的操作：两个指针分别位于数组相应的位置，依次向右遍历，当数组执行到尾部，合并完成。

Case2：对于一个序列，用两个指针维护一段区间：

如快排，两个指针分别位于左右两端，依次中间比较交换。

for(i = 0, j = 0; i < n; i++)
{
	while(j < i && check(i, j)) j ++;		// 寻找i, j的单调关系
    // 每道题的具体逻辑
}

核心思想：将for(int i = 0; i < n; i++) for(int j = 0; j < n; j++)朴素算法的时间复杂度优化到O(n)。

[例：给定一个字符串，进行分割]

#include<iostream>
#include<string.h>

using namespace std;

int main()
{
	char str[1000];
	gets(str);
	int n = strlen(str);
	for (int i = 0; i < n; i++)
	{
		int j = i;
		while (j < n && str[j] != ' ') j++;
		// 这道题具体逻辑
		for (int k = i; k < j; k++)
		{
			cout << str[k];
		}
		cout << endl;
		i = j;
	}
}

例：最长连续不重复子序列

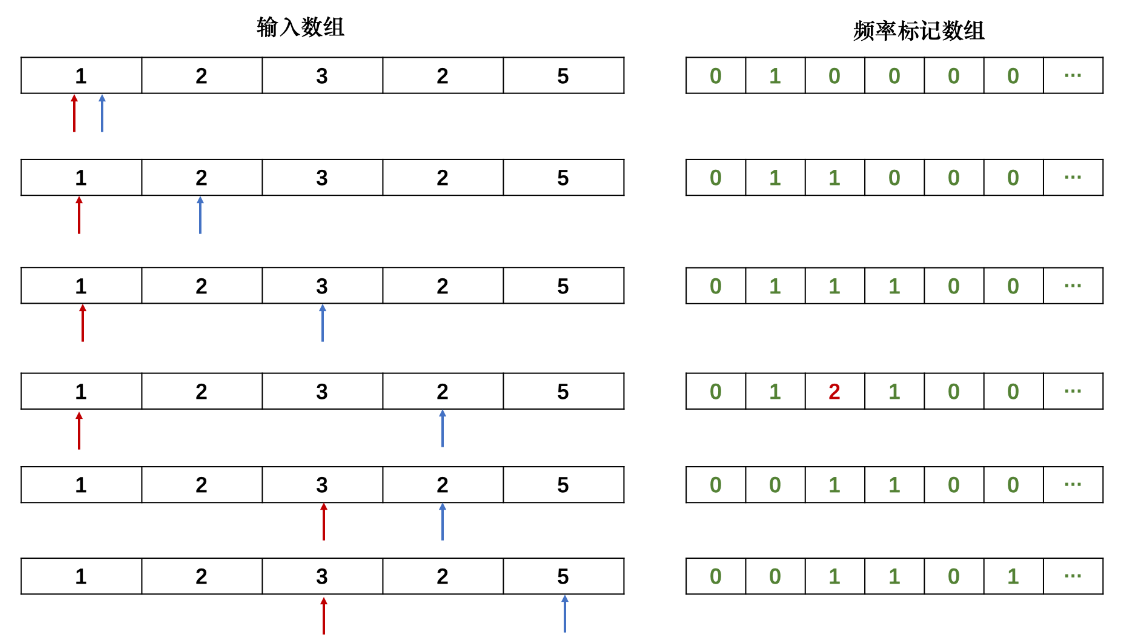
// 双指针算法:O(n)
for (int i = 0, j = 0; i < n; i++)
{
	while (j <= i && check(j, i)) j++;		// j往左最远能到什么地方
	res = max(res, i - j + 1);
}

#include <iostream>
using namespace std;

const int N = 100010;

int n;
int a[N],s[N];

int main()
{
    cin >> n;
    for (int i = 0; i < n; i ++ ) cin >> a[i];

    int res = 0;
    for (int i = 0, j = 0; i < n; i ++ )
    {
        s[a[i]] ++ ;
        // j 往左走最远能到什么地方
        while (s[a[i]] > 1)
        {
            s[a[j]] -- ;
            j ++ ;
        }
        res = max(res, i - j + 1);
    }

    cout << res << endl;

    return 0;
}

七、位运算

7.1 n的二进制表示第k位

n的二进制表示中第k位是几($k={0,1,2,…,n}$)

先把第k位移到最后一位，n>>k
看个位是几，x && 1

即n>>k & 1

7.2 lowbit

lowbit(x)：返回x的最后一位1是多少，是树状数组的基本操作。

x=1010，lowbit(x)=10

x=101000，lowbit(x)=1000

例：二进制中1的个数

#include<iostream>
using namespace std;

int lowbit(int x)
{
	return x & -x;
}

int main()
{
	int n;
	cin >> n;
	while (n--)
	{
		int x;
		cin >> x;
		int res = 0;
		while (x)
		{
			x -= lowbit(x);
			res++;		//每次减去x的最后一位1
		}
		cout << res << " ";
	}
	return 0;
}

八、离散化

值域$0-10^{9}$，个数$10^{5}$

a[]:1、3、100、2000、500000映射为0、1、2、3、4。

问题：

a[]中可能有重复元素—–>去重
如何算出x离散化后的值—–>二分

vector<int> alls; 		// 存储所有待离散化的值
sort(alls.begin(), alls.end()); 	// 将所有值排序
alls.erase(unique(alls.begin(), alls.end()), alls.end());   // 去掉重复元素

// 二分求出x对应的离散化的值
int find(int x) 		// 找到第一个大于等于x的位置
{
    int l = 0, r = alls.size() - 1;
    while (l < r)
    {
        int mid = l + r >> 1;
        if (alls[mid] >= x) r = mid;
        else l = mid + 1;
    }
    return r + 1;	 	// 映射到1, 2, ...n
}

例：区间和

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

typedef pair<int, int> PII;

const int N = 300010;

int n, m;
int a[N], s[N];

vector<int> alls;
vector<PII> add, query;

int find(int x)
{
    int l = 0, r = alls.size() - 1;
    while (l < r)
    {
        int mid = l + r >> 1;
        if (alls[mid] >= x) r = mid;
        else l = mid + 1;
    }
    return r + 1;
}

int main()
{
    cin >> n >> m;
    for (int i = 0; i < n; i ++ )
    {
        int x, c;
        cin >> x >> c;
        add.push_back({x, c});

        alls.push_back(x);
    }

    for (int i = 0; i < m; i ++ )
    {
        int l, r;
        cin >> l >> r;
        query.push_back({l, r});

        alls.push_back(l);
        alls.push_back(r);
    }

    // 去重
    sort(alls.begin(), alls.end());
    alls.erase(unique(alls.begin(), alls.end()), alls.end());

    // 处理插入
    for (auto item : add)
    {
        int x = find(item.first);
        a[x] += item.second;
    }

    // 预处理前缀和
    for (int i = 1; i <= alls.size(); i ++ ) s[i] = s[i - 1] + a[i];

    // 处理询问
    for (auto item : query)
    {
        int l = find(item.first), r = find(item.second);
        cout << s[r] - s[l - 1] << endl;
    }

    return 0;
}

[注]unique函数实现方法：

vector<int>::iterator unique(vector<int> &a)
{
 int j = 0;
 for(int i = 0;i < a.size();i++)
 {
     if(!i || a[i] != a[i-1])	//若其为第一个元素或其与前一个元素不相同
         a[j++] = a[i];
 }
 // a[0] - a[j-1]	所有a中不重复的数
 return a.begin() + j;
}

九、区间合并

按区间左端点进行排序，则区间与现有维护区间仅存在以下三种情况：

区间合并

Case1：现有维护区间不变
Case2：ed更新
Case3：由于按左端点进行排序，两个区间没有交集，则现有维护区间不会发生改变，可以直接放入答案中，然后将维护区间更新成现在的st和ed

// 将所有存在交集的区间合并
void merge(vector<PII> &segs)
{
    vector<PII> res;

    sort(segs.begin(), segs.end());			 // 将所有区间排序

    int st = -2e9, ed = -2e9;				// 2*10的九次方
    for (auto seg : segs)
    {
        if (ed < seg.first)					// 第三种情况即找到新区间
        {
            if (st != -2e9) res.push_back({st, ed});
            st = seg.first, ed = seg.second;
        }
        else ed = max(ed, seg.second);		 // 右端点更新
    }

    if (st != -2e9) res.push_back({st, ed});  // 将最后一个区间加入答案,st != -2e9防止空区间

    segs = res;
}

Java 写法：

class Solution {
    public int[][] merge(int[][] intervals) {
        /*
        贪心策略:
        1.按照左边界升序排序
        2.当intervals[i][0]<=intervals[i-1][1]时,说明能合并,更新intervals[i][1]=max(intervals[i][1],intervals[i-1][1])
        3.当intervals[i][0]>intervals[i-1][1]时,区间不重叠,将前面区间加入结果,更新新的左边界
        4.理论上最后一个结果不会加人,手动加入即可
         */
        List<int[]> list = new ArrayList<>();
        Arrays.sort(intervals, Comparator.comparingInt(a -> a[0]));
        // 每个重叠区间组左边界
        var len = intervals.length;
        int start = intervals[0][0];
        for (int i = 1; i < len; i++) {
            if (intervals[i][0] > intervals[i - 1][1]) {
                list.add(new int[]{start, intervals[i - 1][1]});
                // 更新区间组起点
                start = intervals[i][0];
            } else {
                // 更新区间组最大值,表示该区间组合并后的右边界
                intervals[i][1] = Math.max(intervals[i][1], intervals[i - 1][1]);
            }
        }
        // 添加最后一个区间(这使得区间数目为1也成立)
        list.add(new int[]{start, intervals[len - 1][1]});
        return list.toArray(new int[0][]);
    }
}

ShiQuLiZhi

https://www.qqzzss.top/2022/08/13/algorithmlearning/suan-fa-01-ji-chu-suan-fa/

本博客所有文章除特别声明外，均采用 CC BY 4.0 许可协议。转载请注明来源 ShiQuLiZhi !

算法数据结构

算法2:数据结构

2022-08-13 算法学习

算法数据结构

JDBC

2022-08-13 Java与开发基础

数据库 Web技术

算法1:基础算法

一、排序算法

1.1 快速排序

1.2 归并排序

二、二分算法

2.1 整数二分算法

2.2 浮点数二分算法

三、高精度

3.1 高精度加法

3.2 高精度减法

3.3 高精度乘法

3.3.1 高精度乘低精度

3.3.2 高精度乘高精度

3.4 高精度除以低精度

四、前缀和

4.1 一维前缀和

4.2 二维前缀和

五、差分

5.1 一维差分

5.2 二维差分

六、双指针算法

七、位运算

7.1 n的二进制表示第k位

7.2 lowbit

八、离散化

九、区间合并