一、背包问题
- 0/1背包:每类物品最多只能装一次
- 完全背包:物品无限量
- 多重背包:每类物品有个数限制,第 $i$ 类物品有 $num[i]$ 个
- 分组背包:每组物品有若干个,同一组内的物品最多只能选一个
1.1 0/1背包
有 $N$ 件物品和一个容量是 $V$ 的背包。每件物品只能使用一次。
**第 $i$ 件物品的体积是 $v_{i}$,价值是 $w_{i}$**。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。输出最大价值。
DP问题:
- 状态表示$f(i,j)$:
- 集合
- 所有选法
- 条件:(1)只从前 $i$ 个物品中选; (2)总体积$\leq j$
- 属性:$Max$(✔), $Min$, 数量
- 集合
- 状态计算:集合划分——$f(i,j)$
- 不含 $i$:$f(i-1,j)$
- 含 $i$:$f(i-1,j-v_i)+w_i$
故有:$f(i,j) = Max(f(i-1,j),f(i-1,j-v_i)+w_i)$
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N][N];
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];
for(int i = 1; i <= n; i++)
{
for(int j = 0; j <= m; j++)
{
f[i][j] = f[i - 1][j];
if(j >= v[i]) f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);
}
}
cout << f[n][m] << endl;
return 0;
}优化为一维的方法:需逆序
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N];
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];
for (int i = 1; i <= n; i ++ )
for (int j = m; j >= v[i]; j -- )
f[j] = max(f[j], f[j - v[i]] + w[i]); // 1
cout << f[m] << endl;
return 0;
}注:(1式)
f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);若改为一维(滚动数组),且
j从v[i]开始递增,则算到第i层时,f[j - v[i]]已经被更新为第i层的,不符合二维情况,故j应递减遍历。
1.2 完全背包
有 $N$ 件物品和一个容量是 $V$ 的背包,每件物品都有无限件可用。
**第 $i$ 件物品的体积是 $v_{i}$,价值是 $w_{i}$**。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。输出最大价值。
DP问题:
状态表示$f(i,j)$:
- 集合
- 所有选法
- 条件:(1)只从前 $i$ 个物品中选; (2)总体积$\leq j$
- 属性:$Max$
- 集合
状态计算:集合划分——$f(i,j)$
曲线救国:
- 去掉 $k$ 个物品 $i$
- 求 $Max$,$f[i - 1,j - k * v[i]]$
- 再加回来 $k$ 个物品 $i$
以物品 $i$ 选的数量进行集合划分:
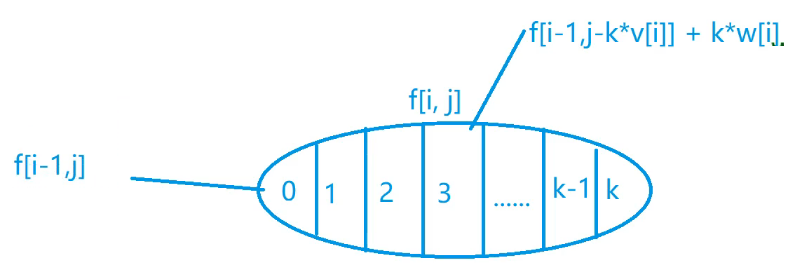
故有:$f[i,j] = f[i - 1,j - k * v[i]] + k * w[i]$
朴素做法(枚举k):
for (int i = 1; i <= n; i++)
{
for (int j = 0; j <= m; j++)
{
for (int k = 0; k * v[i] <= j; k++)
{
f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
}
}
}优化做法:
由动态规划的转移方程入手。观察以下式子:
$f[i,j]=Max(f[i-1,j],f[i-1,j-v]+w,f[i-1,j-2v]+2w,f[i-1,j-3v]+3w,…)$
$f[i,j-v]=Max(\quad\quad\quad f[i-1,j-v],f[i-1,j-2v]+w,f[i-1,j-3v]+2w,…)$
两式从第二项开始只差了 w,故可得$f[i-1,j-v]+w,f[i-1,j-2v]+2w,f[i-1,j-3v]+3w,…$的最大值为 $f[i,j-v]+w$
故**不需要枚举所有 k**,只需求以下两式即可:$f[i,j]=Max(f[i-1,j],f[i,j-v]+w)$
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N];
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];
for (int i = 1; i <= n; i ++ )
for (int j = v[i]; j <= m; j ++ )
f[j] = max(f[j], f[j - v[i]] + w[i]);
cout << f[m] << endl;
return 0;
}1.3 多重背包
有$N$件物品和一个容量是$V$的背包。每件物品都有无限件可用。
**第 $i$ 种物品最多有 $s_i$ 件,每件体积是 $v_{i}$,价值是 $w_{i}$**。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。输出最大价值。
DP问题:
- 状态表示$f(i,j)$:
- 集合
- 所有选法
- 条件:(1)只从前$i$个物品中选; (2)总体积$\leq j$
- 属性:$Max$
- 集合
- 状态计算:集合划分——$f(i,j)$
朴素做法(枚举k):
$f(i,j) = Max(f(i-1,j-v[i]*k)+w[i]*k)(k=0,1,2,…,s[i])$
for (int i = 1; i <= n; i ++ )
for (int j = 0; j <= m; j ++ )
for (int k = 0; k <= s[i] && k * v[i] <= j; k ++ )
f[i][j] = max(f[i][j], f[i - 1][j - v[i] * k] + w[i] * k);优化做法:二进制的优化方式(与快速幂的原理类似)
如$s=1024$,不需要列举$s$从0到1023的所有情况,只需列举$s$有1,2,4,8,…,512件的情况,则0-1023内的所有情况都能由上述情况表示,等价于一个01背包问题。
对于一个一般的$s$,有:$1,2,4,…,2^k,c(c<2^{k+1})$
$s\rightarrow logs$,再对新的物品做一遍01背包问题即可。
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 12010, M = 2010;
int n, m;
int v[N], w[N];
int f[M];
int main()
{
cin >> n >> m;
int cnt = 0;
for (int i = 1; i <= n; i ++ )
{
int a, b, s;
cin >> a >> b >> s;
int k = 1;
while (k <= s)
{
cnt ++ ;
v[cnt] = a * k;
w[cnt] = b * k;
s -= k;
k *= 2;
}
if (s > 0)
{
cnt ++ ;
v[cnt] = a * s;
w[cnt] = b * s;
}
}
n = cnt;
//做一个01背包问题即可
for (int i = 1; i <= n; i ++ )
for (int j = m; j >= v[i]; j -- )
f[j] = max(f[j], f[j - v[i]] + w[i]);
cout << f[m] << endl;
return 0;
}1.4 分组背包
有 $N$ 组物品和一个容量是 $V$ 的背包。
每组物品有若干个,同一组内的物品最多只能选一个。
每件物品的体积是 $v_{ij}$,价值是 $w_{ij}$,其中 $i$ 是组号,$j$ 是组内编号。
求解将哪些物品装入背包,可使物品总体积不超过背包容量,且总价值最大。输出最大价值。
DP问题:
- 状态表示$f(i,j)$:
- 集合
- 所有选法
- 条件:(1)只从前 $i$ 组物品中选; (2)总体积$\leq j$
- 属性:$Max$
- 集合
- 状态计算:集合划分——$f(i,j)$
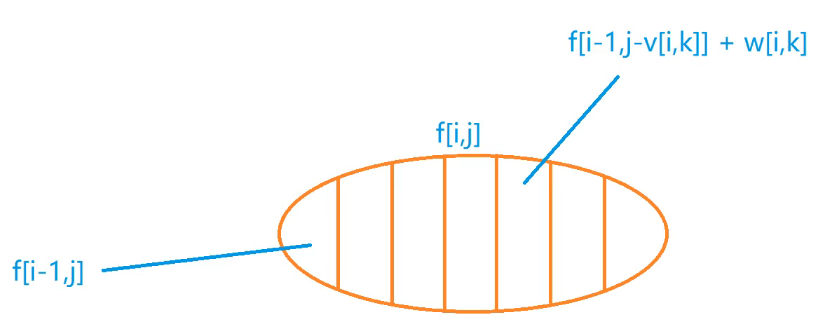
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 110;
int n, m;
int v[N][N], w[N][N], s[N];
int f[N];
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i ++ )
{
cin >> s[i];
for (int j = 0; j < s[i]; j ++ )
cin >> v[i][j] >> w[i][j];
}
for (int i = 1; i <= n; i ++ )
for (int j = m; j >= 0; j -- )
for (int k = 0; k < s[i]; k ++ )
if (v[i][k] <= j)
f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);
cout << f[m] << endl;
return 0;
}二、线性DP
2.1 数字三角形模型
2.1.1 基本问题
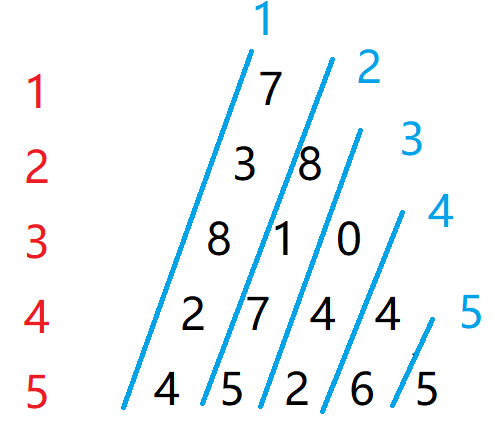
给定一个如下图所示的数字三角形,从顶部出发,在每一结点可以选择移动至其左下方的结点或移动至其右下方的结点,一直走到底层,要求找出一条路径,使路径上的数字的和最大。
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5DP问题:
状态表示$f(i,j)$:
集合
所有从起点走到 $(i,j)$ 的路径
属性:$Max$
状态计算:集合划分——$f(i,j)$
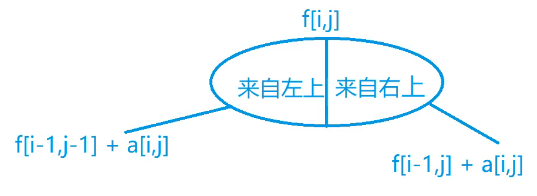
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 510, INF = 1e9;
int n;
int a[N][N]; // 存每一层第几个点
int f[N][N];
int main()
{
scanf("%d", &n);
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= i; j ++ )
scanf("%d", &a[i][j]);
for (int i = 0; i <= n; i ++ )
for (int j = 0; j <= i + 1; j ++ ) // 1
f[i][j] = -INF;
f[1][1] = a[1][1];
for (int i = 2; i <= n; i ++ )
for (int j = 1; j <= i; j ++ )
f[i][j] = max(f[i - 1][j - 1] + a[i][j], f[i - 1][j] + a[i][j]);
int res = -INF;
for (int i = 1; i <= n; i ++ ) res = max(res, f[n][i]); // 枚举最后一层元素
printf("%d\n", res);
return 0;
}注:
for (int j = 0; j <= **i + 1**; j ++ ) —–> 每次需多初始化一个元素
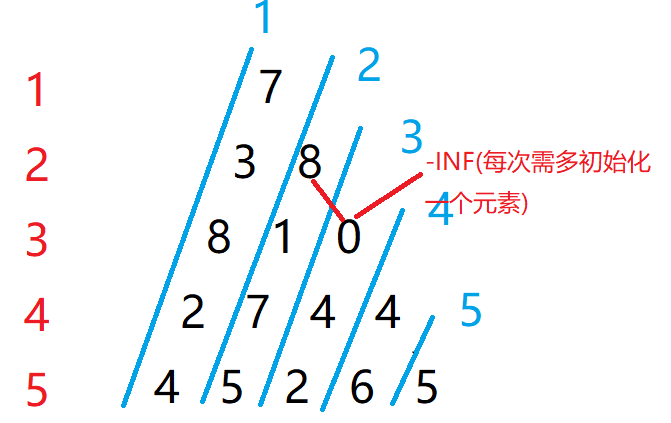
2.1.2 变式1:摘花生
Hello Kitty想摘点花生送给她喜欢的米老鼠。
她来到一片有网格状道路的矩形花生地(如下图),从西北角进去,东南角出来。
地里每个道路的交叉点上都有种着一株花生苗,上面有若干颗花生,经过一株花生苗就能摘走该它上面所有的花生。
Hello Kitty只能向东或向南走,不能向西或向北走。
问Hello Kitty最多能够摘到多少颗花生。
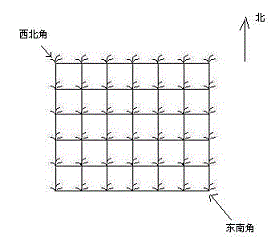
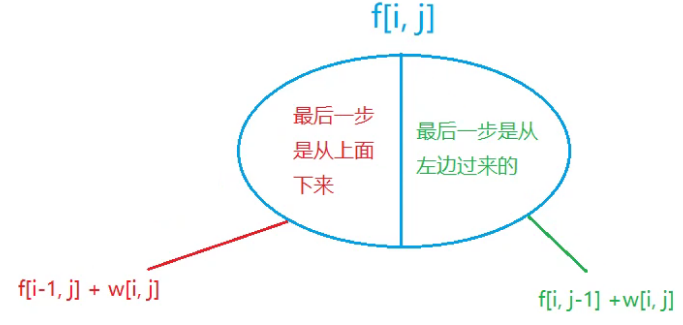
从集合角度来考虑DP问题:
状态表示$f(i,j)$:
- 集合:所有从$(1,1)$走到$(i,j)$的路线
- 属性:$Max$
状态计算:集合划分——$f(i,j)$
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 110;
int n, m;
int w[N][N];
int f[N][N];
int main()
{
int T;
scanf("%d", &T);
while (T -- )
{
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
scanf("%d", &w[i][j]);
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
f[i][j] = max(f[i - 1][j], f[i][j - 1]) + w[i][j];
printf("%d\n", f[n][m]);
}
return 0;
}2.1.3 变式2:方格取数
设有 $N×N$ 的方格图,我们在其中的某些方格中填入正整数,而其它的方格中则放入数字0。如下图所示:
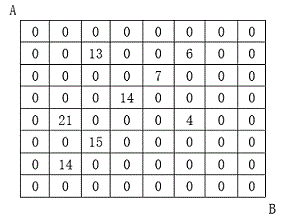
某人从图中的左上角 $A$ 出发,可以向下行走,也可以向右行走,直到到达右下角的 $B$ 点。
在走过的路上,他可以取走方格中的数(取走后的方格中将变为数字0)。
此人从 $A$ 点到 $B$ 点共走了两次,试找出两条这样的路径,使得取得的数字和为最大。
DP问题:
状态表示$f(i_1,j_1,i_2,j_2)$:表示所有从$(1,1),(1,1)$分别走到$(i_1,j_1),(i_2,j_2)$的路径的最大值
如何处理“同一个格子不能被重复选择”:
只有在$i_1+j_1==i_2+j_2$(走的步数相同)时,两条路径的格子才可以重合
故可以优化状态:$f(k,i_1,i_2)$表示所有从$(1,1),(1,1)$分别走到$(i_1,k-i_1),(i_2,k-i_2)$的路径的最大值,其中 $k$ 表示两条路线当前走到的格子的横纵坐标之和,$k=i_1+j_1=i_2+j_2$
我们要做的是若格子有重合,该格子的值仅被计算一次
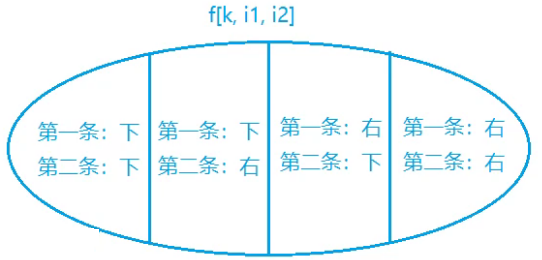
状态计算:
以第一种情况为例:
第一条的轨迹为$(1,1)\rightarrow (i_1-1,j_1)\rightarrow (i_1,j_1)$
第二条的轨迹为$(1,1)\rightarrow (i_2-1,j_2)\rightarrow (i_2,j_2)$
$f(k,i_1,i_2) = Max; f(k-1,i_1-1,i_2-1)=\begin{cases}重合:w(i_1,j_1)\不重合:w(i_1,j_1)+w(i_2,j_2)\end{cases}$
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 15;
int n;
int w[N][N];
int f[N * 2][N][N];
int main()
{
scanf("%d", &n);
int a, b, c;
while (cin >> a >> b >> c, a || b || c) w[a][b] = c;
for (int k = 2; k <= n + n; k ++ )
for (int i1 = 1; i1 <= n; i1 ++ )
for (int i2 = 1; i2 <= n; i2 ++ )
{
int j1 = k - i1, j2 = k - i2;
if (j1 >= 1 && j1 <= n && j2 >= 1 && j2 <= n)
{
int t = w[i1][j1];
if (i1 != i2) t += w[i2][j2];
int &x = f[k][i1][i2];
x = max(x, f[k - 1][i1 - 1][i2 - 1] + t);
x = max(x, f[k - 1][i1 - 1][i2] + t);
x = max(x, f[k - 1][i1][i2 - 1] + t);
x = max(x, f[k - 1][i1][i2] + t);
}
}
printf("%d\n", f[n + n][n][n]);
return 0;
}2.2 最长上升子序列问题(LIS问题)
2.2.1 基本问题
例2:最长上升子序列(Longest Increasing Subsequence)
给定一个长度为 $N$ 的数列,求数值严格单调递增的子序列的长度最长是多少。
7
3 1 2 1 8 5 6答案是4($[1,2,5,6]$)。
DP问题:
状态表示$f(i)$:
- 集合:所有以第 $i$ 个数结尾的上升子序列
- 属性:$Max$
状态计算:集合划分——$f(i)$
划分依据:最后一个不同的点

以上一个数的位置进行划分(0表示没有上一个数,序列长度为1)
若$a_j<a_i$,则$f[i] = max(f[j] + 1),j=0,1,2,…,i-1$
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n;
int a[N], f[N];
int main()
{
scanf("%d", &n);
for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);
for (int i = 1; i <= n; i ++ )
{
f[i] = 1; // 只有a[i]一个数
for (int j = 1; j < i; j ++ )
if (a[j] < a[i])
f[i] = max(f[i], f[j] + 1);
}
int res = 0;
for (int i = 1; i <= n; i ++ ) res = max(res, f[i]);
printf("%d\n", res);
return 0;
}时间复杂度为$O(n^2)$
存储每种长度的上升子序列的最后一位最小是多少。随着长度的增加,最长上升子序列的最后一位值是严格单调递增的。
证明:不妨设长度为$x$的最长上升子序列最后一位与长度为$x-1$的相同,则长度为$x$的子序列的倒数第二位必然比最后一位小,故找到一个长度为$x-1$的最长上升子序列,使得其最后一位更小,与前提矛盾。
我们找到一个最大的小于$a[i]$的数,如$q[4]$,则$q[5]\geq a[i]$,则$a[i]$无法接到长度大于等于5的上升子序列的后面,因此以$a[i]$结尾的最大上升子序列为5,并将 $q[5]$ 的值更新。
时间复杂度为$O(nlogn)$( $logn$ 为二分查找的时间复杂度)
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010;
int n;
int a[N];
int q[N];
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; i ++ ) scanf("%d", &a[i]);
int len = 0; // q数组中的元素个数
for (int i = 0; i < n; i ++ ) // 枚举每个数
{
int l = 0, r = len;
while (l < r)
{
int mid = l + r + 1 >> 1; // l = mid,故上取整
if (q[mid] < a[i]) l = mid;
else r = mid - 1;
}
len = max(len, r + 1); // r + 1代表接到哪个位置的后面
q[r + 1] = a[i]; // q[r]是小于a[i]的最后一个数, q[r + 1] >= a[i]
}
printf("%d\n", len);
return 0;
}2.2.2 变式1:怪盗基德的滑翔翼
假设城市中一共有 $N$ 幢建筑排成一条线,每幢建筑的高度各不相同。
初始时,怪盗基德可以在任何一幢建筑的顶端。
他可以选择一个方向逃跑,但是不能中途改变方向(因为中森警部会在后面追击)。
因为滑翔翼动力装置受损,他只能往下滑行(即:只能从较高的建筑滑翔到较低的建筑)。
他希望尽可能多地经过不同建筑的顶部,这样可以减缓下降时的冲击力,减少受伤的可能性。
请问,他最多可以经过多少幢不同建筑的顶部(包含初始时的建筑)?
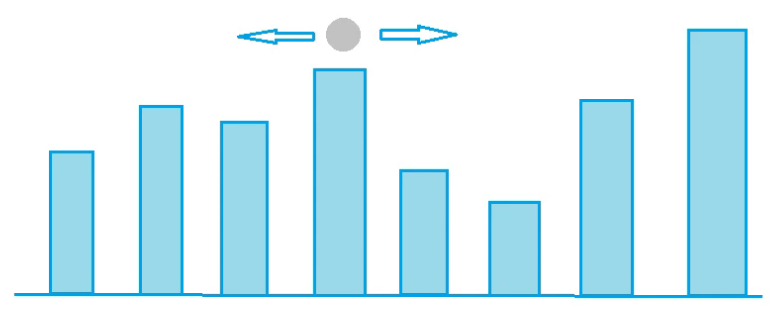
问题核心:当确定完方向和起点后,最长的距离是什么?
起点:$a[i]$
最长距离:以$a[i]$结尾的最长上升子序列(包括从左向右/从右向左)
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 110;
int n;
int h[N];
int f[N];
int main()
{
int T;
scanf("%d", &T);
while (T -- )
{
scanf("%d", &n);
for (int i = 0; i < n; i ++ ) scanf("%d", &h[i]);
int res = 0;
// 正向求解LIS问题
for (int i = 0; i < n; i ++ )
{
f[i] = 1;
for (int j = 0; j < i; j ++ )
if (h[i] < h[j])
f[i] = max(f[i], f[j] + 1);
res = max(res, f[i]);
}
memset(f, 0, sizeof f);
// 反向求解LIS问题
for (int i = n - 1; i >= 0; i -- )
{
f[i] = 1;
for (int j = n - 1; j > i; j -- )
if (h[i] < h[j])
f[i] = max(f[i], f[j] + 1);
res = max(res, f[i]);
}
printf("%d\n", res);
}
return 0;
}2.2.3 变式2:登山
五一到了,ACM队组织大家去登山观光,队员们发现山上一共有N个景点,并且决定按照顺序来浏览这些景点,即每次所浏览景点的编号都要大于前一个浏览景点的编号。
同时队员们还有另一个登山习惯,就是不连续浏览海拔相同的两个景点,并且一旦开始下山,就不再向上走了。
队员们希望在满足上面条件的同时,尽可能多的浏览景点,你能帮他们找出最多可能浏览的景点数么?
条件1:按照编号递增的顺序来浏览 —> 必须是子序列
条件2:相邻两个景点不能相同
条件3:一旦开始下降,就不能上升了 —> 路线形状先严格上升再严格下降
目标:所有形状是该形状的子序列长度的最大值
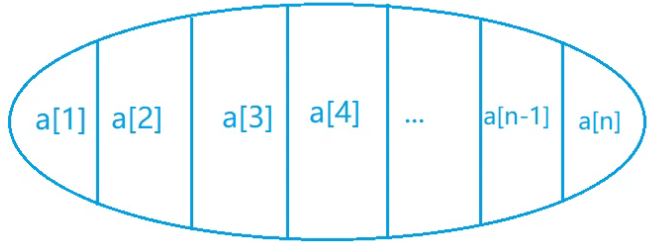
$res=f[i]+g[i]-1$
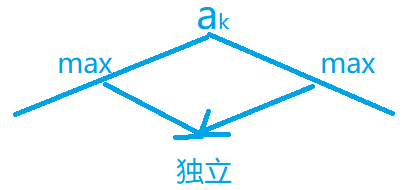
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n;
int h[N];
int f[N], g[N];
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; i ++ ) scanf("%d", &h[i]);
for (int i = 0; i < n; i ++ )
{
f[i] = 1;
for (int j = 0; j < i; j ++ )
if (h[i] > h[j])
f[i] = max(f[i], f[j] + 1);
}
for (int i = n - 1; i >= 0; i -- )
{
g[i] = 1;
for (int j = n - 1; j > i; j -- )
if (h[i] > h[j])
g[i] = max(g[i], g[j] + 1);
}
int res = 0;
for (int i = 0; i < n; i ++ ) res = max(res, f[i] + g[i] - 1);
printf("%d\n", res);
return 0;
}2.2.4 变式3:友好城市
某国有一条横贯东西的大河,河有笔直的南北两岸,岸上各有位置各不相同的 $N$ 个城市。北岸的每个城市有且仅有一个友好城市在南岸,而且不同城市的友好城市不相同。
每对友好城市都向政府申请在河上开辟一条直线航道连接两个城市,但是由于河上雾太大,政府决定避免任意两条航道交叉,以避免事故。
编程帮助政府做出一些批准和拒绝申请的决定,使得在保证任意两条航线不相交的情况下,被批准的申请尽量多。
条件1:每个城市上只能建立一座桥
条件2:所有的桥与桥之间不能相交
目标:最多可以建多少桥?
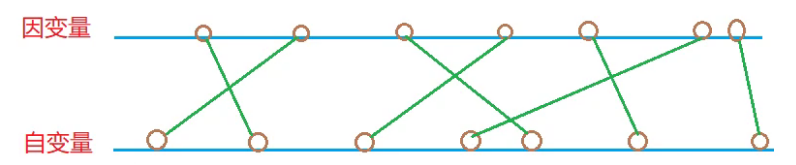
按照自变量的大小排序,然后在因变量中求解上升子序列即可。
#include <iostream>
#include <algorithm>
using namespace std;
typedef pair<int, int> PII;
const int N = 5010;
int n;
PII city[N];
int f[N];
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; i ++ ) scanf("%d%d", &city[i].first, &city[i].second);
sort(city, city + n);
int res = 0;
for (int i = 0; i < n; i ++ )
{
f[i] = 1;
for (int j = 0; j < i; j ++ )
if (city[i].second > city[j].second)
f[i] = max(f[i], f[j] + 1);
res = max(res, f[i]);
}
printf("%d\n", res);
return 0;
}2.2.5 变式4:拦截导弹
某国为了防御敌国的导弹袭击,发展出一种导弹拦截系统。
但是这种导弹拦截系统有一个缺陷:虽然它的第一发炮弹能够到达任意的高度,但是以后每一发炮弹都不能高于前一发的高度。
某天,雷达捕捉到敌国的导弹来袭。
由于该系统还在试用阶段,所以只有一套系统,因此有可能不能拦截所有的导弹。
输入导弹依次飞来的高度(雷达给出的高度数据是不大于30000的正整数,导弹数不超过1000),计算这套系统最多能拦截多少导弹,如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。
选择1:接在现有的某个子序列之后
选择2:创建1个新系统
贪心流程:从前往后扫描每个数,对于每个数:
- 情况1:如果现有的子序列的结尾都小于当前数,则创建新子序列
- 情况2:将当前数放到结尾大于等于它的最小的子序列后面
我们证明贪心算法的正确性:
$A$ 表示贪心算法得到的序列个数,$B$ 表示最优解
由于是最优解,必然存在 $B<=A$ ,接下来证明 $A<=B$,运用调整法:
假设存在一种最优策略,不是按照贪心方案进行阶段决策的,如下图,则最优解序列与贪心法得到的序列不同的数存在关系 $b\geq a$,我们可以通过有限次的调整,把最优解调整成贪心解的方案,且不增加子序列个数。
故最优解得到的序列个数小于等于贪心算法得到的序列个数。综上,贪心解即是最优解。
#include <sstream>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n;
int h[N], f[N], q[N];
int main()
{
while (cin >> h[n]) n ++ ;
int res = 0, cnt = 0;
for (int i = 0; i < n; i ++ )
{
f[i] = 1;
for (int j = 0; j < i; j ++ )
if (h[i] <= h[j])
f[i] = max(f[i], f[j] + 1);
res = max(res, f[i]);
int k = 0;
while (k < cnt && q[k] < h[i]) k ++ ; // q数组将是单调上升的,注1
if (k == cnt) q[cnt ++ ] = h[i];
else q[k] = h[i];
}
printf("%d\n", res);
printf("%d\n", cnt);
return 0;
}注:
假设 $q$ 数组原先是单调上升的,有$c\leq a \leq b$,而假设 $x$ 要替换 $a$ 这个位置中,则有$c<x\leq a \leq b$,替换后有$c<x \leq b$,仍是单调上升的。
也即,$q$ 数组成立条件是现有的结尾元素都比当前值 $a[i]$ 小 才会创建新的序列,所以 $q$ 排序一定是从小到大的,这样顺序查找就相当于 $\geq a[i]$ 的最小的元素。
2.2.6 变式5:导弹防御系统
为了对抗附近恶意国家的威胁,$R$ 国更新了他们的导弹防御系统。
一套防御系统的导弹拦截高度要么一直 严格单调 上升要么一直 严格单调 下降。
例如,一套系统先后拦截了高度为 $3$ 和高度为 $4$ 的两发导弹,那么接下来该系统就只能拦截高度大于 $4$ 的导弹。
给定即将袭来的一系列导弹的高度,请你求出至少需要多少套防御系统,就可以将它们全部击落。
暴力搜索
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 55;
int n;
int q[N];
int up[N], down[N];
int ans;
void dfs(int u, int su, int sd) {
if (su + sd >= ans) return; // ans不可能再小了
if (u == n) {
ans = su + sd; // su, sd 分别表示 len(up[]), len(down[])
return;
}
// 情况1:将当前数放到上升子序列中
int k = 0;
while (k < su && up[k] >= q[u]) k ++;
int t = up[k];
up[k] = q[u];
if (k < su) dfs(u + 1, su, sd);
else dfs(u + 1, su + 1, sd);
up[k] = t;
// 情况2:将当前数放到下降子序列中。
k = 0;
while (k < sd && down[k] <= q[u]) k ++;
t = down[k];
down[k] = q[u];
if (k < sd) dfs(u + 1, su, sd);
else dfs(u + 1, su, sd + 1);
down[k] = t;
}
int main()
{
while (cin >> n, n) {
for (int i = 0; i < n; i ++)
cin >> q[i];
ans = n;
dfs(0, 0, 0);
cout << ans << endl;
}
}2.3 最长公共子序列问题(LCS问题)
给定两个长度分别为 $N$ 和 $M$ 的字符串 $A$ 和 $B$,求既是 $A$ 的子序列又是 $B$ 的子序列的字符串长度最长是多少。
4 5
acbd
abedc输出为3。
DP问题:
状态表示$f(i,j)$:
- 集合
- 所有在第一个序列的前$i$个字母中出现,且在第二个序列的前$j$个字母中出现的子序列
- 属性:$Max$
- 集合
状态计算:
集合划分——$f(i,j)$
以$a[i],b[j]$是否出现进行划分:

注:
$f(i-1,j)$包含01情况,可以直接以其作为代表;
$f(i-1,j)$和$f(i,j-1)$包含00情况$f(i-1,j-1)$,则可以不计算$f(i-1,j-1)$.
规划方程:$c[i, j]=\left{\begin{array}{ll}
c[i-1, j-1]+1 & \text { if } x[i]=y[j] \
\max (c[i, j-1], c[i-1, j]) & \text { otherwise }
\end{array}\right.$
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, m;
char a[N], b[N];
int f[N][N];
int main()
{
scanf("%d%d", &n, &m);
scanf("%s%s", a + 1, b + 1); // 从下标为1开始读
for (int i = 1; i <= n; i ++ )
{
for (int j = 1; j <= m; j ++ )
{
f[i][j] = max(f[i - 1][j], f[i][j - 1]);
if (a[i] == b[j]) f[i][j] = max(f[i][j], f[i - 1][j - 1] + 1);
}
}
printf("%d\n", f[n][m]);
return 0;
}2.4 最短编辑距离
给定两个字符串 A 和 B,现在要将 A 经过若干操作变为 B,可进行的操作有:
- 删除–将字符串 A 中的某个字符删除。
- 插入–在字符串 A 的某个位置插入某个字符。
- 替换–将字符串 A 中的某个字符替换为另一个字符。
求将 A 变为 B 至少需要进行多少次操作。
DP问题:
状态表示$f(i,j)$:
- 集合:所有将$a[1\sim i]$变成$b[1\sim j]$的操作方式
- 属性:$Min$
状态计算:
- 以对 $a$ 中的第 $i$ 个字母操作不同进行集合划分——$f(i,j)$
- 考虑最后一步操作,有三种操作方式,取最小值即可:
- 删(未删除前 $a$ 中前 $i-1$ 已经和 $b$ 的前 $j$ 个已经相同):$f(i-1,j)+1$
- 增(未添加前 $a$ 的前 $i$ 个已经和 $b$ 的前 $j-1$ 个已经相同):$f(i,j-1)+1$
- 改:$f(i-1,j-1)+1;or;0$
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, m;
char a[N], b[N];
int f[N][N];
int main()
{
scanf("%d%s", &n, a + 1);
scanf("%d%s", &m, b + 1);
// 初始化
for (int i = 0; i <= m; i ++ ) f[0][i] = i; // a中0个字母和b中i个字母匹配,增i次
for (int i = 0; i <= n; i ++ ) f[i][0] = i; // a中i个字母和b中0个字母匹配,删i次
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
{
f[i][j] = min(f[i - 1][j] + 1, f[i][j - 1] + 1);
if (a[i] == b[j])
f[i][j] = min(f[i][j], f[i - 1][j - 1]);
else
f[i][j] = min(f[i][j], f[i - 1][j - 1] + 1);
// 或直接写成f[i][j] = min(f[i][j], f[i - 1][j - 1] + (a[i] != b[j]));
}
printf("%d\n", f[n][m]);
return 0;
}三、区间DP
设有 $N$ 堆石子排成一排,其编号为 $1,2,3,…,N$。
每堆石子有一定的质量,可以用一个整数来描述,现在要将这 $N$ 堆石子合并成为一堆。
每次只能合并相邻的两堆,合并的代价为这两堆石子的质量之和,合并后与这两堆石子相邻的石子将和新堆相邻,合并时由于选择的顺序不同,合并的总代价也不相同。
例如有 4 堆石子分别为 1 3 5 2, 我们可以先合并 1、2 堆,代价为 4,得到 4 5 2, 又合并 1,2 堆,代价为 9,得到 9 2 ,再合并得到 11,总代价为 4+9+11=24;
如果第二步是先合并 2,3 堆,则代价为 7,得到 4 7,最后一次合并代价为 11,总代价为 4+7+11=22。
找出一种合理的方法,使总的代价最小,输出最小代价。
DP问题:
状态表示$f(i,j)$:
- 集合:所有将第 $i$ 堆石子到第 $j$ 堆石子合并成一堆石子的合并方式
- 属性:$Min$
状态计算:
集合划分——$f(i,j)$
以最后一次分界线的位置进行分类:
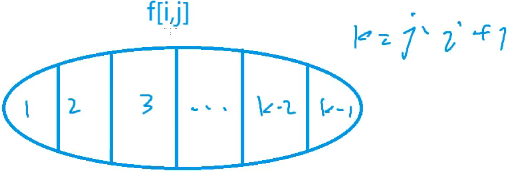
$k$为区间内的元素个数
状态转移方程示意图:

我们有:$f[i,j]=Min{f(i,k)+f(k+1,j)+s[j]-s[i-1]}$
求某一段的总和可以用前缀和来表示,即$s[j]-s[i-1]$
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 310;
int n;
int s[N];
int f[N][N];
int main()
{
scanf("%d", &n);
for (int i = 1; i <= n; i ++ ) scanf("%d", &s[i]);
for (int i = 1; i <= n; i ++ ) s[i] += s[i - 1];
for (int len = 2; len <= n; len ++ ) // len = 1,合并不需要代价
for (int i = 1; i + len - 1 <= n; i ++ )
{
int l = i, r = i + len - 1;
f[l][r] = 1e8;
for (int k = l; k < r; k ++ )
f[l][r] = min(f[l][r], f[l][k] + f[k + 1][r] + s[r] - s[l - 1]);
}
printf("%d\n", f[1][n]);
return 0;
}四、计数类DP
一个正整数 $n$ 可以表示成若干个正整数之和,形如:$n=n_1+n_2+…+n_k$,其中 $n_1≥n_2≥…≥n_k,k≥1$。
我们将这样的一种表示称为正整数 $n$ 的一种划分。
现在给定一个正整数 $n$,求出 $n$ 共有多少种不同的划分方法。
方法1:可看成完全背包问题:
DP问题:
状态表示$f(i,j)$:
- 集合
- $1∼i$中选体积(总和)恰好是$j$的选法的集合
- 属性:数量
- 集合
状态计算:
集合划分——$f(i,j)$
从$1-i$中选,总体积恰好等于$j$,并且选了两个$i$,与从$1∼i-1$中选,总体积等于$j-2i$
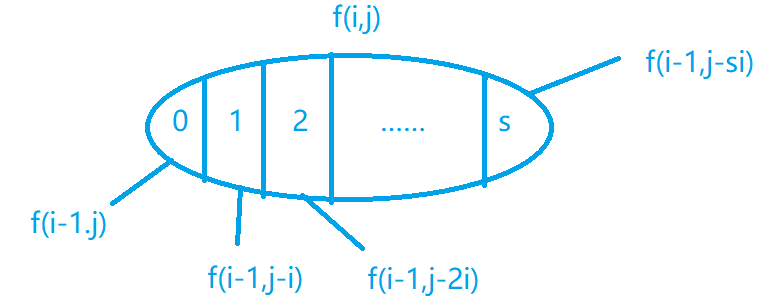
对完全背包问题优化(找规律):$f[i][j] = f[i - 1][j] + f[i][j - i]$
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010, mod = 1e9 + 7;
int n;
int f[N];
int main()
{
cin >> n;
f[0] = 1;
for (int i = 1; i <= n; i ++ )
for (int j = i; j <= n; j ++ )
f[j] = (f[j] + f[j - i]) % mod;
cout << f[n] << endl;
return 0;
}方法2:
DP问题:
状态表示$f(i,j)$:
- 集合
- 所有总和为$i$,并且恰好可以表示成$j$个数的和的方案
- 属性:数量
- 集合
状态计算:
集合划分——$f(i,j)$
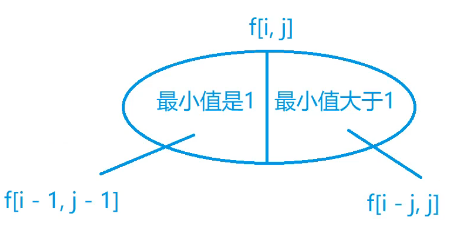
- 最大值大于1,则将每个数减去1,可将其任何一种方案变成和是$i-j$,分成$j$个数的方案
$f[i,j]=f[i-1,j-1]+f[i-j,j]$
$ans=f[n,1]+f[n,2]+…+f[n,n]$
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010, mod = 1e9 + 7;
int n;
int f[N][N];
int main()
{
cin >> n;
f[1][1] = 1;
for (int i = 2; i <= n; i ++ )
for (int j = 1; j <= i; j ++ )
f[i][j] = (f[i - 1][j - 1] + f[i - j][j]) % mod;
int res = 0;
for (int i = 1; i <= n; i ++ ) res = (res + f[n][i]) % mod;
cout << res << endl;
return 0;
}五、数位统计DP
给定两个整数 $a$ 和 $b$,求 $a$ 和 $b$ 之间的所有数字中 0∼9 的出现次数。
例如,$a=1024$,$b=1032$,则 $a$ 和 $b$ 之间共有 9 个数如下:
1024 1025 1026 1027 1028 1029 1030 1031 1032其中 0 出现 10 次,1 出现 10 次,2 出现 7 次,3 出现 3 次等等…
前缀思想:区间答案—-转化为—->前缀答案
$count(n,x)$为 $1\sim n$ 中 $x$ 出现的次数,则答案为$count(b,x)-count(a-1,x)$
$1\sim n$,$x=1$,$n=abcdefg$,分别求出$1$在每一位上出现的次数。
如求$1$在第$4$位上出现的次数,则在$1\leq xxx1yyy\leq abcdefg$
$xxx=000\sim abc-1$,$yyy=000\sim 999$,共有$abc*1000$种情况
注意:当求$0$在某位的出现次数时,由于前导零的存在,$xxx$应从$001$开始枚举
$xxx=abc$
- $d<1$,$abc1yyy>abc0efg$,方案数为$0$
- $d=1$,$yyy=000\sim efg$,方案数为$efg+1$
- $d>1$,$yyy=000\sim 999$,方案数为$1000$
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 10;
/*
001~abc-1, 999
abc
1. num[i] < x, 0
2. num[i] == x, 0~efg
3. num[i] > x, 0~999
*/
int get(vector<int> num, int l, int r) // 求特定区间的位组成的数字是多少
{
int res = 0;
for (int i = l; i >= r; i -- ) res = res * 10 + num[i];
return res;
}
int power10(int x) // 求10的i次方
{
int res = 1;
while (x -- ) res *= 10;
return res;
}
int count(int n, int x)
{
if (!n) return 0;
vector<int> num;
while (n)
{
num.push_back(n % 10); // 抠出n的每一位
n /= 10;
}
n = num.size();
int res = 0;
for (int i = n - 1 - !x; i >= 0; i -- ) // 当x = 0时,不需要枚举最高位
{
if (i < n - 1)
{
res += get(num, n - 1, i + 1) * power10(i);
if (!x) res -= power10(i); // x = 0时,组成的数字从1开始枚举
}
if (num[i] == x) res += get(num, i - 1, 0) + 1;
else if (num[i] > x) res += power10(i);
}
return res;
}
int main()
{
int a, b;
while (cin >> a >> b , a)
{
if (a > b) swap(a, b);
for (int i = 0; i <= 9; i ++ )
cout << count(b, i) - count(a - 1, i) << ' ';
cout << endl;
}
return 0;
}六、状态压缩DP
思想:用一个整数(二进制数)表示某个状态($n$一般较小)
求把 $N×M$ 的棋盘分割成若干个 $1×2$ 的长方形,有多少种方案。
DP问题:
状态表示$f(i,j)$:
集合:所有摆到了第$i$列,上一列伸出来小方格的状态是$j$的情况下的方案数(如下所示$j=(10010)_2$)
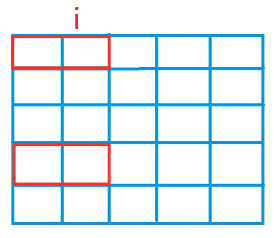
属性:数量
状态计算:
集合划分——$f(i,j)$
如下图,$j=01001,k=10010$
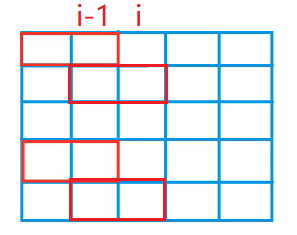
需满足:
$(j&k)==0$—>不存在冲突
$j|k$不存在连续奇数个$0$
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 12, M = 1 << N;
int n, m;
long long f[N][M];
bool st[M];
int main()
{
while (cin >> n >> m, n || m)
{
// 是否存在连续奇数个0
for (int i = 0; i < 1 << n; i ++ )
{
int cnt = 0; // 当前段连续0的个数
st[i] = true;
for (int j = 0; j < n; j ++ )
if (i >> j & 1) // 上一段已经截止
{
if (cnt & 1) st[i] = false; // 上一段是奇数个0,不合法
cnt = 0;
}
else cnt ++ ;
if (cnt & 1) st[i] = false; // 最后一段0的个数
}
memset(f, 0, sizeof f);
f[0][0] = 1; // 第1列是0时,有一种方案
for (int i = 1; i <= m; i ++ ) // 枚举i列
for (int j = 0; j < 1 << n; j ++ )
for (int k = 0; k < 1 << n; k ++ )
if ((j & k) == 0 && st[j | k])
f[i][j] += f[i - 1][k];
cout << f[m][0] << endl; // 第m列没有伸出来的方块才是合法的答案
}
return 0;
}给定一张 $n$ 个点的带权无向图,点从 $0∼n−1$ 标号,求起点 $0$ 到终点 $n−1$ 的最短 Hamilton 路径。
Hamilton 路径的定义是从 $0$ 到 $n−1$ 不重不漏地经过每个点恰好一次。
DP问题:
状态表示$f(i,j)$:
- 集合
- 所有从$0$走到$j$,**走过的所有点是$i$**的所有路径($i$是二进制数,每一位分别表示当前点是否走过)
- 属性:$Min$
- 集合
状态计算:
集合划分——$f(i,j)$
以倒数第二个点是哪个点进行分类:
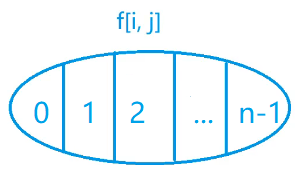
0—>k—>j:$f(i,j)=min(f(i-{j},k)+a[k,j])$
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 20, M = 1 << N;
int n;
int w[N][N]; // 边的权值
int f[M][N]; // 状态
int main()
{
cin >> n;
for (int i = 0; i < n; i ++ )
for (int j = 0; j < n; j ++ )
cin >> w[i][j];
memset(f, 0x3f, sizeof f); // 初始化为正无穷
f[1][0] = 0;
for (int i = 0; i < 1 << n; i ++ )
for (int j = 0; j < n; j ++ )
if (i >> j & 1) // 从0走到j,i中包含j
for (int k = 0; k < n; k ++ )
if (i >> k & 1)
f[i][j] = min(f[i][j], f[i - (1 << j)][k] + w[k][j]);
cout << f[(1 << n) - 1][n - 1];
return 0;
}七、树形DP
6.1 例1:树的最长路径
给定一棵树,树中包含 $n$ 个结点(编号 $1-n$)和 $n−1$ 条无向边,每条边都有一个权值。
现在请你找到树中的一条最长路径。
换句话说,要找到一条路径,使得使得路径两端的点的距离最远。
注意:路径中可以只包含一个点。
输入格式
第一行包含整数 $n$。
接下来 $n−1$ 行,每行包含三个整数 $a_i,b_i,c_i$,表示点 $a_i$ 和 $b_i$ 之间存在一条权值为 $c_i$ 的边。
输出格式
输出一个整数,表示树的最长路径的长度。
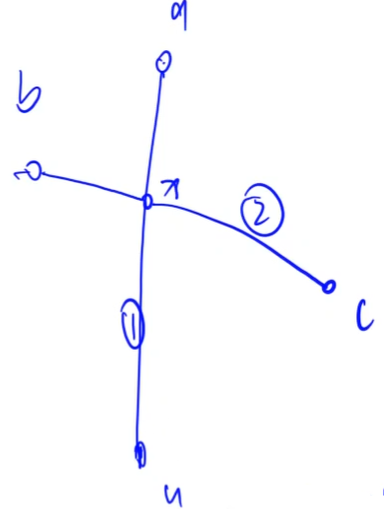
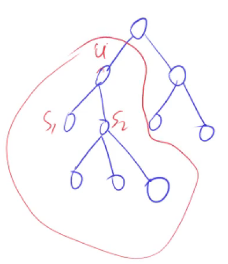
我们将树按照某个点为根进行展开得到以下树,所有路径经过的最高的点为 $u$:
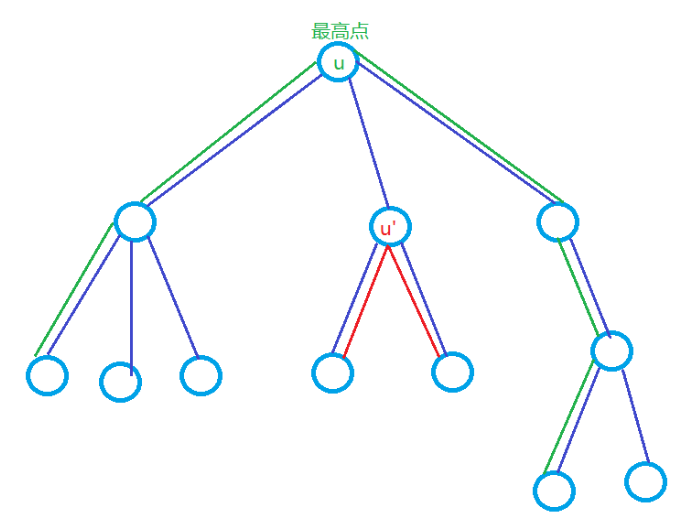
DP问题:
状态表示$f(0/1,j)$:
- 集合
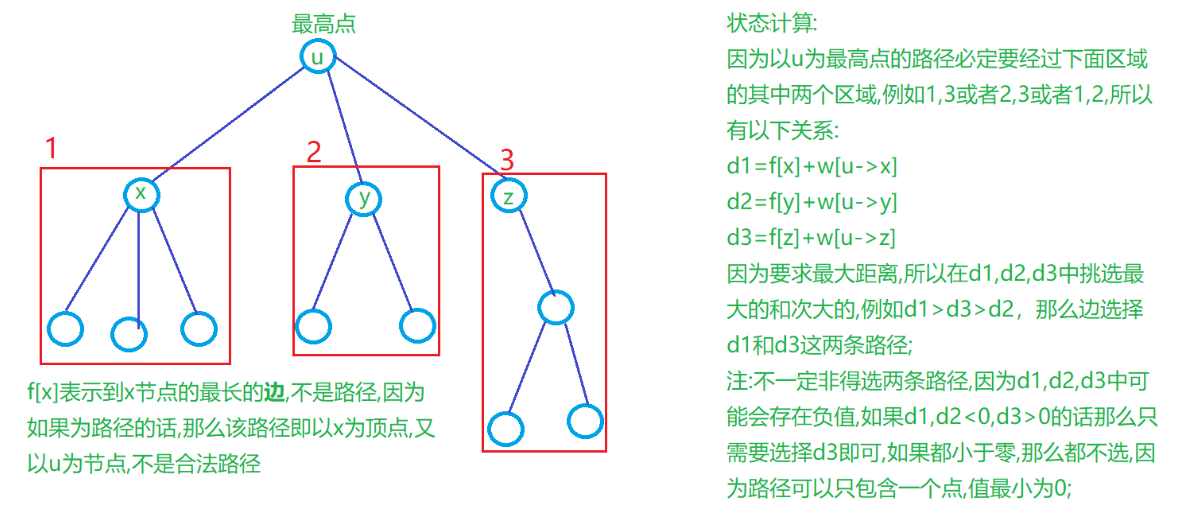
- 以节点 $i$ 为根的子树中,从子树某一个节点到 $i$ 的最长路为 $f(0,i)$,次长路为 $f(1,i)$
- 属性:$Max$
- 集合
状态计算:
如果子节点的最长路加上对应边后大于当前的最长路,那么就更新最长路
否则如果大于次长路,那么就更新次长路
状态转移方程:
$\left{\begin{array}{c}
f_{0, i}=\max \limits_{s \in \text { son }{i}}\left{f{0, s}+w_{i, s}\right} \
f_{1, i}=\max \limits_{s \in \text { soni } \text { and } f_{0, s}+w_{i, s}<f_{0, i}}\left{f_{0, s}+w_{i, s}\right}
\end{array}\right.$
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 10010, M = N * 2; // 无向边边数*2
int n;
int h[N], e[M], w[M], ne[M], idx;
int ans;
void add(int a, int b, int c)
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
int dfs(int u, int father)
{
int dist = 0; // 表示从当前点往下走的最大长度
int d1 = 0, d2 = 0;
for (int i = h[u]; i != -1; i = ne[i]) // ~i 等同于 i!=-1
{
int j = e[i];
// father保证DFS不往回走, 避免造成死循环
if (j == father) continue;
int d = dfs(j, u) + w[i]; // w[i] 为当前点与子节点边的权值
dist = max(dist, d);
if (d >= d1) d2 = d1, d1 = d;
else if (d > d2) d2 = d;
}
ans = max(ans, d1 + d2);
return dist;
}
int main()
{
cin >> n;
memset(h, -1, sizeof h);
for (int i = 0; i < n - 1; i ++ )
{
int a, b, c;
cin >> a >> b >> c;
add(a, b, c), add(b, a, c);
}
dfs(1, -1);
cout << ans << endl;
return 0;
}无边权的树的最长路径(直径)可以由以下算法得到:
- 任取一点作为起点,找到距离该点最远的一个点 $u$,可用 BFS
- 再找到距离 $u$ 最远的一点 $v$,可用 BFS
那么 $u$ 和 $v$ 之间的路径就是一条直径。
证明
假设 $a$ 和 $u$ 是由第一步得到的直径,$b$ 和 $c$ 是一条真正的直径。
case 1:两条直径不相交
由于 $u$ 是距离 $a$ 最远的点,则有 边 $1\geq$ 边 $2+$ 边 $3$,则有边 $1+$ 边 $2\geq$ 边 $3$
则 $b$ 到 $u$ 的距离大于等于 $b$ 到 $c$ 的距离,则 $u$ 必然是某个直径的端点
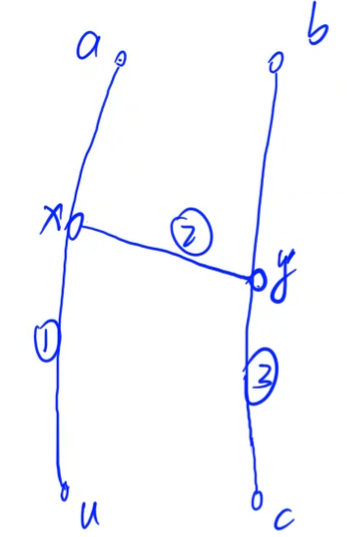
case 2:两条直径存在交点
由于 $u$ 是距离 $a$ 最远的点,则有 边 $1\geq$ 边 $2$,则 $b$ 到 $u$ 的距离大于等于 $b$ 到 $c$ 的距离,则 $u$ 必然是某个直径的端点
6.2 例2:没有上司的舞会
Ural 大学有 $N$ 名职员,编号为 $1∼N$。
他们的关系就像一棵以校长为根的树,父节点就是子节点的直接上司。
每个职员有一个快乐指数,用整数 $H_i$ 给出,其中 $1≤i≤N$。
现在要召开一场周年庆宴会,不过,没有职员愿意和直接上司一起参会。
在满足这个条件的前提下,主办方希望邀请一部分职员参会,使得所有参会职员的快乐指数总和最大,求这个最大值。
DP问题:
状态表示$f(u,0; or ; 1)$:
集合
$f(u,0)$表示所有从以 $u$ 为根的子树中选择,并且不选 $u$ 这个点的方案
$f(u,1)$表示所有从以 $u$ 为根的子树中选择,并且选 $u$ 这个点的方案
属性:$Max$
状态计算:
- $f(u,0)=\sum_i max(f(s_i,0),f(s_i,1))$
- $f(u,1)=\sum_i f(s_i,0)$(选了上司,直接职员则不选择)
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 6010;
int n;
int h[N], e[N], ne[N], idx;
int happy[N];
int f[N][2];
bool has_fa[N]; // 存储点是否有父节点
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
void dfs(int u)
{
f[u][1] = happy[u];
for (int i = h[u]; ~i; i = ne[i]) // ~i即i按位取反是否为0,也即i!=-1
{
int j = e[i];
dfs(j);
f[u][1] += f[j][0];
f[u][0] += max(f[j][0], f[j][1]);
}
}
int main()
{
scanf("%d", &n);
for (int i = 1; i <= n; i ++ ) scanf("%d", &happy[i]);
memset(h, -1, sizeof h);
for (int i = 0; i < n - 1; i ++ )
{
int a, b;
scanf("%d%d", &a, &b);
add(b, a); // b是a的父节点,在邻接表中插入一条边b->a
has_fa[a] = true;
}
int root = 1;
while (has_fa[root]) root ++ ;
dfs(root);
printf("%d\n", max(f[root][0], f[root][1]));
return 0;
}6.3 例3:皇宫看守
太平王世子事件后,陆小凤成了皇上特聘的御前一品侍卫。
皇宫各个宫殿的分布,呈一棵树的形状,宫殿可视为树中结点,两个宫殿之间如果存在道路直接相连,则该道路视为树中的一条边。
已知,在一个宫殿镇守的守卫不仅能够观察到本宫殿的状况,还能观察到与该宫殿直接存在道路相连的其他宫殿的状况。
大内保卫森严,三步一岗,五步一哨,每个宫殿都要有人全天候看守,在不同的宫殿安排看守所需的费用不同。
可是陆小凤手上的经费不足,无论如何也没法在每个宫殿都安置留守侍卫。
帮助陆小凤布置侍卫,在看守全部宫殿的前提下,使得花费的经费最少。
输入格式
输入中数据描述一棵树,描述如下:
第一行 $n$,表示树中结点的数目。
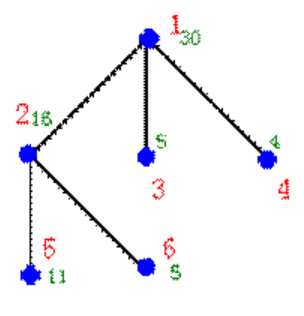
第二行至第 $n+1$ 行,每行描述每个宫殿结点信息,依次为:该宫殿结点标号 $i$,在该宫殿安置侍卫所需的经费 $k$,该结点的子结点数 $m$,接下来 $m$ 个数,分别是这个结点的 $m$ 个子结点的标号 $r_1,r_2,…,r_m$。
对于一个 $n$ 个结点的树,结点标号在 $1$ 到 $n$ 之间,且标号不重复。
输出格式
输出一个整数,表示最少的经费。
本题要求图中每个点都被观察到:
- 父节点 放置 哨兵,所有子节点都 可放可不放 哨兵
- 父节点 不放 哨兵,但是他至少有一个 子节点 放置哨兵,观察住了他
- 父节点 不放 哨兵,但 父节点 的 父节点 放置哨兵观察,则 子节点 可放可不放 哨兵
则每个节点有以下三种情况:
- 被父节点观察 (0)
- 被子节点观察 (1)
- 被自己来观察 (2)
状态表示:$f_{i,0/1/2}$
- 集合: 以结点 $i$ 为 根节点 的子树,在 $i$ 状态为 $j$ 的方案
- 属性:方案中,放置哨兵的代价最少【最小花费】
状态计算:
- 在 $i$ 上被父节点观察 (0):
$f_{i, 0} =\sum_{i_{c h}} \min \left(f_{i_{c h}, 1}, f_{i_{c h}, 2}\right)$,其中 $i_{c h} \in{\text { ver } \mid \text { ver } \text { 是 } \mathrm{i} \text { 的子节点 }}$
- 在 $i$ 上被子节点观察 (1) :
$f_{i, 1}=\min \left(f_{i_{c h}, 2}+\sum_{\text {other } i_{c h}} \min \left(f_{ {\text {other } {i_{c h}, 1}}}, f_{\text {other } i_{c h}, 2}\right)\right)$,其中 $i_{c h} \in{v e r \mid v e r \text { 是 } \mathrm{i} \text { 的子节点 }} \quad \text { other } i_{c h} \in\left{v e r \mid v e r \text { 是 } \mathrm{i} \text { 的子节点, 且 } v e r \neq i_{c h}\right}$
- 在 $i$ 上被自己来观察 (2) :
$f_{i, 2}=\sum_{i_{c h}} \min \left{f_{i_{c h}, 0}, f_{i_{c h}, 1}, f_{i_{c h}, 2}\right}+w_{i}$,其中 $i_{c h} \in{v e r \mid v e r \text { 是 } \mathrm{i} \text { 的子节点 }}$
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1510;
int n;
int h[N], w[N], e[N], ne[N], idx;
int f[N][3];
bool st[N];
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
void dfs(int u)
{
f[u][2] = w[u];
for (int i = h[u]; ~i; i = ne[i])
{
int j = e[i]; // 遍历所有子节点
dfs(j);
f[u][0] += min(f[j][1], f[j][2]);
f[u][2] += min(min(f[j][0], f[j][1]), f[j][2]);
}
f[u][1] = 1e9;
for (int i = h[u]; ~i; i = ne[i])
{
int j = e[i];
// f[u][0]为所有子节点的摆放方案代价之和, 减去 min(f[j][1], f[j][2]) 即是除了j节点其余节点的代价之和
f[u][1] = min(f[u][1], f[j][2] + f[u][0]- min(f[j][1], f[j][2]));
}
}
int main()
{
cin >> n;
memset(h, -1, sizeof h);
for (int i = 1; i <= n; i ++ )
{
int id, cost, cnt;
cin >> id >> cost >> cnt;
w[id] = cost; // 点上记录花费
while (cnt -- )
{
int ver;
cin >> ver;
add(id, ver);
st[ver] = true; // 标记不是根节点
}
}
int root = 1;
while (st[root]) root ++ ; // 找到根节点
dfs(root);
cout << min(f[root][1], f[root][2]) << endl;
return 0;
}八、记忆化搜索(备忘录法)
递归实现方式
给定一个 $R$ 行 $C$ 列的矩阵,表示一个矩形网格滑雪场。
矩阵中第 $i$ 行第 $j$ 列的点表示滑雪场的第 $i$ 行第 $j$ 列区域的高度。
一个人从滑雪场中的某个区域内出发,每次可以向上下左右任意一个方向滑动一个单位距离。
当然,一个人能够滑动到某相邻区域的前提是该区域的高度低于自己目前所在区域的高度。
现在给定你一个二维矩阵表示滑雪场各区域的高度,请你找出在该滑雪场中能够完成的最长滑雪轨迹,并输出其长度(可经过最大区域数)。
DP问题:
状态表示$f(i,j)$:
- 集合
- 所有从$(i,j)$开始滑的路径
- 属性:$Max$
- 集合
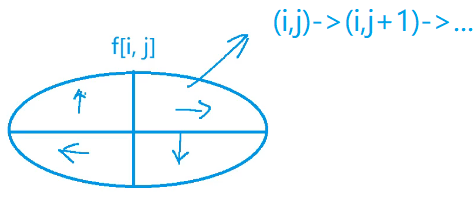
状态计算:
按第一步往哪个方向滑
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 310;
int n, m;
int g[N][N];
int f[N][N];
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
int dp(int x, int y)
{
int &v = f[x][y]; // 引用符号,C++特性
if (v != -1) return v;
v = 1;
for (int i = 0; i < 4; i ++ )
{
int a = x + dx[i], b = y + dy[i]; // 上下左右四个方向
if (a >= 1 && a <= n && b >= 1 && b <= m && g[x][y] > g[a][b])
v = max(v, dp(a, b) + 1);
}
return v;
}
int main()
{
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
scanf("%d", &g[i][j]);
memset(f, -1, sizeof f);
int res = 0;
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
res = max(res, dp(i, j));
printf("%d\n", res);
return 0;
}