算法程序设计

算法学习

发布日期: 2022-09-21

更新日期: 2022-12-15

文章字数: 4.6k

阅读时长: 25 分

第0次

第4题有趣的数

有趣的数满足以下三个条件：

它的数字只包含 0,1,2,3，且这四个数字都出现过至少一次。
所有的 0 都出现在所有的 1 之前，而所有的 2 都出现在所有的 3 之前。
最高位数字不为 0。

本题为组合计数问题，对应算法笔记第四章(数学知识)。

将0、1分为一组，将2、3分为一组，在0、1中选k位，在2、3中选n-k位，而由于最高位数字不能为0，而所有0都在所有1之前，所以最高位没有0或1，则在剩下的n-1位中选k位，对应组合数$C_{n-1}^k$。0的个数有k-1种可能，2的个数有n-k-1种可能，则答案为：$\sum_{k=2}^{n-2}C_{n-1}^{k}(k-1)(n-k-1)$。

//组合计数问题
#include<iostream>
using namespace std;

typedef long long ll;
const int N = 1010,MOD = 1e9 + 7;
int n;
int c[N][N];


int main()
{
    scanf("%d",&n);
    //求所有数的组合数
    for(int i = 0; i <= n; i++)
    {
        for(int j = 0; j <= i; j++)
        {
            if(!j) c[i][j] = 1;
            else
            {
                c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % MOD;
            }
        }
    }
    //计算公式为sum(c[n-1][k]*(k-1)*(n-k-1))(k从2到n-2)
    int res = 0;
    for(int k = 2; k <= n - 2; k++)
    {
        res = (res + (ll)c[n-1][k]*(k-1)*(n-k-1)) % MOD;
    }
    printf("%d",res);
    return 0;
}

第1次

第3题命令行选项

stringstream定义于头文件<sstream>中，掌握其构造方式和分割字符串的方法
- stringstream ssin(str); // stringstream读入字符串
- while (ssin >> str) ops.push_back(str); // stringstream以空格的方式分割字符串
运用vector存储答案

#include <iostream>
#include <cstring>
#include <sstream>
#include <algorithm>

using namespace std;

const int N = 30;

int n;
bool o1[N], o2[N];
string ans[N];

int main()
{
    string str;
    cin >> str;
    for (int i = 0; i < str.size(); i ++ )
        if (i + 1 < str.size() && str[i + 1] == ':')
        {
            o2[str[i] - 'a'] = true;
            i ++ ;
        }
        else o1[str[i] - 'a'] = true;

    cin >> n;
    getchar();  					// 将n后面的回车过滤掉
    for (int C = 1; C <= n; C ++ )
    {
        printf("Case %d:", C);
        getline(cin, str);			// 将整行字符读入,包括空格
        stringstream ssin(str);		// stringstream读入字符串
        vector<string> ops;
        while (ssin >> str) ops.push_back(str);		// stringstream以空格的方式分割字符串
        for (int i = 0; i < 26; i ++ ) ans[i].clear();
        for (int i = 1; i < ops.size(); i ++ )
        {
            if (ops[i][0] != '-' || ops[i][1] < 'a' || ops[i].size() != 2) break;
            int k = ops[i][1] - 'a';
            if (o1[k]) ans[k] = "*";
            else if (o2[k] && i + 1 < ops.size()) ans[k] = ops[i + 1], i ++ ;
            else break;
        }
        for (int i = 0; i < 26; i ++ )
            if (ans[i].size())
            {
                cout << " -" << (char)(i + 'a');
                if (o2[i]) cout << ' ' << ans[i];
            }
        cout << endl;
    }
    return 0;
}

第3次

第3题集合竞价

我的代码：

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;

const int N = 5010;
typedef long long ll;
struct record
{
    char action;
    double p;
    ll s;
    bool is_del;
}record[N];

int main()
{
    string str;
    ll n = 0, s, res = 0;
    double p, rp = 0;
    while(cin >> str)
    {
        switch(str[0])
        {
            case 'b':
            case 's':
                scanf("%lf",&p);
                scanf("%lld",&s);
                record[++n] = {str[0], p, s, true};
                break;
            case 'c':
                scanf("%lld",&s);
                record[++n].is_del = false;
                record[s].is_del = false;
        }
    }
    for(int i = 1; i <= n; i++)
    {
        if(record[i].is_del)
        {
            ll k1 = 0, k2 = 0;
            
            for(int j = 1; j <= n; j++)
            {
                if(record[j].is_del)
                {
                    if(record[j].action == 'b' && record[j].p >= record[i].p)
                    {
                        k1 += record[j].s;
                    }
                    if(record[j].action == 's' && record[j].p <= record[i].p)
                    {
                        k2 += record[j].s;
                    }
                }
            }
            
            if((res == min(k1,k2) && rp < record[i].p) || res < min(k1,k2))
            {
                res = min(k1,k2);
                rp = record[i].p;
            }
        }
    }
    
    printf("%.2lf %lld",rp,res);
    
    return 0;
}

前缀和+双指针$O(nlogn)$：

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

typedef long long LL;
const int N = 5010;

int n;
struct Data
{
    int type;
    double p;
    int c;
    bool st;
    bool operator< (const Data& t) const
    {
        return p < t.p;
    }
}d[N], buy[N], sell[N];
LL s1[N], s2[N];
double ps[N];

int main()
{
    string op;
    while (cin >> op)
    {
        ++ n;
        double p;
        int c;
        if (op == "cancel")
        {
            cin >> c;
            d[c].st = true;
            d[n].st = true;
        }
        else if (op == "buy")
        {
            cin >> p >> c;
            d[n] = {1, p, c};
        }
        else
        {
            cin >> p >> c;
            d[n] = {2, p, c};
        }
    }

    int k1 = 0, k2 = 0;
    int cnt = 0;
    for (int i = 1; i <= n; i ++ )
    {
        if (d[i].st) continue;
        ps[cnt ++ ] = d[i].p;
        if (d[i].type == 1) buy[ ++ k1] = d[i];
        else sell[ ++ k2] = d[i];
    }

    sort(buy + 1, buy + k1 + 1);
    sort(sell + 1, sell + k2 + 1);

    for (int i = 1; i <= k1; i ++ )
        s1[i] = s1[i - 1] + buy[i].c;
    for (int i = 1; i <= k2; i ++ )
        s2[i] = s2[i - 1] + sell[i].c;

    sort(ps, ps + cnt);
    double resp;
    LL resc = -1;
    for (int k = cnt - 1, i = k1, j = k2; k >= 0; k -- )
    {
        double p = ps[k];
        while (buy[i - 1].p >= p) i -- ;
        while (sell[j - 1].p > p) j -- ;
        if (sell[j].p > p) j -- ;
        if (buy[i].p >= p)
        {
            LL t = min(s1[k1] - s1[i - 1], s2[j]);
            if (t > resc) resp = p, resc = t;
        }
    }

    printf("%.2lf %lld\n", resp, resc);
    return 0;
}

第4次

第3题节日

y总的代码：

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

int months[13] = {
    0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31
};		// 按每个月的天数开一个数组

int is_leap(int year)
{
    if (year % 4 == 0 && year % 100 || year % 400 == 0)
        return 1;
    return 0;
}

int get_days(int year, int month)  // 求某月有多少天
{
    if (month == 2) return months[month] + is_leap(year);
    return months[month];
}

int main()
{
    int a, b, c, y1, y2;
    cin >> a >> b >> c >> y1 >> y2;
    int days = 0;
    for (int year = 1850; year <= y2; year ++ )
        for (int month = 1; month <= 12; month ++ )
        {
            if (year >= y1 && month == a)
            {
                int w = (1 + days) % 7, cnt = 0;		// 星期以0开始
                for (int d = 1; d <= get_days(year, month); d ++ )
                {
                    if (w == c - 1)	
                    {
                        cnt ++ ;		// 星期c的个数++
                        if (cnt == b)
                        {
                            printf("%04d/%02d/%02d\n", year, month, d);
                            break;
                        }
                    }
                    w = (w + 1) % 7;
                }
                if (cnt < b) puts("none");
            }
            days += get_days(year, month);		// 加上这个月的天数
        }

    return 0;
}

我的代码：

#include<iostream>
using namespace std;

int e[210][375];
int day[210];           // 存储一年有多少天
int month[20];          // 存储一月有多少天,采用累计形式

int main()
{
    int a, b, c, y1, y2;        // a月b星期c日期
    scanf("%d%d%d%d%d", &a, &b, &c, &y1, &y2);
    // 预处理
    int week = 2;
    for(int i = 0; i <= 200; i++)
    {
        int year = 1850 + i;
        if((year % 400 == 0) || (year % 4 == 0 && year % 100 != 0))
            day[i] = 366;
        else
            day[i] = 365;
        for(int j = 1; j <= day[i]; j++)
        {
            e[i][j] = week++;
            if(week > 7)
                week %= 7;
        }
    }
    
    // 预处理每个月天数的前缀和
    month[1] = 0;
    for(int i = 2; i <= a + 1; i++)
    {
        if(i == 2 || i == 4 || i == 6 || i == 8 || i == 9 || i == 11)   // 看成前面一月
            month[i] += month[i - 1] + 31;
        else if(i == 3)
            month[i] += month[i - 1] + 28;
        else
            month[i] += month[i - 1] + 30;
    }

    // 对每年求解
    for(int i = y1 - 1850; i <= y2 - 1850; i++)
    {
        int month_day = month[a] + 1, count = 0;
        
        if(day[i] == 366 && a >= 3)         // 闰年需+1
            month_day += 1;
            
        while(count != b)
        {
            if(e[i][month_day] == c)
                count++;
            month_day++;
        }
        
        month_day -= 1;     // 多加了个1
        
        // 判断该值是否存在
        if(month_day > month[a + 1] 
            && !(day[i] == 366 && month_day == month[a + 1] + 1))                   // 不是闰年
        {
            printf("none\n");
            continue;
        }
        
        if(day[i] == 366 && a >= 3)
            printf("%d/%02d/%02d\n", i + 1850, a, month_day - month[a] - 1);        // month[a]算的是非闰年的
        else
            printf("%d/%02d/%02d\n", i + 1850, a, month_day - month[a]);
    }
    
    return 0;
}

第16次

第2题二十四点)

#include <iostream>
#include <cstring>
#include <algorithm>
#include <stack>
#include <unordered_map>

using namespace std;

stack<int> num;
stack<char> op;

void eval()
{
    int b = num.top(); num.pop();
    int a = num.top(); num.pop();
    char c = op.top(); op.pop();
    int x;
    if (c == '+') x = a + b;
    else if (c == '-') x = a - b;
    else if (c == 'x') x = a * b;
    else
    {
        if (a * b >= 0) x = a / b;
        else  // 向下取整。C++中a/b是向零取整
        {
            if (a % b == 0) x = a / b;
            else x = a / b - 1;
        }
    }
    num.push(x);
}

int main()
{
    unordered_map<char, int> pr;
    pr['+'] = pr['-'] = 1;
    pr['x'] = pr['/'] = 2;
    int n;
    cin >> n;
    while (n -- )
    {
        string str;
        cin >> str;
        num = stack<int>();
        op = stack<char>();
        for (auto c: str)
            if (c >= '0' && c <= '9') num.push(c - '0');
            else
            {
                while (op.size() && pr[op.top()] >= pr[c]) eval();
                op.push(c);
            }
        while (op.size()) eval();
        if (num.top() == 24) puts("Yes");
        else puts("No");
    }
    return 0;
}

第18次

第3题化学方程式

#include <iostream>
#include <cstring>
#include <algorithm>
#include <unordered_map>

#define x first
#define y second

using namespace std;

typedef unordered_map<string, int> MPSI;		// 基于哈希表

MPSI dfs(string& str, int& u)
{
    MPSI res;
    while (u < str.size())
    {
        if (str[u] == '(')
        {
            u ++ ;  // 过滤掉 '('
            auto t = dfs(str, u);
            u ++ ;  // 过滤掉 ')'
            int cnt = 1, k = u;
            while (k < str.size() && isdigit(str[k])) k ++ ;	// 看括号后是否有数字
            if (k > u)
            {
                cnt = stoi(str.substr(u, k - u));
                u = k;
            }
            for (auto c: t)
                res[c.x] += c.y * cnt;
        }
        else if (str[u] == ')') break;		// 返回上一层
        else
        {
            int k = u + 1;				   // 将字母完整找出
            while (k < str.size() && str[k] >= 'a' && str[k] <= 'z') k ++ ;
            auto key = str.substr(u, k - u);
            u = k;
            int cnt = 1;
            while (k < str.size() && isdigit(str[k])) k ++ ;
            if (k > u)			// 有数字
            {
                cnt = stoi(str.substr(u, k - u));
                u = k;
            }
            res[key] += cnt;
        }
    }
    return res;
}

MPSI work(string str)
{
    MPSI res;
    for (int i = 0; i < str.size(); i ++ )
    {
        int j = i + 1;
        while (j < str.size() && str[j] != '+') j ++ ;
        auto item = str.substr(i, j - i);
        i = j;
        int cnt = 1, k = 0;
        while (k < item.size() && isdigit(item[k])) k ++ ;		// isdigit是库函数, 判断是否为数字
        if (k) cnt = stoi(item.substr(0, k));	// 处理系数, string to int, 将字符串转换为数字
        auto t = dfs(item, k);
        for (auto c: t)
            res[c.x] += c.y * cnt;
    }
    return res;
}

int main()
{
    int n;
    cin >> n;
    while (n -- )
    {
        string str;
        cin >> str;
        int k = str.find('=');
        auto left = work(str.substr(0, k)), right = work(str.substr(k + 1));
        if (left == right) puts("Y");
        else puts("N");
    }
    return 0;
}

第21次

第2题期末预测之最佳阈值

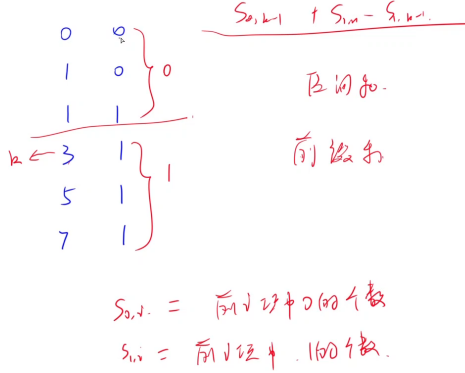
$S_{0,i}=前i项中0的个数$
$S_{1,i}=前i项中1的个数$
$预测结果=S_{0,k-1}+S_{1,n}-S_{1,k-1}$

#include <iostream>
#include <cstring>
#include <algorithm>

#define x first
#define y second

using namespace std;

typedef pair<int, int> PII;
const int N = 100010;

int n;
PII q[N];
int s[2][N];

int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; i ++ ) scanf("%d%d", &q[i].x, &q[i].y);
    sort(q + 1, q + n + 1);
    for (int i = 0; i < 2; i ++ )
        for (int j = 1; j <= n; j ++ )
            s[i][j] = s[i][j - 1] + (q[j].y == i);

    int cnt = -1, res;
    for (int i = 1; i <= n; i ++ )
    {
        int t = s[0][i - 1] + s[1][n] - s[1][i - 1];
        if (t >= cnt) cnt = t, res = q[i].x;
        while (i + 1 <= n && q[i + 1].x == q[i].x) i ++ ;	// 分界线两侧的数必须不同
    }
    printf("%d\n", res);
    return 0;
}

第22次

第2题邻域均值

求子矩阵的和使用二维前缀和

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 610;

int n, L, r, t;
int s[N][N];

int get_sum(int x1, int y1, int x2, int y2)
{
    return s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1];
}

int get_cnt(int x1, int y1, int x2, int y2)
{
    return (x2 - x1 + 1) * (y2 - y1 + 1);
}

int main()
{
    scanf("%d%d%d%d", &n, &L, &r, &t);
    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= n; j ++ )
        {
            int x;
            scanf("%d", &x);
            s[i][j] = x + s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];
        }

    int res = 0;
    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= n; j ++ )
        {
            int x1 = max(1, i - r), y1 = max(1, j - r);
            int x2 = min(n, i + r), y2 = min(n, j + r);
            if (get_sum(x1, y1, x2, y2) <= t * get_cnt(x1, y1, x2, y2))
                res ++ ;
        }
    printf("%d\n", res);
    return 0;
}

第3题 DHCP服务器

模拟题
每个IP维护三个变量，即状态、过期时间、占用者

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 10010;

int n, m, t_def, t_max, t_min;
string h;
struct IP
{
    int state;   // 0：未分配，1：待分配，2：占用，3：过期
    int t;  	 // 过期时间
    string owner;
}ip[N];

void update_ips_state(int tc)
{
    for (int i = 1; i <= n; i ++ )
        if (ip[i].t && ip[i].t <= tc)
        {
            if (ip[i].state == 1)
            {
                ip[i].state = 0;
                ip[i].owner = "";
                ip[i].t = 0;
            }
            else
            {
                ip[i].state = 3;
                ip[i].t = 0;
            }
        }
}

int get_ip_by_owner(string client)
{
    for (int i = 1; i <= n; i ++ )
        if (ip[i].owner == client)
            return i;
    return 0;
}

int get_ip_by_state(int state)
{
    for (int i = 1; i <= n; i ++ )
        if (ip[i].state == state)
            return i;
    return 0;
}

int main()
{
    cin >> n >> t_def >> t_max >> t_min >> h;
    cin >> m;

    while (m -- )
    {
        int tc;
        string client, server, type;
        int id, te;
        cin >> tc >> client >> server >> type >> id >> te;
        if (server != h && server != "*")
        {
            if (type != "REQ") continue;
        }
        if (type != "DIS" && type != "REQ") continue;
        if (server == "*" && type != "DIS" || server == h && type == "DIS") continue;

        update_ips_state(tc);
        if (type == "DIS")
        {
            int k = get_ip_by_owner(client);
            if (!k) k = get_ip_by_state(0);
            if (!k) k = get_ip_by_state(3);
            if (!k) continue;
            ip[k].state = 1, ip[k].owner = client;
            if (!te) ip[k].t = tc + t_def;
            else
            {
                int t = te - tc;
                t = max(t, t_min), t = min(t, t_max);
                ip[k].t = tc + t;
            }
            cout << h << ' ' << client << ' ' << "OFR" << ' ' << k << ' ' << ip[k].t << endl;
        }
        else
        {
            if (server != h)
            {
                for (int i = 1; i <= n; i ++ )
                    if (ip[i].owner == client && ip[i].state == 1)
                    {
                        ip[i].state = 0;
                        ip[i].owner = "";
                        ip[i].t = 0;
                    }
                continue;
            }
            if (!(id >= 1 && id <= n && ip[id].owner == client))
                cout << h << ' ' << client << ' ' << "NAK" << ' ' << id << ' ' << 0 << endl;
            else
            {
                ip[id].state = 2;
                if (!te) ip[id].t = tc + t_def;
                else
                {
                    int t = te - tc;
                    t = max(t, t_min), t = min(t, t_max);
                    ip[id].t = tc + t;
                }
                cout << h << ' ' << client << ' ' << "ACK" << ' ' << id << ' ' << ip[id].t << endl;
            }
        }
    }

    return 0;
}

第23次

第2题非零段划分

思维题
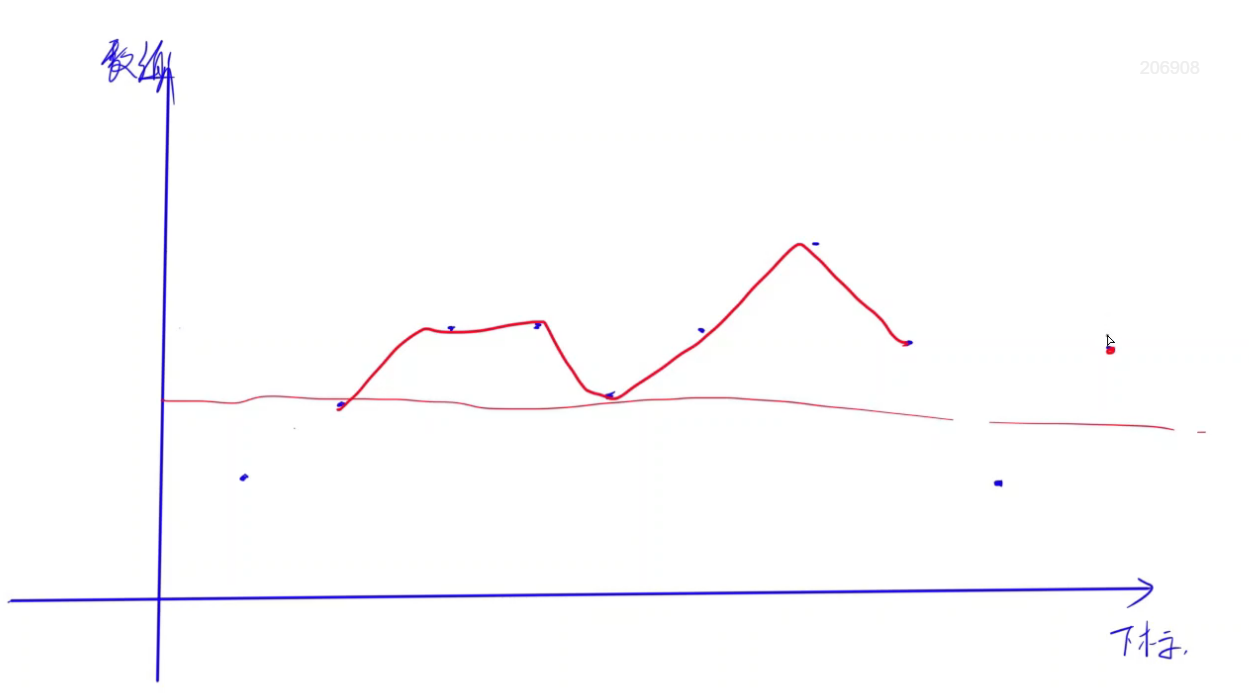
模拟：在基准线不断下沉的过程中，有多少段小山峰。
如下图所示有两端小山峰：

规则：

从大到小露出，高度越高的先露出来
相邻相同的山峰可以看成一个整体
- 可以去重
山峰种类：
- 突起：山峰+1
- 左边山峰右边没有山峰(或反)：山峰延长，数量不变
- 山谷：山峰-1，左右两边连在一块
统计每种高度的山峰数量即可

山峰种类

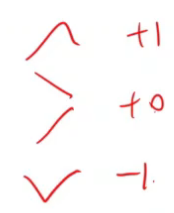
法1：

最大值则只需要从其前缀和（程序中实际为后缀和）中找出最大值

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 500010, M = 10010;

int n;
int a[N], cnt[M];

int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);
    n = unique(a + 1, a + n + 1) - a - 1;		// 去重
    a[0] = a[n + 1] = 0;

    for (int i = 1; i <= n; i ++ )
    {
        int x = a[i - 1], y = a[i], z = a[i + 1];
        // cnt[i] 表示海平面下降到 i 时，岛屿数量的变化
        if (x < y && z < y) cnt[y] ++ ;
        else if (x > y && z > y) cnt[y] -- ;
    }

    int res = 0, sum = 0;
    for (int i = M - 1; i; i -- )		// 从高到低进行枚举
    {
        sum += cnt[i];
        res = max(res, sum);
    }

    printf("%d\n", res);
    return 0;
}

法2：前缀和，时间复杂度O(n)

如果a[i] > a[i − 1]，意味着当p取到a[i − 1] + 1到a[i]之间的值时，非零段+1

使用数组cnt[]，cnt[i] 表示p从i - 1上升到i时，非零段数量的变化

从正向前缀和中找出最大值就是所要的结果

#include <iostream>
using namespace std;

const int N = 500004;
const int M = 10004;
int a[N], cnt[N];

int main()
{
    int n, phrase = 0; // 整数个数，段数
    int i;

    cin >> n;
    for(i = 1; i <= n; i++)
    {
        scanf("%d", &a[i]);
        if(a[i] > a[i-1])
        {
            cnt[a[i-1]+1]++;
            cnt[a[i]+1]--;
        }
    }

    int sum = 0;
    for(i = 1; i < M; i++)
    {
        sum += cnt[i];
        phrase = max(phrase, sum);
    }

    printf("%d\n", phrase);
    return 0;
}

第24次

第2题序列查询新解

可以先按照 $f$ 分段，再按照 $g$ 分段

$f(x)$ 表示序列 $A$ 中小于等于 $x$ 的整数里最大的数的下标，则 $f(x)$ 值为 $i$ 的 $x$ 的取值范围为 $[a[i],a[i+1]-1]$

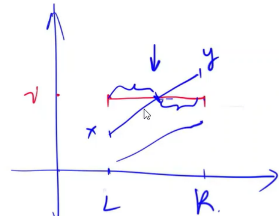
而 $g$ 是一个分段上升的函数，在 $[a[i],a[i+1]-1]$ 区间内以每 $r$ 个数一个值的速度上升。我们计算 $\sum_{i=0}^{N-1}|f(x)-g(x)|$，可以分为三种情况：

$f(x)$ 恒大于等于 $g(x)$
$f(x)$ 恒小于等于 $g(x)$
$g(x)$ 穿过 $f(x)$

计算 $g(x)$ 在区间中的和可分为三段：中间部分 + 左边界 + 右边界，计算中间部分的起始值 $a,b$ 为：$a = l / R + 1, b = r / R - 1$，可用等差数列求和公式计算和。

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

typedef long long LL;

const int N = 100010;

int n, m;
int a[N];
int R;

LL get(int l, int r)  // 求g[l] + g[l + 1] + ... + g[r]
{
    if (l / R == r / R) return (LL)(r - l + 1) * (l / R);
    int a = l / R + 1, b = r / R - 1;
    LL res = (a + b) * (LL)(b - a + 1) / 2 * R;  // 中间部分
    res += (a - 1) * (LL)(a * R - l);  // 左边界
    res += (b + 1) * (LL)(r - (b * R + R) + 1);  // 右边界
    return res;
}

int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);
    a[n + 1] = m;
    R = m / (n + 1);

    LL res = 0;
    for (int i = 0; i <= n; i ++ )
    {
        int l = a[i], r = a[i + 1] - 1;
        int x = l / R, y = r / R;
        if (y <= i || x >= i)
        {
            res += abs((LL)i * (r - l + 1) - get(l, r));
        }
        else
        {
            int mid = i * R;	// 值为i的g[n]的下标最小值
            res += abs((LL)i * (mid - l + 1) - get(l, mid));  // 左半边
            res += abs((LL)i * (r - mid) - get(mid + 1, r));  // 右半边
        }
    }

    printf("%lld\n", res);
    return 0;
}

第25次

第3题计算资源调度器)

50分

#include<iostream>
#include<algorithm>

using namespace std;

const int N = 1010;
struct Node
{
    int u;    // 所属编号
    int w;    // 任务数量
    int s;    // 序号
    bool operator< (const Node &W)const
    {
        if(w == W.w)
            return s < W.s;
        return w < W.w;
    }
}a[N];        // 计算节点

int main()
{
    int n, m, group;
    scanf("%d%d", &n, &m);
    for(int i = 0; i < n; i++)
    {
        scanf("%d", &a[i].u);
        a[i].s = i + 1;
        a[i].w = 0;
    }
    scanf("%d", &group);
    while(group --)
    {
        int f, k, b, c, d, e;
        scanf("%d%d%d%d%d%d", &f, &k, &b, &c, &d, &e);
        while(f--)
        {
            sort(a, a + n);
            if(b == 0)
            {
                printf("%d ", a[0].s);
                a[0].w ++;
            }
            else
            {
                int i = 0;
                while(a[i].u != b && i < n)
                {
                    i++;
                }
                if(i == n) printf("0 ");
                else
                {
                    printf("%d ", a[i].s);
                    a[i].w ++;
                }
            }
        }
        printf("\n");
    }
    return 0;
}

第26次

第2题寻宝！大冒险！

运用到pair、map数据结构，多加注意map的用法
暴力遍历数组，二重循环，通过mp[{dx + i, dy + j}] != rp[{i, j}]判断

#include<bits/stdc++.h>

using namespace std;

int n, l, s;
typedef pair<int, int> PII;
map<PII, int> mp;
map<PII, int> rp;
vector<PII> qwe;

int main()
{
	scanf("%d%d%d", &n, &l, &s);
	//利用map读取数据
	for (int i = 0; i < n; i++)
	{
		int first, second;
		scanf("%d%d", &first, &second);
		mp[{first, second}] = 1;
		qwe.push_back({ first,second });
	}

	for (int i = s; i >= 0; i--)
	{
		for (int j = 0; j <= s; j++)
		{
			int x;
			scanf("%d", &x);
			rp[{i, j}] = x;
		}
	}

	int count = 0;
	for (int r = 0; r < qwe.size(); r++)
	{
		int dx = qwe[r].first, dy = qwe[r].second;
		bool flag = true;
		for (int i = 0; i <= s; i++)
		{
			for (int j = 0; j <= s; j++)
			{
				if (mp[{dx + i, dy + j}] != rp[{i, j}] || dx + i > l || dy + j > l)
				{
					flag = false;
					break;
				}
			}
			if (!flag)
			{
				break;
			}
		}
		if (flag) count++;		//该点满足题意
	}

	printf("%d\n", count);
	return 0;
}

ShiQuLiZhi

https://www.qqzzss.top/2022/09/21/algorithmlearning/suan-fa-shua-ti-csp-kao-shi-shua-ti-ji-lu/

本博客所有文章除特别声明外，均采用 CC BY 4.0 许可协议。转载请注明来源 ShiQuLiZhi !

算法程序设计

算法课外思考题0923(众数与求和)

2022-09-23 作业

算法程序设计

机试算法刷题记录

2022-09-21 算法学习

算法程序设计

CSP考试刷题记录

第0次

第4题 有趣的数

第1次

第3题 命令行选项

第3次

第3题 集合竞价

第4次

第3题 节日

第16次

第2题 二十四点)

第18次

第3题 化学方程式

第21次

第2题 期末预测之最佳阈值

第22次

第2题 邻域均值

第3题 DHCP服务器

第23次

第2题 非零段划分

第24次

第2题 序列查询新解

第25次

第3题 计算资源调度器)

50分

第26次

第2题 寻宝！大冒险！

第4题有趣的数

第3题命令行选项

第3题集合竞价

第3题节日

第2题二十四点)

第3题化学方程式

第2题期末预测之最佳阈值

第2题邻域均值

第2题非零段划分

第2题序列查询新解

第3题计算资源调度器)

第2题寻宝！大冒险！