机试算法刷题记录

1.[类动规划分]截断数组

给定一个长度为 $n$ 的数组 $a_1,a_2,…,a_n$。现在，要将该数组从中间截断，得到三个非空子数组。

要求，三个子数组内各元素之和都相等。请问，共有多少种不同的截断方法？

• 因为要把数组均分三份，总和一定得是3的倍数

• 遍历前缀和数组，边扫描边记录哪些地方可以切第一刀，哪些地方可以切第二刀。如果位置j可以切第二刀，那么它与前面第一刀进行组合

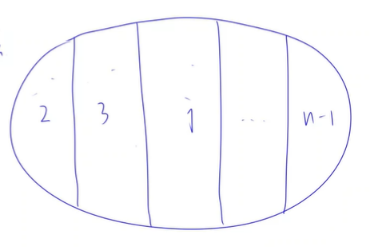
根据第二刀的位置划分出 $n$ 种情况。

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

typedef long long LL;

const int N = 100010;

int n;
int s[N];

int main()
{
    scanf("%d", &n);
    for(int i = 1; i <= n; i ++ )
    {
        int x;
        scanf("%d", &x);
        s[i] = s[i - 1] + x;
    }

    if (s[n] % 3) puts("0");
    else
    {
        LL res = 0, cnt = 0;
        for (int j = 2; j < n; j ++ )
        {
            if (s[j - 1] == s[n] / 3) cnt ++ ;
            if (s[j] == s[n] / 3 * 2) res += cnt;
        }

        printf("%lld\n", res);
    }

    return 0;
}

2.[差分]改变数组元素

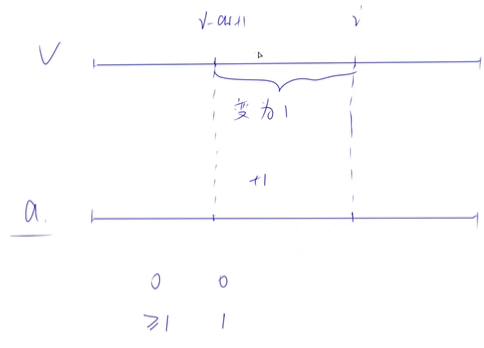
a 数组表示 v 数组各个元素的操作次数。当 a 数组元素操作次数 $\geq 1$ 时， v 数组元素的值为 $1$。

可以运用差分算法进行操作。

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 200010;

int n;
int b[N];

int main()
{
    int T;
    scanf("%d", &T);
    while (T -- )
    {
        scanf("%d", &n);
        memset(b, 0, (n + 1) * 4);		// int为4个字节
        for (int i = 1; i <= n; i ++ )
        {
            int x;
            scanf("%d", &x);
            x = min(x, i);
            int l = i - x + 1, r = i;
            b[l] ++, b[r + 1] -- ;
        }
        for (int i = 1; i <= n; i ++ ) b[i] += b[i - 1];
        for (int i = 1; i <= n; i ++ ) printf("%d ", !!b[i]);	// !!表示int转bool
        puts("");
    }

    return 0;
}

3.[二分+哈希]我在哪？

找到最小的 $K$，使得任意两个长度为 $K$ 的子串都不相同。

能否二分—->是否具有二段性

二分 + STL Set(哈希表) $O(n^2logn)$

#include <iostream>
#include <cstring>
#include <algorithm>
#include <unordered_set>

using namespace std;

int n;
string str;
unordered_set<string> S;

bool check(int mid)
{
    S.clear();
    for (int i = 0; i + mid - 1 < n; i ++ )
    {
        string s = str.substr(i, mid);
        if (S.count(s)) return false;
        S.insert(s);
    }

    return true;
}

int main()
{
    cin >> n >> str;

    int l = 1, r = n;
    while (l < r)
    {
        int mid = l + r >> 1;
        if (check(mid)) r = mid;
        else l = mid + 1;
    }

    cout << r << endl;

    return 0;
}

4.[二分]垦田计划

#include <bits/stdc++.h>
 
using namespace std;
using ll = long long;
 
constexpr int N = 1e5 + 10;
int n, m, k, mx = -1;
pair<int, int> a[N];
 
int check(int x) {
    int cos = 0;
    for (int i = 1; i <= n; i++) {
        if (a[i].first >= x) 
            cos += (a[i].first - x) * a[i].second;
        else
            break;
    }
    return cos <= m;
}
 
int main()
{  
    cin >> n >> m >> k;
 
    for (int i = 1; i <= n; i++) {
        cin >> a[i].first >> a[i].second;
        mx = max(mx, a[i].first);
    }
    
    sort(a + 1, a + 1 + n, [&](const pair<int, int> &x, const pair<int, int> &y) {
        return x.first > y.first;
    });
 
    int l = k, r = mx;
    while (l < r) {
        int mid = (l + r) >> 1;
        if (check(mid)) r = mid;
        else l = mid + 1;
    }
 
    cout << l << "\n";
    
    return 0;
}

5.[二分/哈希]四平方和

四平方和定理，又称为拉格朗日定理：

每个正整数都可以表示为至多 $4$ 个正整数的平方和。

如果把 $0$ 包括进去，就正好可以表示为 $4$ 个数的平方和。

比如：

$5=0^2 +0^2+1^2+2^2$
$7=1^2+1^2+1^2+2^2$

对于一个给定的正整数，可能存在多种平方和的表示法。

要求你对 $4$ 个数排序：

$0≤a≤b≤c≤d$

并对所有的可能表示法按 $a,b,c,d$ 为联合主键升序排列，最后输出第一个表示法。

如果找到字典序最小的解—->存到结构体中并排序，找到 $t=n-a^2-b^2$字典序最小的组合

“查询$c^2+d^2$的值的结果是否存在”

二分 $O(N^2logN)$

#include <cstring>
#include <iostream>
#include <algorithm>
#include <cmath>

using namespace std;

const int N = 2500010;

struct Sum
{
    int s, c, d;
    bool operator< (const Sum &t)const
    {
        if (s != t.s) return s < t.s;
        if (c != t.c) return c < t.c;
        return d < t.d;
    }
}sum[N];

int n, m;

int main()
{
    cin >> n;

    for (int c = 0; c * c <= n; c ++ )
        for (int d = c; c * c + d * d <= n; d ++ )
            sum[m ++ ] = {c * c + d * d, c, d};

    sort(sum, sum + m);

    for (int a = 0; a * a <= n; a ++ )
        for (int b = 0; a * a + b * b <= n; b ++ )
        {
            int t = n - a * a - b * b;
            int l = 0, r = m - 1;
            while (l < r)
            {
                int mid = l + r >> 1;
                if (sum[mid].s >= t) r = mid;
                else l = mid + 1;
            }
            if (sum[l].s == t)
            {
                printf("%d %d %d %d\n", a, b, sum[l].c, sum[l].d);
                return 0;
            }
        }

    return 0;
}

哈希表 $O(N^2)$（仅理论，哈希表 STL 常数大，时间复杂度高）

#include <cstring>
#include <iostream>
#include <algorithm>
#include <unordered_map>

#define x first
#define y second

using namespace std;

typedef pair<int, int> PII;

const int N = 2500010;

int n, m;
unordered_map<int, PII> S;

int main()
{
    cin >> n;

    for (int c = 0; c * c <= n; c ++ )
        for (int d = c; c * c + d * d <= n; d ++ )
        {
            int t = c * c + d * d;
            if (S.count(t) == 0) S[t] = {c, d};		// 字典序最小
        }

    for (int a = 0; a * a <= n; a ++ )
        for (int b = 0; a * a + b * b <= n; b ++ )
        {
            int t = n - a * a - b * b;
            if (S.count(t))
            {
                printf("%d %d %d %d\n", a, b, S[t].x, S[t].y);
                return 0;
            }
        }

    return 0;
}

6.[二分]分巧克力

需满足不等式关系：$\sum_{i=0}^{n-1}\left\lfloor\frac{h_{1}}{\text { mid }}\right\rfloor \cdot\left\lfloor\frac{w_{j}}{\text { mid }}\right\rfloor<k$

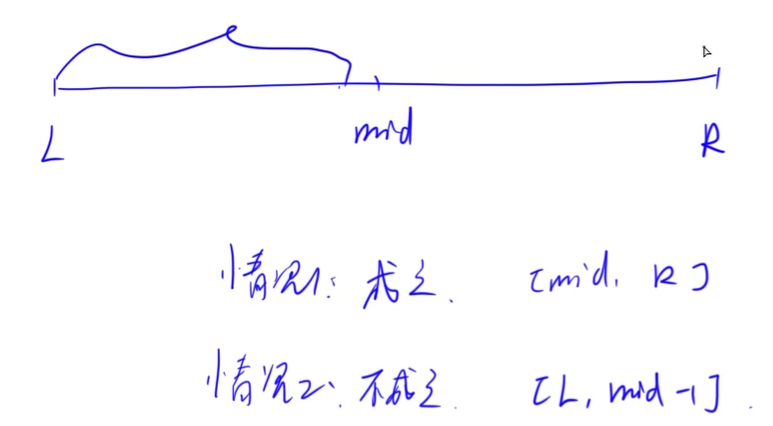
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 100010;

int n, k;
int h[N], w[N];

bool check(int mid)
{
    int res = 0;
    for (int i = 0; i < n; i ++ )
    {
        res += (h[i] / mid) * (w[i] / mid);
        if (res >= k) return true;
    }

    return false;
}

int main()
{
    scanf("%d%d", &n, &k);
    for (int i = 0; i < n; i ++ ) scanf("%d%d", &h[i], &w[i]);

    int l = 1, r = 1e5;
    while (l < r)
    {
        int mid = l + r + 1 >> 1;
        if (check(mid)) l = mid;
        else r = mid - 1;
    }

    printf("%d\n", r);

    return 0;
}

7.[DP]接龙数列

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 100010;

int n;
int g[10];

int main()
{
    scanf("%d", &n);

    int res = 0;
    char num[20];
    for (int i = 0; i < n; i ++ )
    {
        scanf("%s", num);
        int l = num[0] - '0', r = num[strlen(num) - 1] - '0';
        int f = max(1, g[l] + 1);
        g[r] = max(g[r], f);
        res = max(res, f);
    }

    printf("%d\n", n - res);
    return 0;
}

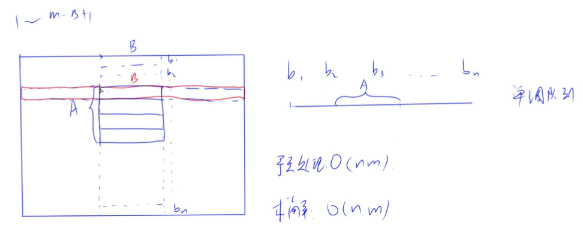
8.[滑动窗口]子矩阵

考察单调队列：

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

typedef long long LL;
const int N = 1010, MOD = 998244353;

int n, m, A, B;
int w[N][N];
int rmax[N][N], rmin[N][N];
int q[N];

void get_max(int a[], int b[], int tot, int k)
{
    int hh = 0, tt = -1;
    for (int i = 0; i < tot; i ++ )
    {
        if (hh <= tt && q[hh] <= i - k) hh ++ ;			// 判断队头是否滑出窗口
        while (hh <= tt && a[q[tt]] <= a[i]) tt -- ;
        q[ ++ tt] = i;
        b[i] = a[q[hh]];		// 当前滑动窗口的最大值
    }
}

void get_min(int a[], int b[], int tot, int k)
{
    int hh = 0, tt = -1;
    for (int i = 0; i < tot; i ++ )
    {
        if (hh <= tt && q[hh] <= i - k) hh ++ ;
        while (hh <= tt && a[q[tt]] >= a[i]) tt -- ;
        q[ ++ tt] = i;
        b[i] = a[q[hh]];
    }
}

int main()
{
    scanf("%d%d%d%d", &n, &m, &A, &B);
    for (int i = 0; i < n; i ++ )
        for (int j = 0; j < m; j ++ )
            scanf("%d", &w[i][j]);

    for (int i = 0; i < n; i ++ )
    {
        get_max(w[i], rmax[i], m, B);		// 对每行的每个滑动窗口进行单调队列计算
        get_min(w[i], rmin[i], m, B);
    }

    int res = 0;

    int a[N], b[N], c[N];
    
    // 求长度为 A 的窗口的最值 
    for (int i = B - 1; i < m; i ++ )
    {
        for (int j = 0; j < n; j ++ ) a[j] = rmax[j][i];	// 复制出每行最大值
        get_max(a, b, n, A);
        for (int j = 0; j < n; j ++ ) a[j] = rmin[j][i];	// 复制出每行最小值
        get_min(a, c, n, A);
        for (int j = A - 1; j < n; j ++ )
            res = (res + (LL)b[j] * c[j]) % MOD;
    }

    printf("%d\n", res);
    return 0;
}

9.[高精度]10进制 VS 2进制

秦九韶算法

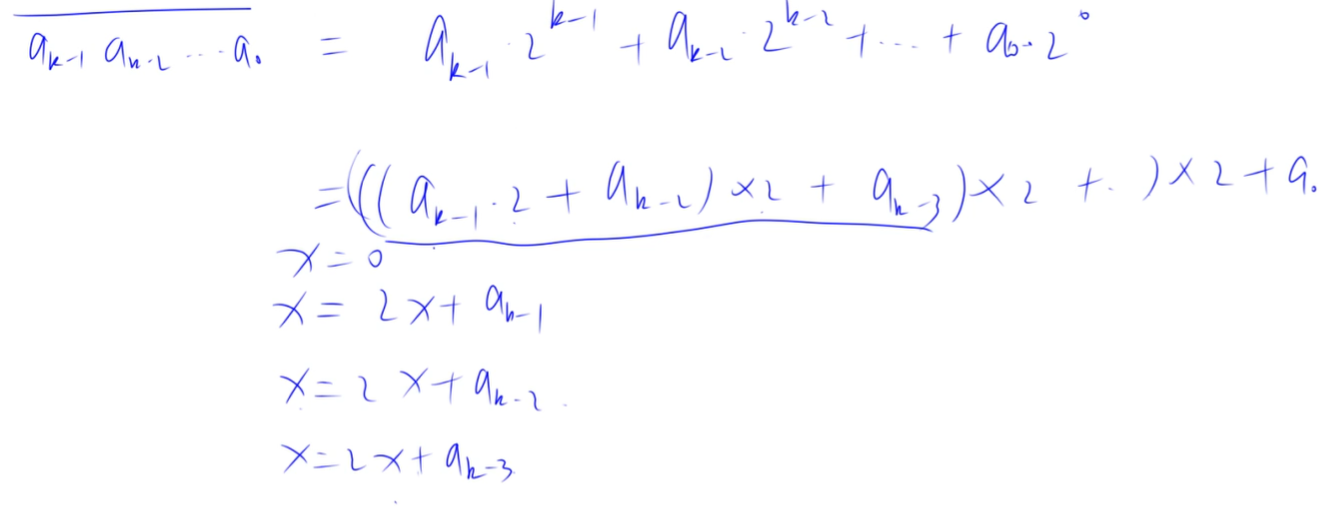
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>

using namespace std;

vector<int> div(vector<int>& A, int b, int& r)
{
    vector<int> C;
    r = 0;
    for (int i = A.size() - 1; i >= 0; i -- )
    {
        r = r * 10 + A[i];
        C.push_back(r / b);
        r %= b;
    }
    reverse(C.begin(), C.end());
    while (C.size() > 1 && C.back() == 0) C.pop_back();
    return C;
}

vector<int> mul(vector<int>& A, int b)
{
    vector<int> C;
    for (int i = 0, t = 0; i < A.size() || t; i ++ )
    {
        if (i < A.size()) t += A[i] * b;
        C.push_back(t % 10);
        t /= 10;
    }

    while (C.size() > 1 && C.back() == 0) C.pop_back();
    return C;
}

vector<int> add(vector<int>& A, int b)
{
    vector<int> C;
    for (int i = 0, t = b; i < A.size() || t; i ++ )
    {
        if (i < A.size()) t += A[i];
        C.push_back(t % 10);
        t /= 10;
    }
    return C;
}

void print(vector<int>& A)
{
    for (int i = A.size() - 1; i >= 0; i -- )
        cout << A[i];
    cout << endl;
}

int main()
{
    string a;
    cin >> a;

    vector<int> A;
    for (int i = a.size() - 1; i >= 0; i -- ) A.push_back(a[i] - '0');

    vector<int> B;
    while (A.size() > 1 || A[0] > 0)
    {
        int r;
        A = div(A, 2, r);		// 每次除以2, 并记录余数
        B.push_back(r);			// 存的即为逆序
    }

    vector<int> C;
    for (int x: B)
    {
        C = mul(C, 2);
        C = add(C, x);
    }

    print(C);

    return 0;
}

10.[日期问题]日期差值

计算天的差值，只需分别计算其到公元1年1月1日的差即可。

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int months[] = {
    0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31
};

int is_leap(int year)
{
    if (year % 100 && year % 4 == 0 || year % 400 == 0)
        return 1;
    return 0;
}

int get_month_days(int year, int month)
{
    int res = months[month];
    if (month == 2) res += is_leap(year);
    return res;
}

int get_total_days(int y, int m, int d)
{
    int res = 0;
    for (int i = 1; i < y; i ++ )
        res += 365 + is_leap(i);

    for (int i = 1; i < m; i ++ )
        res += get_month_days(y, i);

    return res + d;
}

int main()
{
    int y1, m1, d1, y2, m2, d2;
    while (scanf("%04d%02d%02d", &y1, &m1, &d1) != -1)
    {
        scanf("%04d%02d%02d", &y2, &m2, &d2);
        printf("%d\n", abs(get_total_days(y1, m1, d1) - get_total_days(y2, m2, d2)) + 1);
    }

    return 0;
}

11.区间合并

class Solution {
    public int[][] merge(int[][] intervals) {
        /*
        贪心策略:
        1.按照左边界升序排序
        2.当intervals[i][0]<=intervals[i-1][1]时,说明能合并,更新intervals[i][1]=max(intervals[i][1],intervals[i-1][1])
        3.当intervals[i][0]>intervals[i-1][1]时,区间不重叠,将前面区间加入结果,更新新的左边界
        4.理论上最后一个结果不会加人,手动加入即可
         */
        List<int[]> list = new ArrayList<>();
        Arrays.sort(intervals, Comparator.comparingInt(a -> a[0]));
        // 每个重叠区间组左边界
        var len = intervals.length;
        int start = intervals[0][0];
        for (int i = 1; i < len; i++) {
            if (intervals[i][0] > intervals[i - 1][1]) {
                list.add(new int[]{start, intervals[i - 1][1]});
                // 更新区间组起点
                start = intervals[i][0];
            } else {
                // 更新区间组最大值,表示该区间组合并后的右边界
                intervals[i][1] = Math.max(intervals[i][1], intervals[i - 1][1]);
            }
        }
        // 添加最后一个区间(这使得区间数目为1也成立)
        list.add(new int[]{start, intervals[len - 1][1]});
        return list.toArray(new int[0][]);
    }
}