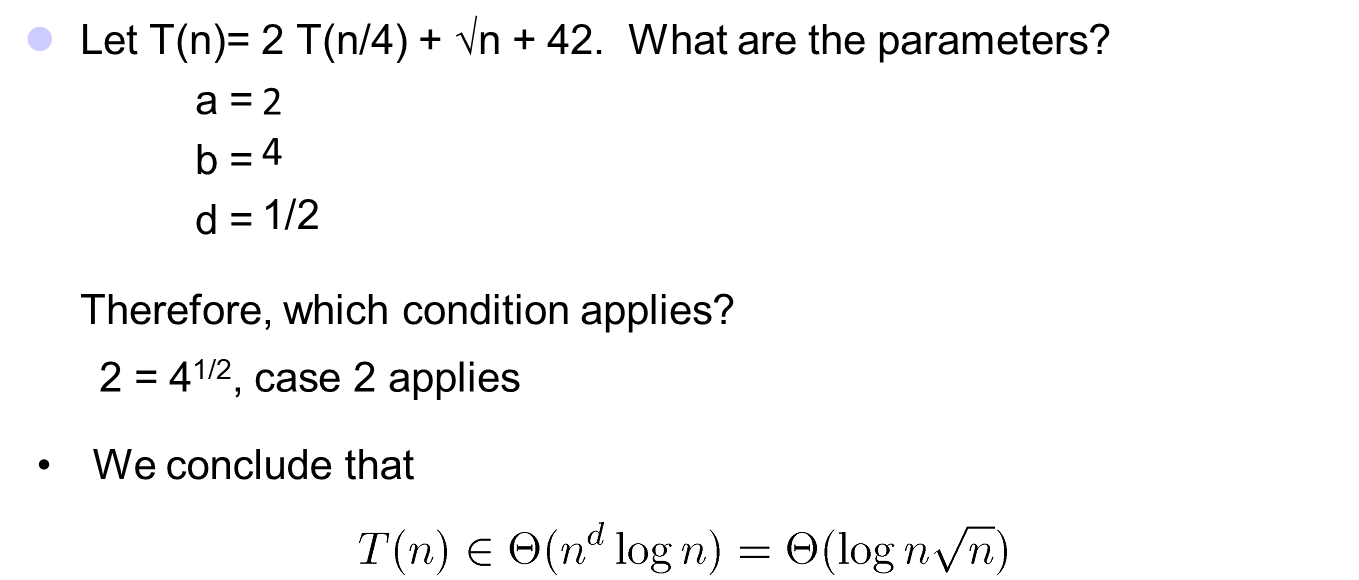前言:由数据范围反推算法复杂度以及算法内容
一般算法题的时间限制是1秒或2秒。在这种情况下,C++代码中的操作次数控制在 $10^7∼10^8$ 为最佳。
下面给出在不同数据范围下,代码的时间复杂度和算法该如何选择:
- $n≤30$, 指数级别,dfs+剪枝,状态压缩dp
- $n≤100$ => $O(n^3)$,floyd,dp,高斯消元
- $n≤1000$ => $O(n^2)$,$O(n^2logn)$,dp,二分,朴素版Dijkstra、朴素版Prim、Bellman-Ford
- $n≤10000$ => $O(n\sqrt n)$,块状链表、分块、莫队
- $n≤100000$ => $O(nlogn)$ => 各种sort,线段树、树状数组、set/map、heap、拓扑排序、dijkstra+heap、prim+heap、Kruskal、spfa、求凸包、求半平面交、二分、CDQ分治、整体二分、后缀数组、树链剖分、动态树
- $n≤1000000$ => $O(n)$, 以及常数较小的 $O(nlogn)$ 算法 => 单调队列、 hash、双指针扫描、并查集,kmp、AC自动机,常数比较小的 $O(nlogn)$ 的做法:sort、树状数组、heap、dijkstra、spfa
- $n≤10000000$ => $O(n)$,双指针扫描、kmp、AC自动机、线性筛素数
- $n≤10^9$ => $O(\sqrt n)$,判断质数
- $n≤10^{18}$ => $O(logn)$,最大公约数,快速幂,数位DP
- $n≤10^{1000}$ => $O((logn)^2)$,高精度加减乘除
- $n≤10^{100000}$ => $O(logk×loglogk)$,k表示位数,高精度加减、FFT/NTT
Tips:
- $log _2 10^n = 3n$
- 64MB至多开1600万个int
一、递归算法时间复杂度分析
1.1 替代法
1.1.1 数学归纳
猜测一种情况:
$T(n) = O(g(n))$
归纳目标:应用渐近符号的定义
- $T(n) ≤ d g(n)$, 对某些 $d > 0,n ≥ n_0$
归纳假设:$T(k) ≤ d g(k)$ (对任意$k < n$)
证明归纳目标:使用归纳假设找到常数$d$和$n_0$的某些值,归纳目标成立



1.1.2 待定系数
$T(1) = 1,T(n) = 4T(\frac{n}{2}) + n$,求时间复杂度。
待定系数法:$T(n) = an^2 + bn + c$
则$T(n) = an^2 + bn + c$,$4T(\frac{n}{2})+n = 4[a(\frac{n}{2})^2 + b(\frac{n}{2}) + c]+n=an^2+(2b+1)n+4c$,
故$T(n) = 2n^2-n$。
1.1.3 近似形式
$T(1) = 1$,$T(n) = aT(\frac{n}{b}) + f(n)$
Case1:若$aT(\frac{n}{b})<<f(n)$,则简化为$T(n)\approx f(n)$,则$T(n)=\Theta(f(n))$。
注:渐进符号:
$O(n)$表示上界,$\Omega(n)$表示下界,$\Theta(n)$表示精确情况。
Case2:若$aT(\frac{n}{b})>>f(n)$,则简化为$T(n)\approx aT(\frac{n}{b})$。
待定系数法:假定$T(n)=cn^{\alpha}$,则有:
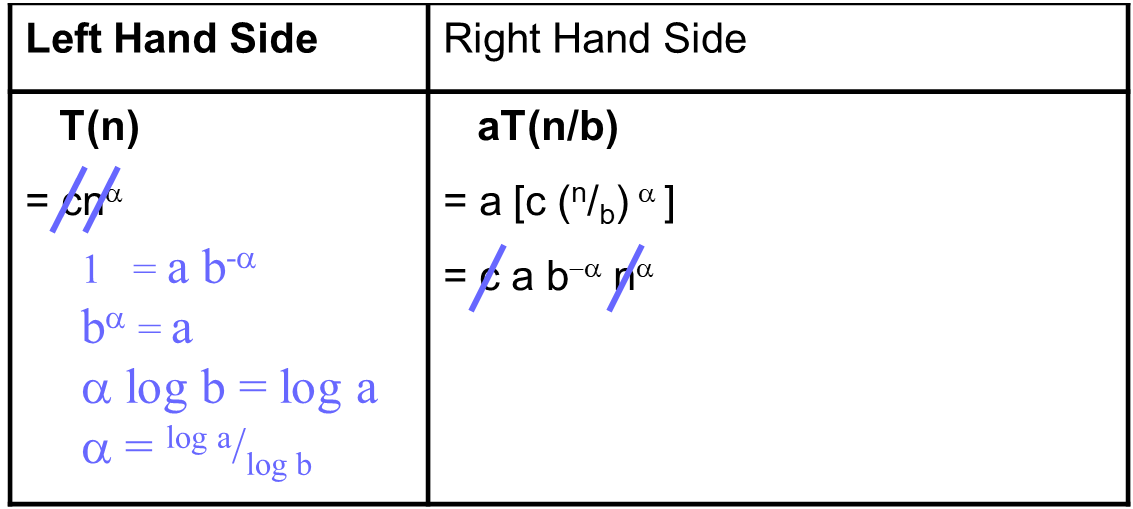
故$T(n) = \Theta (n^{log_a/log_b})$。
Case3:两部分时间复杂度相似,需使用下一种算法(递归树法)。
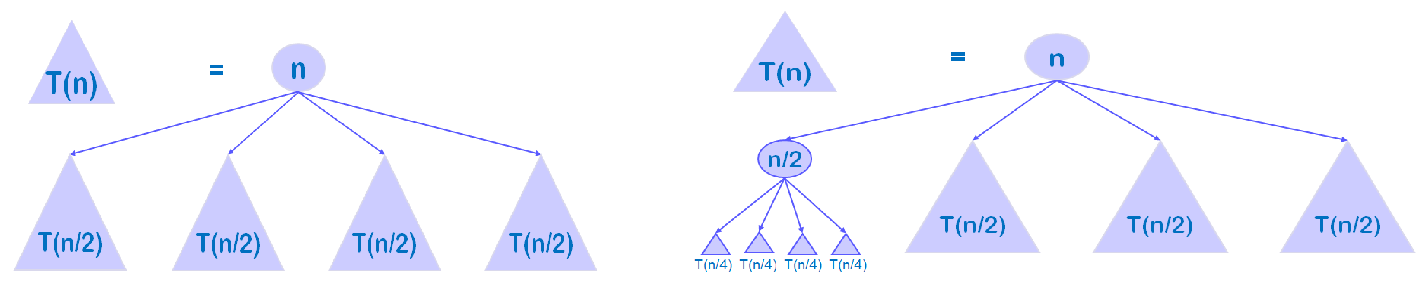
1.2 递归树法
Multiplication Algorithms:$T(n) = kT(n / b) + f(n)$
(1) 每层的节点为$T(n) = kT(n / b) + f(n)$中的$f(n)$在当前的$n/b$下的值;
(2) 每个节点的分支数为$k$。
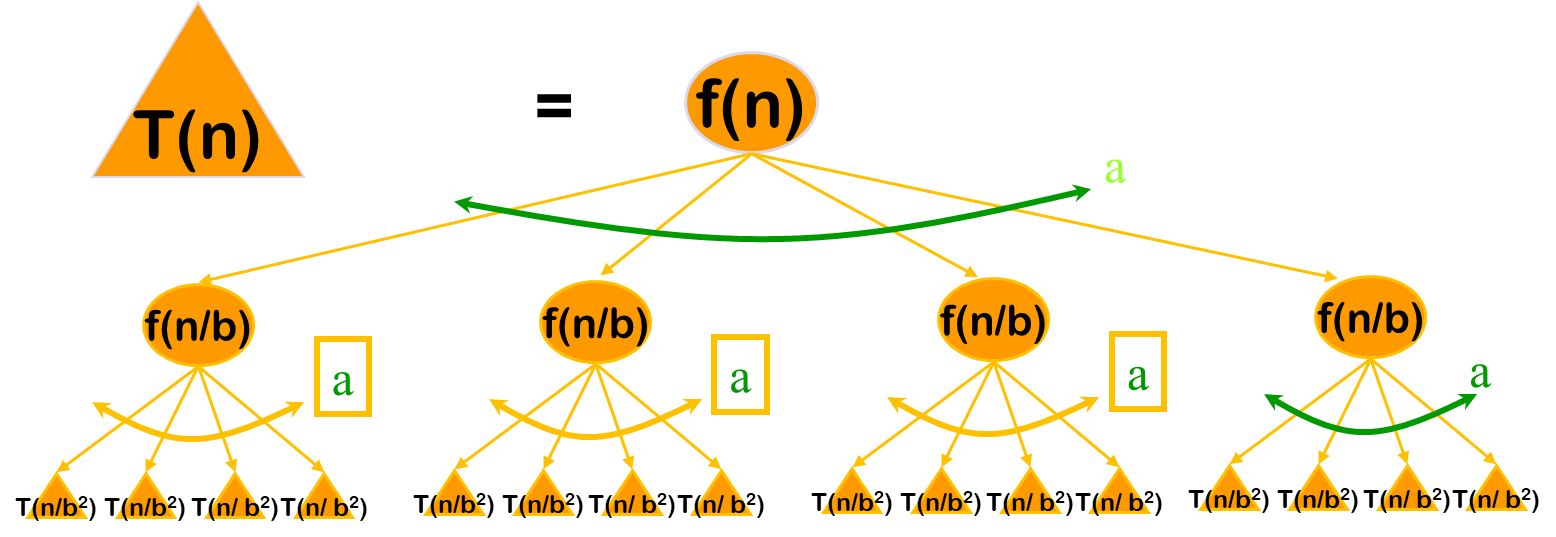
注:每棵子树代表$T(n/b) = f(n/b)+4T(n/b^2)$。
上图中,$T(n) = 4T(n/2)+n$。
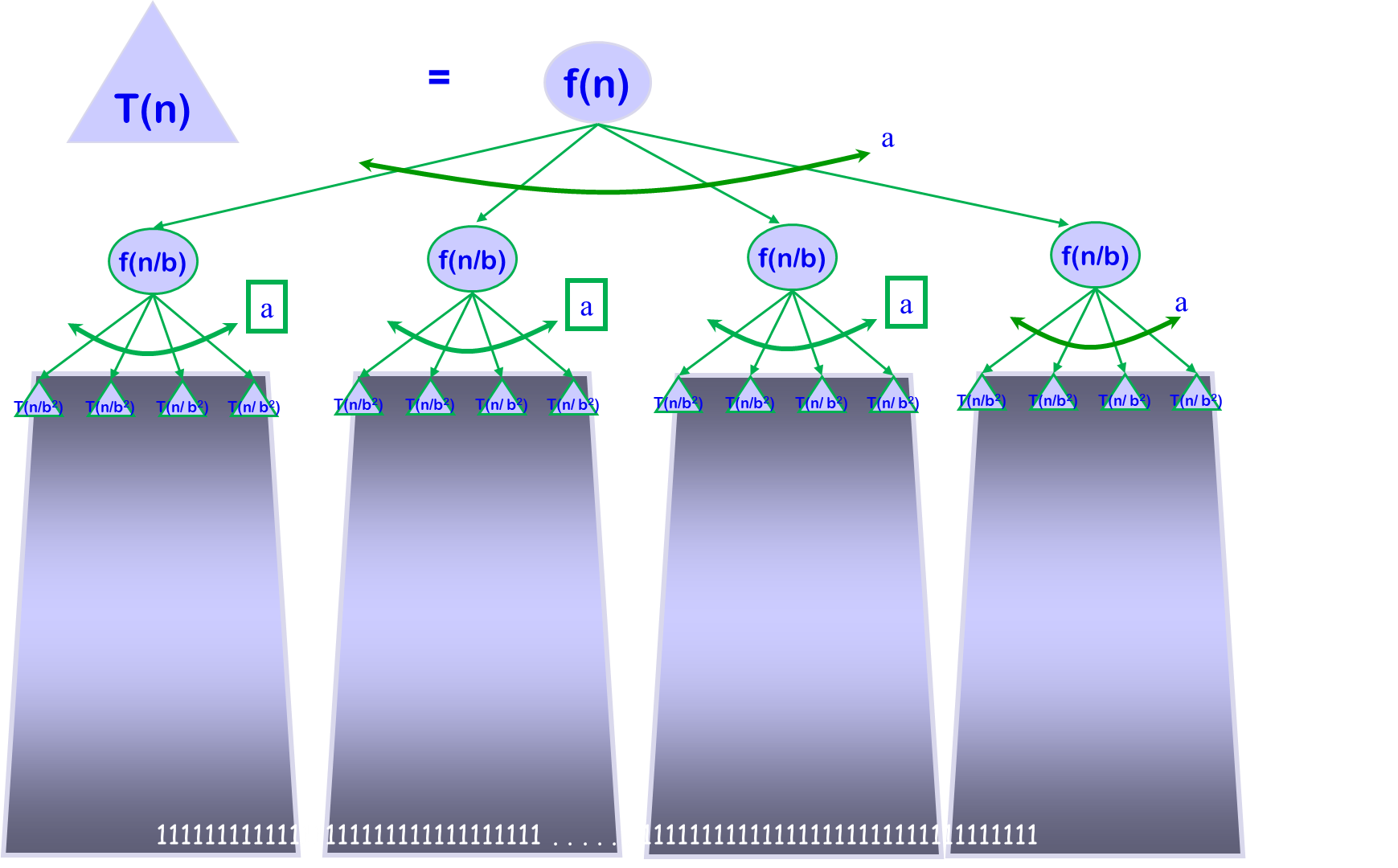
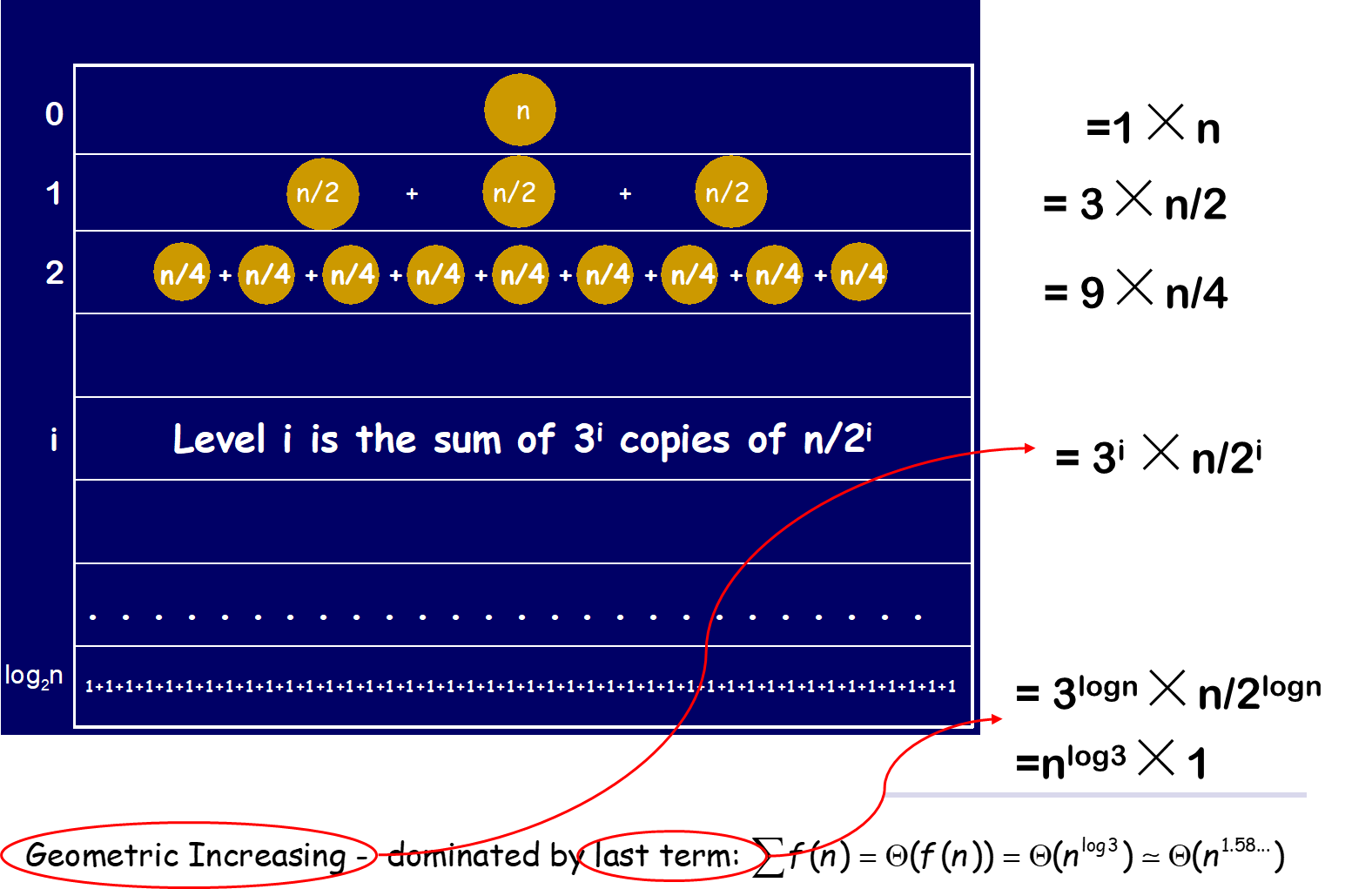
可以得到如下关系的表格:

树高算法:$b^h=n$,两边取对数,则有$hlogb=logn$,则$h=\frac{logn}{logb}$
$T(n)=\sum_{i=0 … h} a^{i} \times f\left(n / b^{i}\right)$
$\sum_{i=0 … n} x^{i}=\Theta(\max (\text { first term, last term }))$
注:如下图,$T(n)=3T(n/2)+n$呈几何增长时,时间复杂度取决于最后一项:
变式题1:
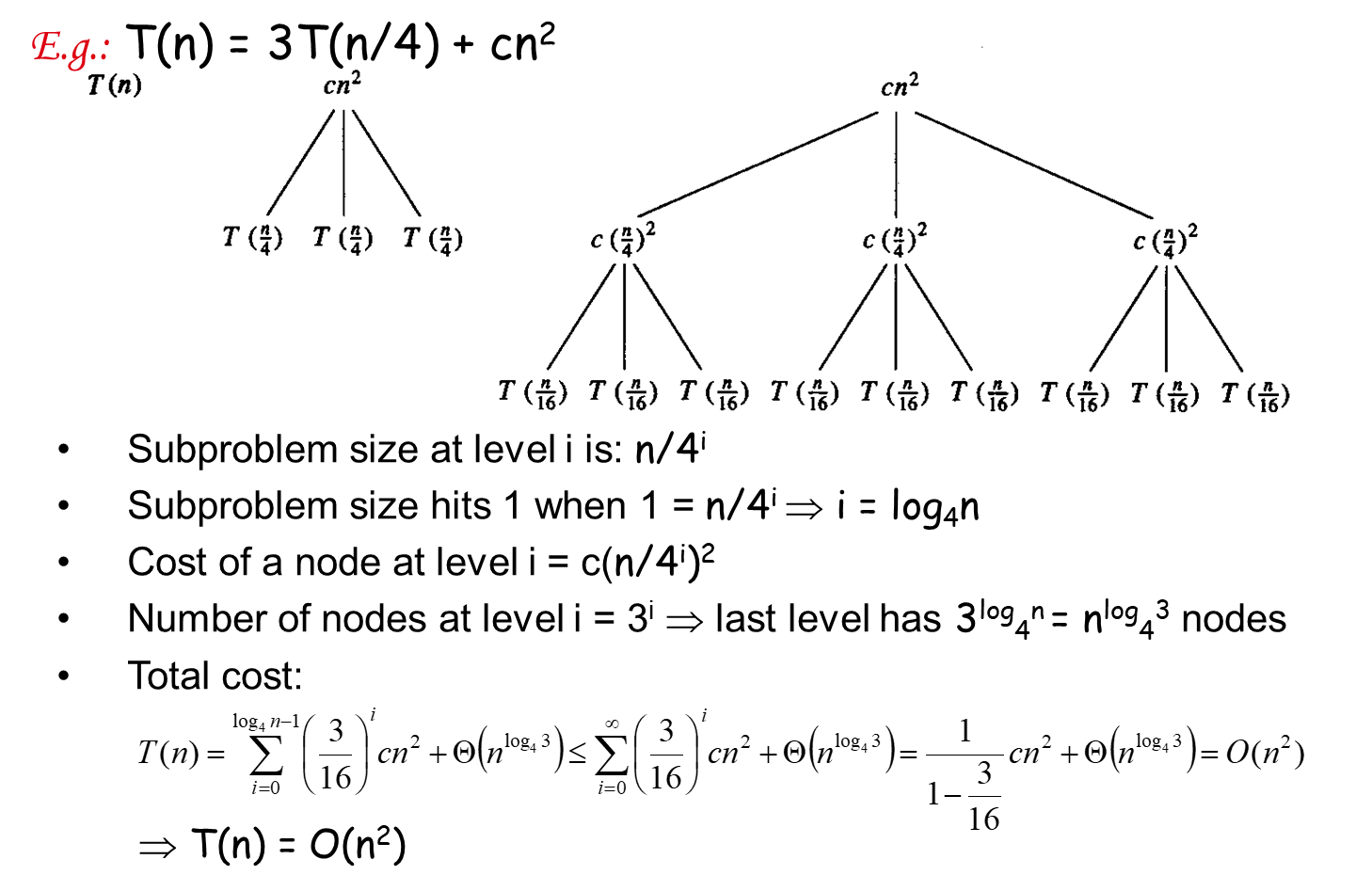
变式题2:
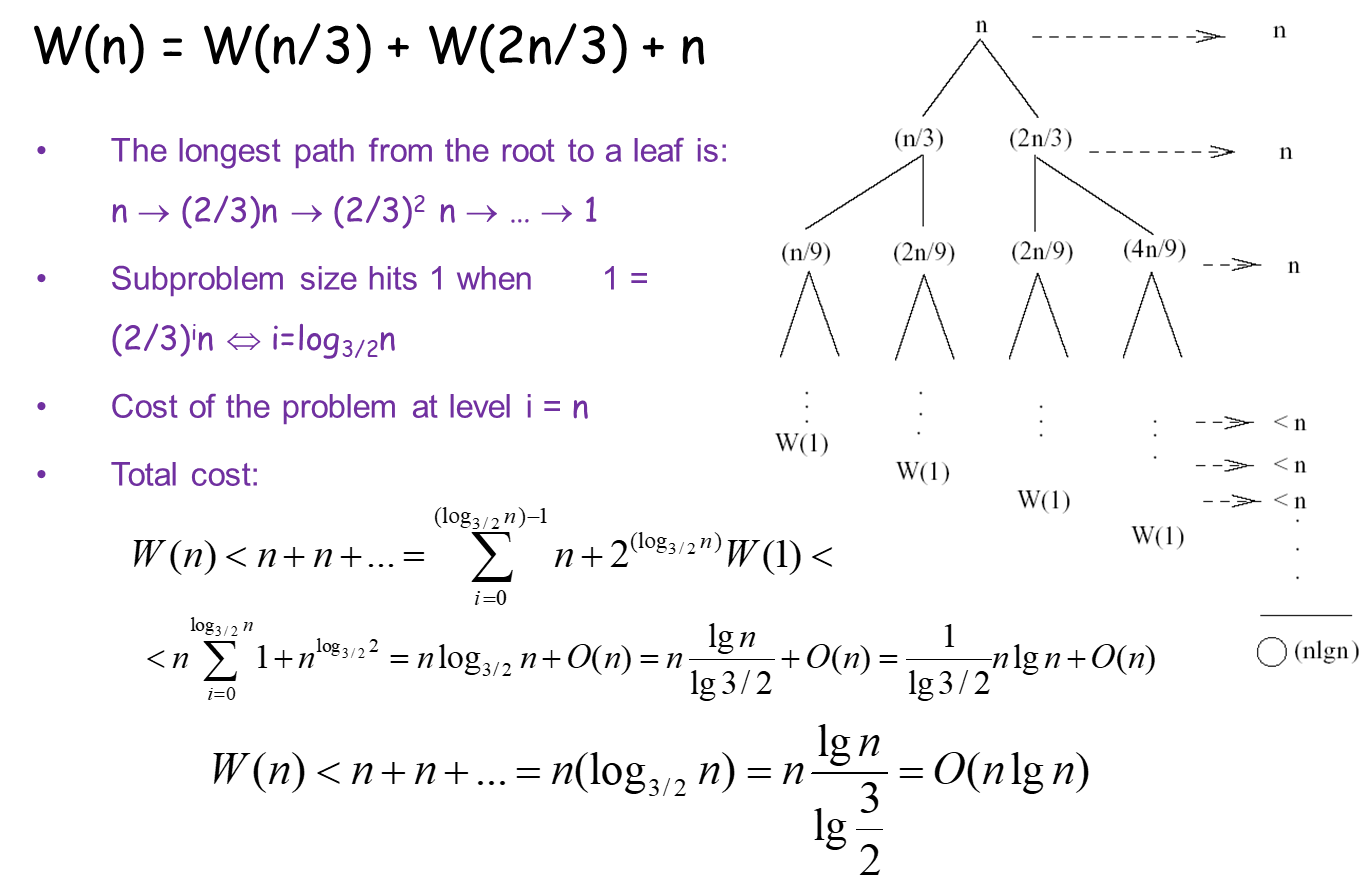
注:$\sum_{i=0}^{\left(\log _{3 / 2} n\right)-1} n+2^{\left(\log _{3 / 2} n\right)} W(1)$意即:将该树放缩为二叉树+出口条件的时间复杂度之和。
1.3 迭代法


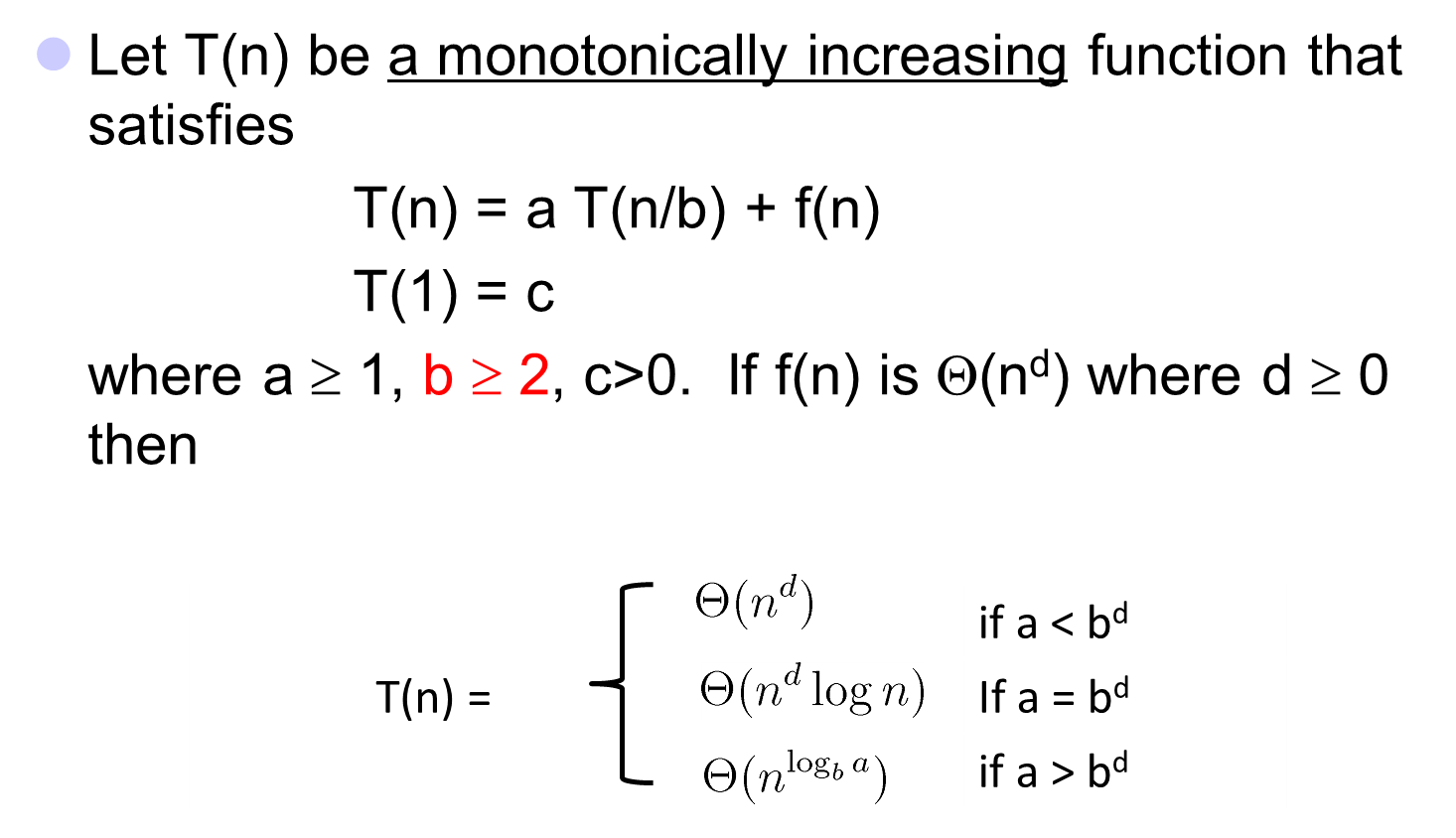
1.4 主定理(Master Theorem)法
主定理法用于解决以下迭代式:$T(n)=aT(\frac{n}{b})+f(n)$,其中$a\geq 1,b>1,f(n)>0$。
其中以下情况不能用主定理法求解:
$T(n)$不是单调的。e.g. $T(n) = sin(x)$
$f(n)$不是一个多项式。e.g. $T(n)=2T(n/2)+2^n$
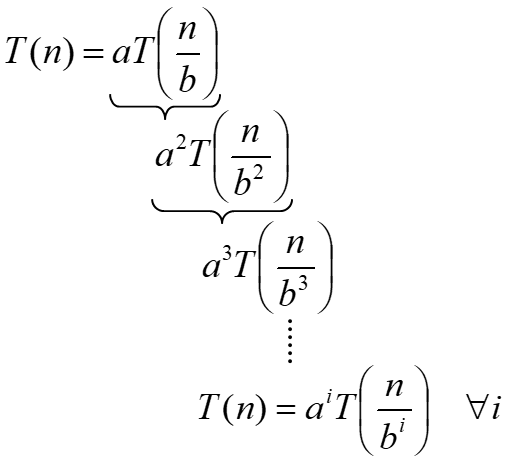
假设$n=b^k$,则$k=log_b n$。
当$i=k$(迭代到最后一层)时,有:$T(n)=a^{\log _{b} n} T\left(\frac{b^{i}}{b^{i}}\right)=a^{\log _{b} n} T(1)=\Theta\left(a^{\log _{b} n}\right)=\Theta\left(n^{\log _{b} a}\right)$
对于$T(n)=aT(\frac{n}{b})+f(n)$,将$f(n)$与$n^{\log _{b} a}$比较:
- $f(n)=O(n^{\log _{b} a}-\varepsilon)$(其中$\varepsilon>0$):$f(n)$的增长速度比$nlog_ba$的增长慢带有$n^{\varepsilon}$的多项式,则$T(n)=\Theta\left(n^{\log _{b} a}\right)$
- $f(n)=\Theta\left(n^{\log _{b} a} \lg ^{k} n\right)$(其中$k\geq 0$):$f(n)$与$n^{log_b a}$有较为相似的增长速度,则$T(n)=\Theta\left(n^{\log _{b} a} \lg ^{k+1} n\right)$
- $f(n)=\Omega\left(n^{\log _{b} a+\varepsilon}\right)$(其中$\varepsilon>0$):$f(n)$的增长速度将比$n^{log_ba}$快$n^{\varepsilon}$,且需满足存在一个$c(c<1)$,有$af(n/b)\leq cf(n)$,则$T(n)=\Theta(f(n))$。
[例1] $T(n) = 2T(n/2) + n,a = 2, b = 2, log_22 = 1.$
Compare $n^{log_22}$ with $f(n) = n$,有$f(n) = \Theta(n)$,满足Case 2,故$T(n) = \Theta(nlgn)$。
[例2]$T(n) = 2T(n/2) + n^2, a = 2, b = 2, log_22 = 1$.
Compare $n$ with $f(n) = n^2$,有$f(n) = \Omega(n^{1+\varepsilon})$,满足Case 3。
还需验证:$a f(n/b) ≤ c f(n) $,即$2 n^2/4 ≤ c n^2$ ,有$c = 1/2$ 满足要求($c<1$),故$T(n) = \Theta(n^2)$。
[例3]$T(n) = 3T(n/4) + nlgn,a = 3, b = 4, log_43 = 0.793.$
Compare $n^{0.793}$ with $f(n) = nlgn$,有$f(n) = \Omega(n^{log_43+\varepsilon})$,满足Case 3。
还需验证:$3*(n/4)lg(n/4) ≤ (3/4)nlgn = c *f(n), c=3/4$,故$T(n) = \Theta(nlgn)$。
更简单的情况:
主定理法的第四种情况:
$f(n)$不是多项式,但满足$f(n) \in \Theta\left(n^{\log _{b} a} \log ^{k} n\right)$,则$T(n) \in \Theta\left(n^{\log _{b} a} \log ^{k+1} n\right)$。
如$T(n)= 2 T(n/2) + n log n$,$a=2, b=2,f(n) \in \Theta(n \log n), k=1$,则有
$T(n) \in \Theta\left(n^{\log _{b} a} \log ^{k+1} n\right)=\Theta\left(n^{\log _{2} 2} \log ^{2} n\right)=\Theta\left(n \log ^{2} n\right)$
注:
该情况的使用条件是相当有限的,我们提出它只是为了介绍的完整性。
二、分治法(Divide&Conquer)
DQ(p)
{
if small(p) return S(p);
else
{
1. Divide p into smaller instances p1,p2,..,pk
2. Apply DQ to each pi
3. Return Combine(DQ(p1),DQ(p2),…,DQ(pk))
}
}将$g(n)$表示为当$p$较小时$S(p)$的时间复杂度,$f(n)$表示为拆分$p$并合并解决方案的时间复杂度,则:
当$p$较小时,$T(n)=g(n)$;否则有$T(n)=\sum_{i=1}^{k} T\left(n_{i}\right)+f(n)$
2.1 最近点对问题
一维:
排序+扫描:按照原点到各个点的距离进行排序,排序完成后只要进行一次扫描,将相邻点距离做一次计算即可。时间复杂度为$O(nlgn)+O(n)=O(nlgn)$(在时间性能要求比较高的情况下,可以采用基于位置的排序算法,时间复杂度为$O(dn)$)
D&Q算法:分治,找到两部分最小和中间部分最小的,三部分取
min,时间复杂度为$2T(n/2)+O(n)+O(1)$
二维:
利用D&Q算法,先找到两边的最小值,并以该最小值作为邻域。
对于SL虚框范围内的p点,我们可以画圆弧并进行比对;
注:
时间复杂度仍为$O(n^2)$,因为最坏情形下,在SR虚框中有可能会有$n/2$个点,对于SL虚框中的p点,每次要比较$n/2$次,浪费了算法的效率。
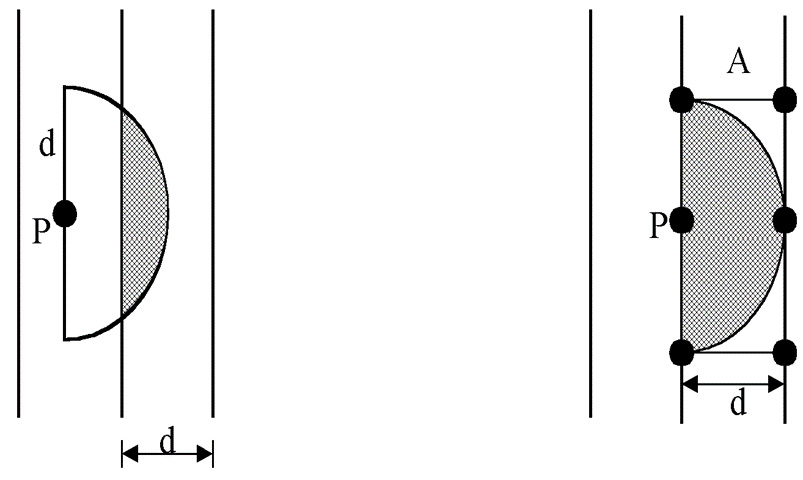
我们可以直接计算右图中的六个点:
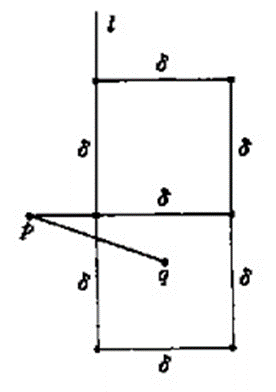
注:
$S_R$不会存在第七个点,若存在,右边的最小值不可能为$\delta$。时间复杂度将降为$O(n)$。
则该问题的时间复杂度为:
$\begin{array}{ll}
T(n)=\left{\begin{array}{ll}
2 T(n / 2)+O(n)+O(n) & , n>1 \
1 & , n=1
\end{array}\right. \
\Rightarrow T(n)=O(n \log n) &
\end{array}$
2.2 逆序对问题
2.2.1 树状数组求逆序对
给出一个长度为$n$的数组,完成以下两种操作:
- 将第$x$个数加上$k$
- 输出区间$[x,y]$内每个数的和
树状数组可以将单点修改和区间求和的运算的$n$次操作时间复杂度从$O(n^2)$降为$O(nlogn)$。
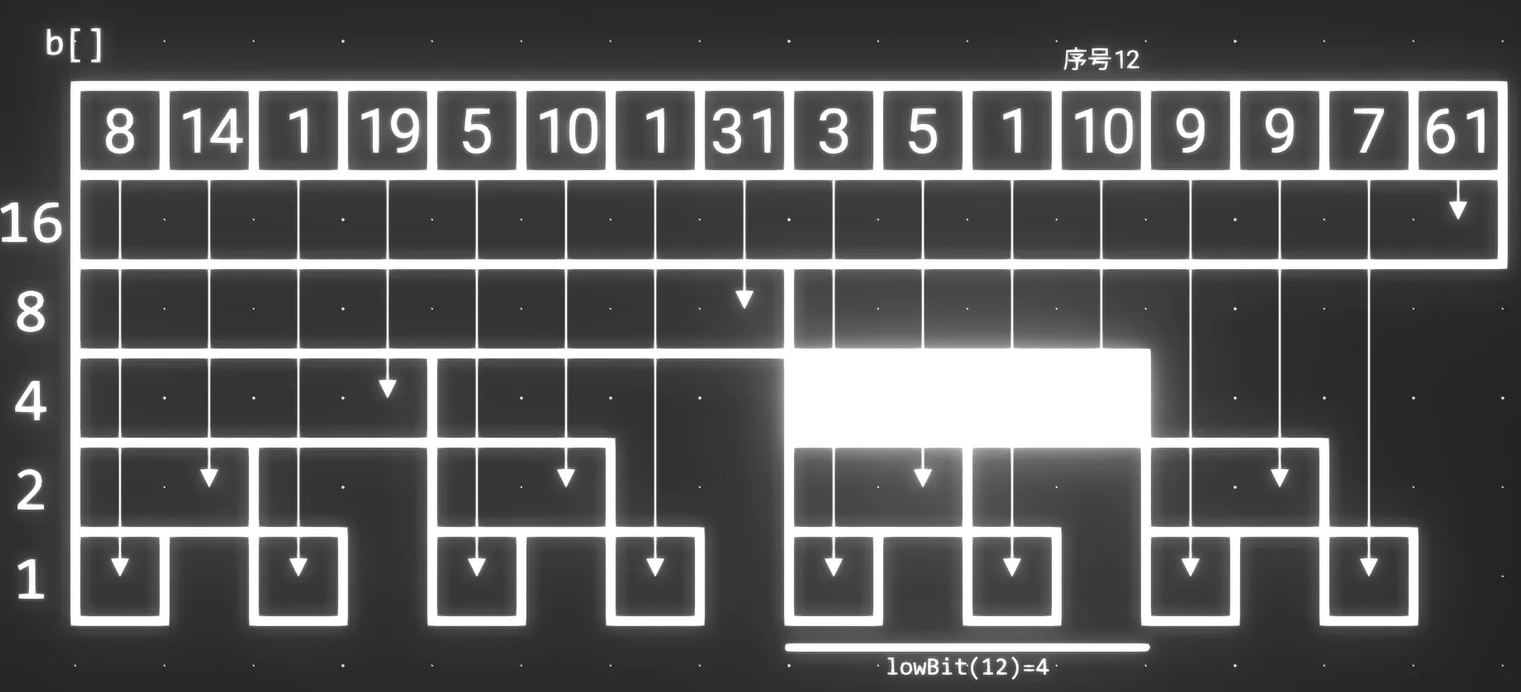
有以下两个性质:
- 序列为
i的序列正好就是长度为lowBit(i)且以i结尾的序列 - 序列
b[i]正上方的序列,正好是b[i + lowBit(i)]- 所以,我们在修改某个位置的值的时候,只需要不断加上
lowBit(i)就可以找到上方的所有序列,进行修改
- 所以,我们在修改某个位置的值的时候,只需要不断加上
inline int lowbit(int x)
{
return x &(-x);
}
void add(int p, int x) // 修改某个位置的值
{
while(p < N)
{
b[p] += x;
p += lowbit(p);
}
}
ll count(int p) // 计算前i-lowBit(i)的和加b[i]
{
ll result = 0;
while(p)
{
result += b[p];
p -= lowbit(p);
}
return result;
}树状数组求逆序对:
**离散化(Discretization)**:开一个数组
d,d[i]用来存放第i大的数在原序列的什么位置,比如原序列a={5,3,4,2,1},第一大就是5,它在a中的位是1,所以d[1]=1,同理d[2]=3,etc. 所以d数组为{1,3,2,4,5}转换后,求d中的正序对:
- 首先把1放到树状数组
t中,此时t只有一个数1,t中比1小的数没有,sum+=0 - 再把3放到树状数组
t中,此时t只有两个数1,3,比3小的数只有一个,sum+=1 - 把2放到树状数组
t中,此时t只有两个数1,2,3,比2小的数只有一个,sum+=1 - 把4放到树状数组
t中,此时t只有两个数1,2,3,4,比4小的数有三个,sum+=3 - 把5放到树状数组
t中,此时t只有两个数1,2,3,4,5,比5小的数有四个,sum+=4
- 首先把1放到树状数组
t[x]表示的是[1,x]中有几个数已经存在实现方法如下:代码
把1放进去,包含
t[1]的结点t[1]++,t[2]++、t[4]++, 由于n==5,算到t[8]的时候就已经跳出,查询[1,1-1]中比它小的数为0把3放进去, 包含
t[3]的结点t[3]++,t[4]++,然后查询[1, 3-1]中有几个数已经存在,t[2]==1,sum+=1,lowbit等于0跳出把2放进去, 包含
t[2]的结点t[2]++,t[4]++, 然后查询[1,2-1]中有几个数已经存在,t[1]==1,sum+=1,lowbit等于0跳出把4放进去,包含
t[4]的结点t[4]++,t[8]大于n跳出, 查询[1,4-1]中有几个数已经存在,t[3]==1,sum+=1,执行lowbit语句,t[2]==2,所以sum+=2把5放进去, 包含
t[5]的结点t[5]++,t[6]大于n跳出 , 查询[1,5-1]中有几个数已经存在,t[4]==4,sum+=4,执行lowbit语句,等于0跳出
2.2.2 归并排序求逆序对
我们发现一个性质:当数组分为左右两部分时,其中一个部分中的数字位置进行了交换并不会影响另外一部分与该部分之间产生的逆序对数(也就是“一左一右”的情况)。 根据归并排序流程,发现可以用归并排序排序。
则,如果右侧指针指向的数字小于左侧指针指向的数字,那么说明左侧指针所指向的数字以及该序列之后的数字均大于右侧指针所指向的数字,所以将这些数字全部记录,ans += mid - i + 1即可。
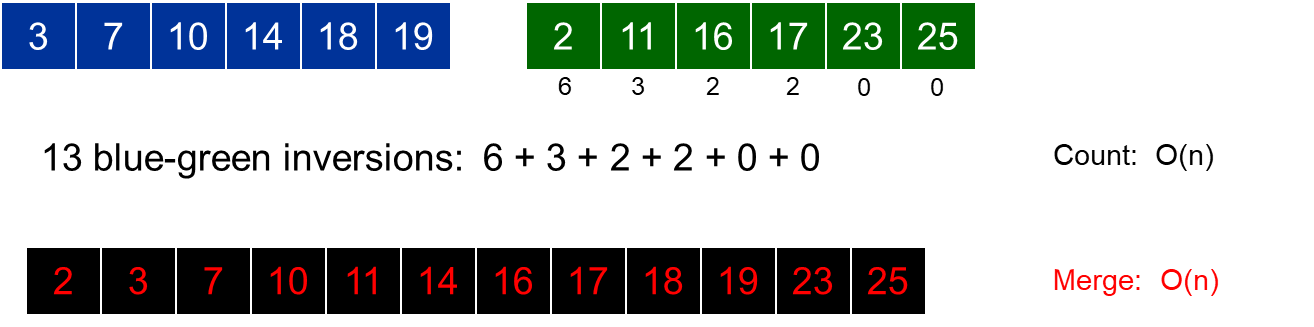
时间复杂度分析:$T(n) \leq 2T(|n / 2|)+O(n) \Rightarrow \mathrm{T}(n)=O(n \log n)$
#include<iostream>
using namespace std;
const int N = 100010;
int a[N];
long long count = 0;
void merge_sort(int q[], int l, int r)
{
if (l >= r) return;
int tmp[N];
int mid = l + r >> 1;
merge_sort(q, l, mid);
merge_sort(q, mid + 1, r);
int k = 0, i = l, j = mid + 1; // i,j指针的初始位置为两个已经排序序列的起始位置
while (i <= mid && j <= r)
if (q[i] <= q[j]) tmp[k++] = q[i++];
else {
tmp[k++] = q[j++];
count += mid - i + 1;
}
while (i <= mid) tmp[k++] = q[i++];
while (j <= r) tmp[k++] = q[j++];
for (i = l, j = 0; i <= r; i++, j++) q[i] = tmp[j];
}
int main()
{
int n;
cin >> n;
for (int i = 0; i < n; i++)
{
cin >> a[i];
}
merge_sort(a, 0, n - 1);
cout << count << endl;
return 0;
}三、减治法(Decrease&Conquer)
基本类型:
- Decrease by a constant:减去一个常量(通常是1)
- 插入排序
- 拓扑排序
- 生成排列和子集的算法
- Decrease by a constant factor:减去一个常数因子(通常是一半)
- 二分查找
- 快速幂
- multiplication à la russe
- Variable-size decrease:不定规模
- 欧几里得算法:
gcd(a,b) = gcd(b,a mod b) - 划分算法
- Nim-like games
- 欧几里得算法:
3.1 减治法的设计思想
3.1.1 计算$a^n$
减去一个常量:
- 暴力:$a^n=aaa*…*a$
- 递归:$a^n=a^{n-1}*a$
减去一个常数因子:
$a^n=(a^{n/2})^{2}$($n$为偶数)
$=(a^{(n-1)/2})^{2}*a$($n$为奇数)
$=a$($n=1$)
分治法:
$a^n=a^{\lfloor n/2 \rfloor}*a^{\lfloor n/2 \rfloor}$($n>1$)
$=a$($n=1$)
减治法只对一个子问题求解,并且不需要进行解的合并。应用减治法(例如减半法)得到的算法通常具有如下递推式:
$T(n)=\left{\begin{array}{cc}
0 & n=1 \
T(n / 2)+1 & n>1
\end{array}\right.$
通常来说,应用减治法处理问题的效率是很高的,一般是$O(log_2n)$数量级。
3.1.2 两个序列的中位数
一个长度为 $n$($n≥1$)的升序序列$S$,处在第 $n/2$ 个位置的数称为序列 $S$ 的中位数。两个序列的中位数是他们所有元素的升序序列的中位数。现有两个等长升序序列$A$ 和 $B$,试设计一个在时间和空间两方面都尽可能高效的算法,找出两个序列的中位数。
- 合并并求中位数
- 分别求中位数(减治)
分别求出两个序列的中位数,记为a和b;比较a和b,有下列三种情况:
① a = b:则a即为两个序列的中位数;
② a < b:则中位数只能出现在a和b之间,在序列$A$中舍弃a之前的元素得到序列$A_1$,在序列$B$中舍弃b之后的元素得到序列$B_1$;
③ a > b:则中位数只能出现在b和a之间,在序列$A$中舍弃a之后的元素得到序列$A_1$,在序列$B$中舍弃b之前的元素得到序列$B_1$;
在$A_1$和$B_1$中分别求出中位数,重复上述过程,直到两个序列中只有一个元素,则较小者即为所求。
对于两个给定的序列A={11, 13, 15, 17, 19}, B={2, 4, 10, 15, 20},求序列A和B的中位数的过程。
| 步骤 | 操作说明 | 序列A | 序列B |
|---|---|---|---|
| 1 | 初始序列 | {11, 13, 15, 17, 19} | {2, 4, 10, 15, 20} |
| 2 | 分别求中位数 | {11, 13, 15, 17, 19} | {2, 4, 10, 15, 20} |
| 3 | 15>10,结果在[10, 15]之间 | 舍弃15之后元素,{11,13,15} | 舍弃10之前元素,{10,15,20} |
| 4 | 分别求中位数 | {11,13,15} | {10,15,20} |
| 5 | 13<15,结果在[11, 15]之间 | 舍弃13之前元素,{13,15} | 舍弃15之后元素,{10,15} |
| 6 | 分别求中位数 | {13,15} | {10,15} |
| 7 | 10<13,结果在[10, 13]之间 | 舍弃13之后元素,{13} | 舍弃10之前元素,{15} |
| 8 | 长度为1,较小者为所求 | {13} | {15} |
我们的例子是以奇数个数序列举例的,整个算法应如下描述:
舍弃a、b中较小者所在序列之较小一半,同时舍弃较大者所在序列之较大一半,要求两次舍弃的元素个数相同。
当$S_1$长度为奇数时,左半边=右半边,直接舍弃即可;
当$S_1$长度为偶数时,左半边+1=右半边。若
a<b,舍弃a的左半边(包括中点),舍弃b的右半边(保留中点),始终保持$S_1,S_2$等长。
3.1.3 插入排序
思想:无序序列中的数插入到有序序列中。
排序$[6, 4, 1, 8, 5]$:
6 | 4 1 8 5
4 6 | 1 8 5
1 4 6 | 8 5
1 4 6 8 | 5
1 4 5 6 8
algorithm InsertionSort(A[0..n-1])
//Sorts a given array by insertion sort
//Input:An array A[0..n-1] of n orderable elements
//Output: Array A[0..n-1] sorted in nondecreasing order
for i <- 1 to n-1 do
{
v <- A[i];
j <- i-1;
while (j≥0 and A[j]>v)
{
A[j+1] <- A[j];
j <- j-1;
}
A[j+1] <- v;
}3.2 DFS
基本思路:采用递归算法。
从图中某个顶点出发,访问此顶点,然后依次从其未被访问的邻接点出发深度优先遍历图,直至所有与其有路径相同的顶点都被访问到;若此时图中尚有顶点未被访问,则另选图中一个未被访问的顶点作为起始点,重复以上过程,直至图中所有顶点都被访问到为止。
记录未被访问的节点的方法:
visited[]数组- $flag=\left{\begin{array}{cc}
0 /1 \
color(染色)
\end{array}\right.$(使用结构体) - 使用$set$,将访问过的点放入集合
DFS(G)
count :=0
未访问的顶点标记为 0
for each vertex v∈ V do
if v 的标记为 0
dfs(v) // 2
dfs(v)
count := count + 1 // 1
顶点 v 标记为 count
for each vertex w adjacent to v do
if w is marked with 0
dfs(w)注:
- 将语句1移到语句2之前,可以通过
count得到多少个连通的子图;当count == 1时为连通图;DFS可以判断是否有环;- 深度优先数(
DFN):DFS遍历到的点的序号。
复杂度分析:
空间复杂度:来自函数调用栈,最坏情况,递归深度为$O\left( \middle| V \middle| \right)$.
时间复杂度与BFS是一样的,主要取决于使用哪种数据结构来存储图:
邻接矩阵存储的图:
- 访问$\left| V \right|$个顶点需要$O\left( \middle| V \middle| \right)$的时间。查找每个顶点的邻接点都需要$O\left( \middle| V \middle| \right)$的时间,而总共有$\left| V \right|$个顶点,其时间复杂度为$O\left( \left| V \right|^{2} \right)$;
邻接表存储的图:
- 访问$\left| V \right|$个顶点需要$O\left( \middle| V \middle| \right)$的时间。查找每个顶点的邻接点都需要$O\left( \middle| E \middle| \right)$的时间,其时间复杂度为$O\left( \left| V \right| + \left| E \right| \right)$。