算法课外思考题0923(众数与求和)

💡Author：信安2002钱泽枢(ShiQuLiZhi)

🚀欢迎访问我的作业合集：https://sxhthreo.github.io/categories/%E4%BD%9C%E4%B8%9A/

1.1 问题描述

给出策略返回一系列数中的众数（majority number：出现次数不小于总数的一半），并进行性能分析。

1.2 算法思路

本题最直接的思路是从头到尾假设每个数是众数，依次遍历它在序列中出现的次数，但这样做显然时间复杂度过高，以下考虑三种算法进行求解：

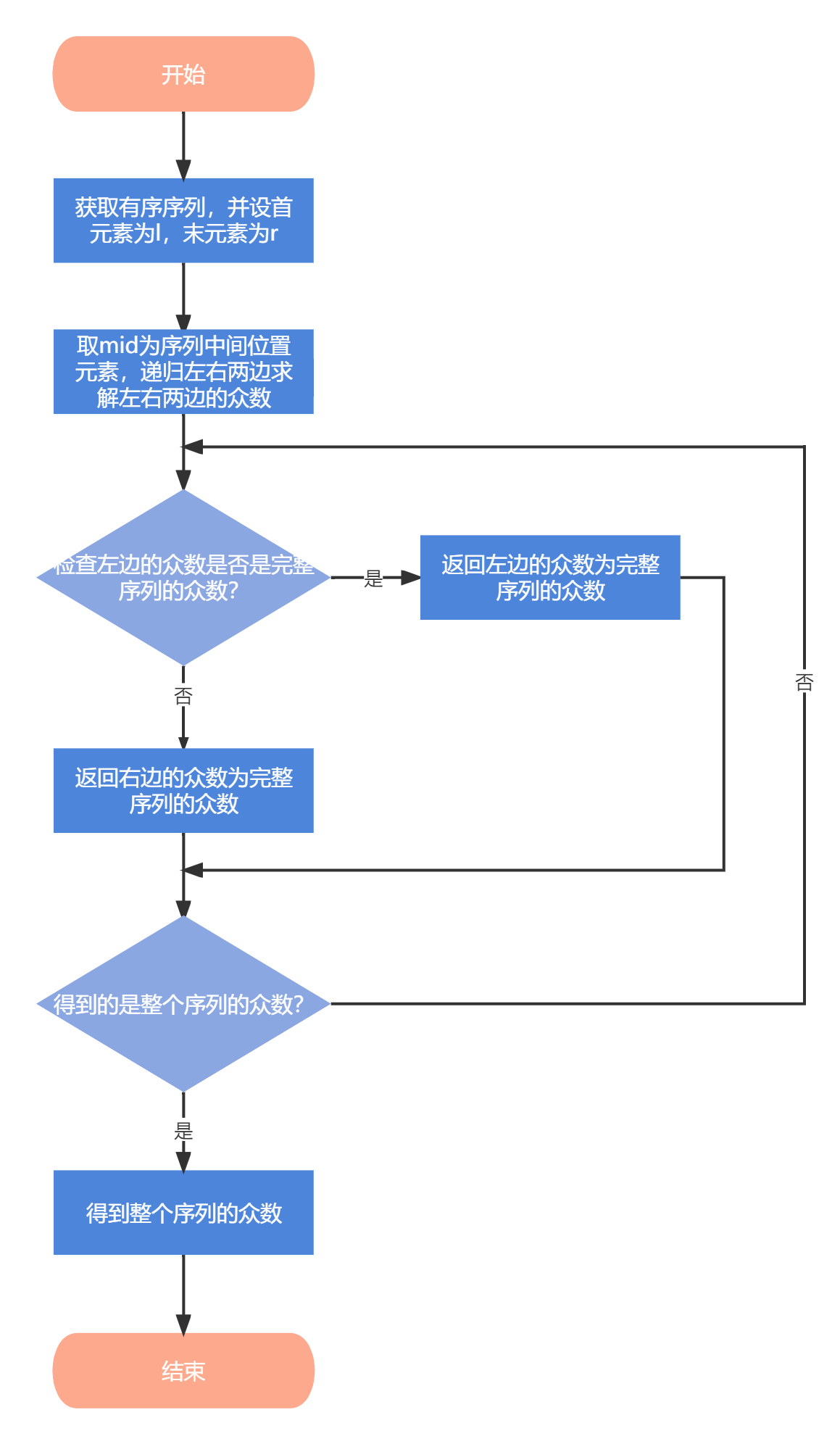
• 分治算法：依次找到左右两边序列的众数，然后通过计数判断左边序列是否仍是整个序列的众数，若是，则返回左边序列的众数为整个序列的众数，否则，右边序列的众数为整个序列的众数。采用分治思想最终能得到整个序列的众数，时间效率有所提高。

• 排序+取中间序号元素：我们将整个序列从小到大进行排序。由于众数是出现次数不小于总数的一半的元素，则排序完成后，中间序号的元素即是众数。时间代价只有排序这一个操作。

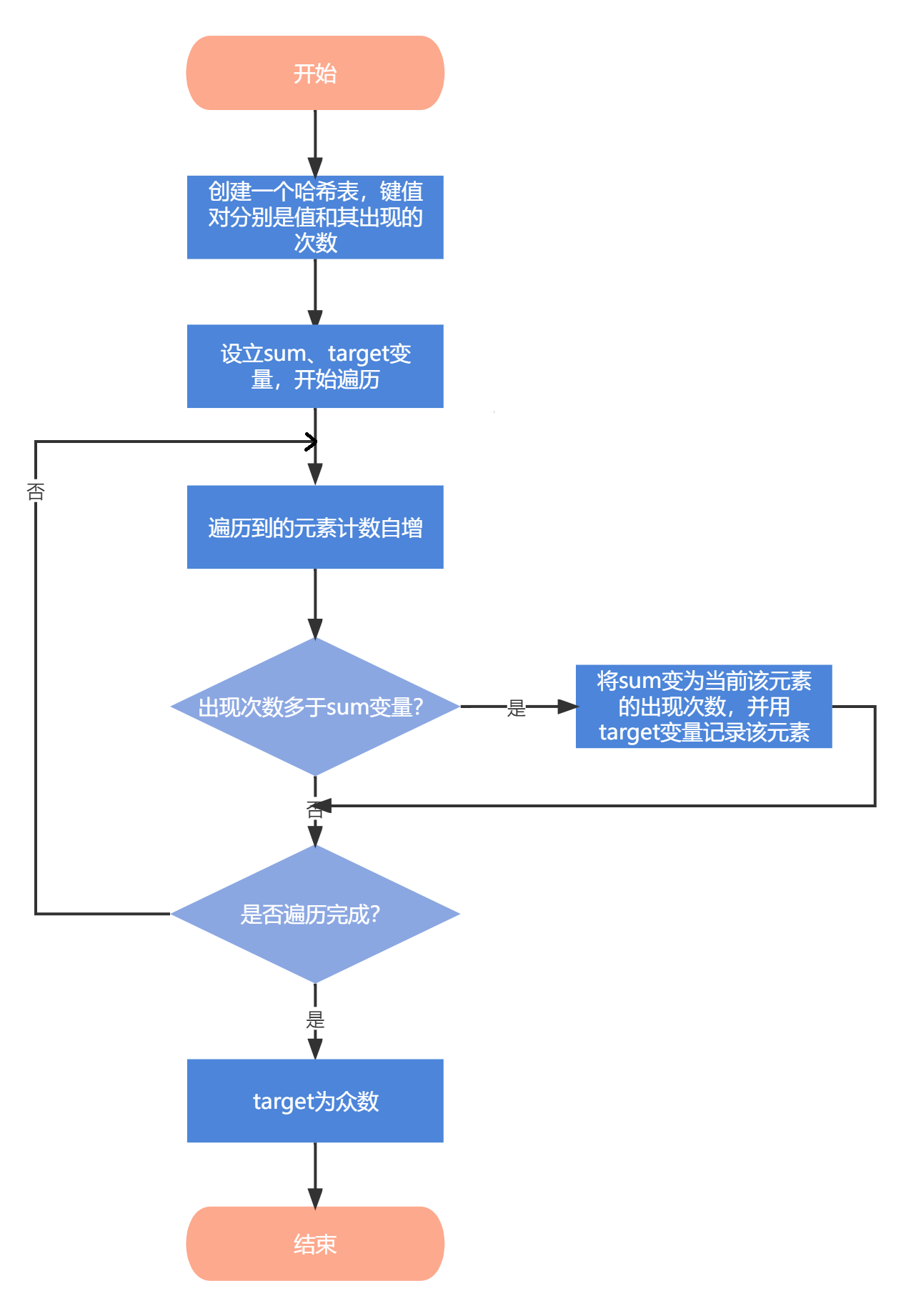
• 哈希：创建一个哈希表，键值对分别是值和其出现的次数。遍历序列过程中，每次将对应的值出现的次数自增，最后对哈希表进行遍历，找到出现次数大于等于总数一半的元素，只需两次遍历就能求得答案。

  实际上，还可以只遍历一次，即当遍历时，设立一个sum变量，每次发现出现次数多于sum变量值时，将sum变为当前该元素的出现次数，并用target变量记录该元素。扫描完成后，target即为众数。这种算法不仅能找出序列中出现次数不小于总数的一半的元素，对找出序列中出现次数最多的元素同样适用。

1.3 算法图解

• 分治算法：

• 排序+取中间序号元素思路较简单，算法示意图略
• 哈希：

1.4 代码设计

方法1：分治算法

int Count(int q[], int element, int l, int r)
{
	int count = 0;
	for (int i = l; i <= r; i++)
	{
		if (q[i] == element)
		{
			count++;
		}
	}
	return count;
}

int Modal_number(int q[], int l, int r)
{
	if (l == r)
	{
		return q[l];		//若数组中仅有一个元素
	}
	int mid = l + r >> 1;
	int l_element = Modal_number(q, l, mid);
	int r_element = Modal_number(q, mid + 1, r);

	if (Count(q, l_element, l, r) > (r - l + 1) / 2)	//检查左边的众数是否是完整序列的众数
	{
		return l_element;
	}
	else
	{
		return r_element;
	}
}

方法2：排序+取中间序号元素

void merge_sort(int q[], int l, int r)
{
    if (l >= r) return;

    int mid = l + r >> 1, tmp[Inf];
    merge_sort(q, l, mid);
    merge_sort(q, mid + 1, r);

    int k = 0, i = l, j = mid + 1;
    while (i <= mid && j <= r)
        if (q[i] <= q[j]) tmp[k++] = q[i++];
        else tmp[k++] = q[j++];

    while (i <= mid) tmp[k++] = q[i++];
    while (j <= r) tmp[k++] = q[j++];

    for (i = l, j = 0; i <= r; i ++, j ++ ) q[i] = tmp[j];
}

int Modal_number(int q[],int n)     //n表示数组长度
{
    merge_sort(q, 0, n - 1);
    return q[n / 2];                //中间位置的一定是众数
}

方法3：哈希

int Modal_number(int q[], int n)
{
    unordered_map<int, int> counts;
    for (int i = 0; i < n; i++)         //n为数组长度
    {
        ++counts[q[i]];
    }
    for (auto x : counts)
    {
        if (x.second >= n / 2)
        {
            return x.first;
        }
    }
}

或直接一次扫描优化，即：

int Modal_number(int q[],int n)
{
    unordered_map<int, int> counts;
    int target, sum = 0;
    for (int i = 0; i < n; i++)         //n为数组长度
    {
        if (++counts[q[i]] > sum)
        {
            target = q[i];
            sum = counts[q[i]];
        }
    }
    return target;
}

1.5 测试结果

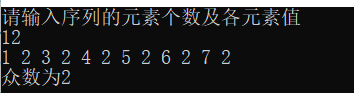
多次测试，算法运行结果均正确，符合题意。

1.6 总结与讨论

讨论三种算法的时间复杂度：

• 分治算法：$T(n)=2T(n/2)+O(n)$，由主定理法可知，$T(n)=O(nlogn)$；
• 排序+取中间序号元素：该算法的时间复杂度依赖于排序算法的时间复杂度，取中间序号元素可以在$O(1)$时间内完成。我们采用归并排序、快速排序等排序算法，则$T(n)=O(nlogn)$；
• 哈希：算法只需遍历序列即可得到众数，则$T(n)=O(n)$。

由此可见，分治算法和排序后取中间序号元素算法时间复杂度都在$O(nlogn)$时间内完成；而使用哈希表获取众数时，代码简洁，时间复杂度仅为$O(n)$，且适用性广泛，可用于获取序列中出现次数最多的数。

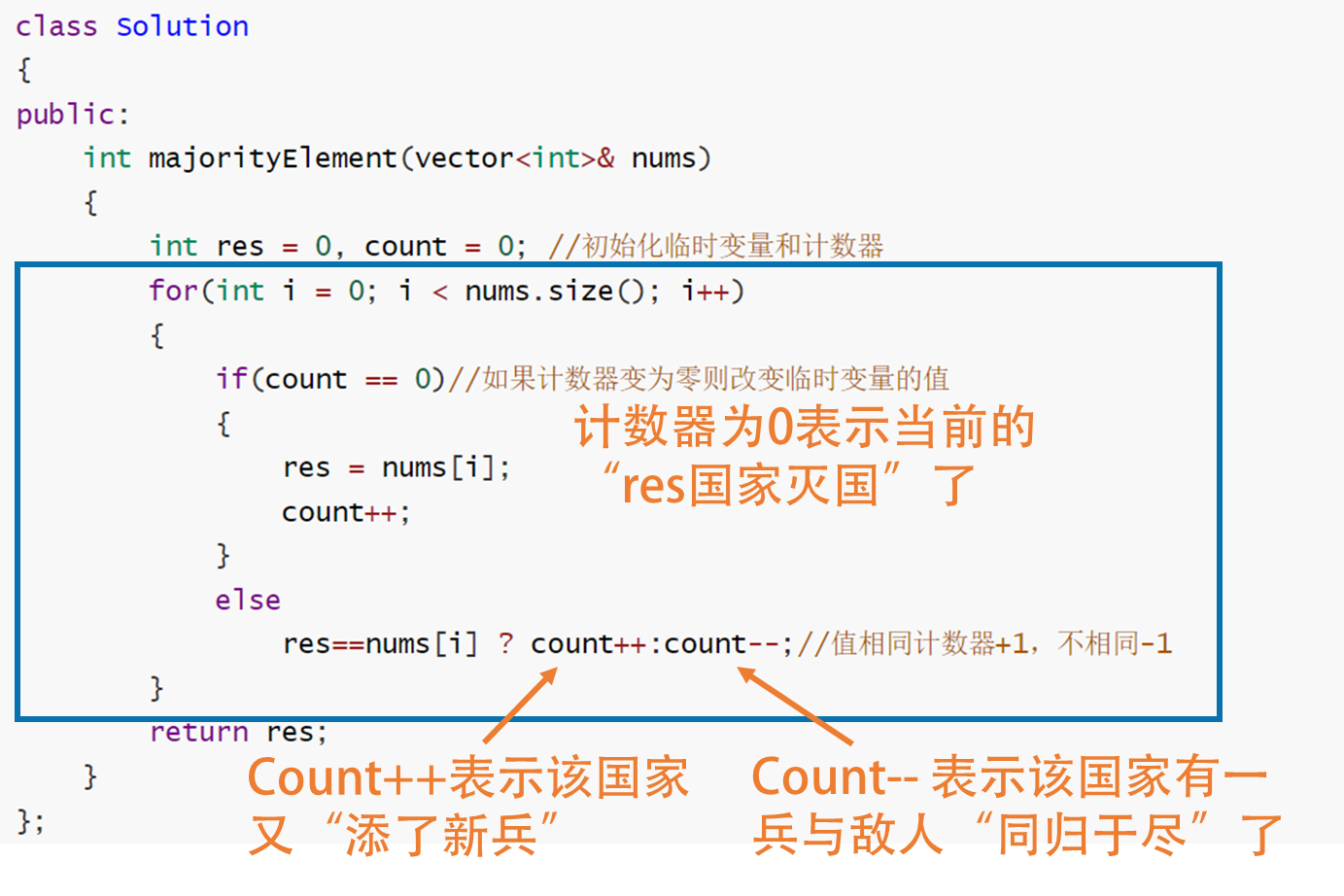
补充：摩尔投票法

摩尔投票的前提是一定存在众数，如果不存在众数算法得出来的不是真实答案。

2.1 问题描述

给定一系列的实数集合S以及实数x，给出策略判定S中是否有两个实数的和等于x，并做算法分析。

2.2 算法思路

以下考虑三种算法进行求解：

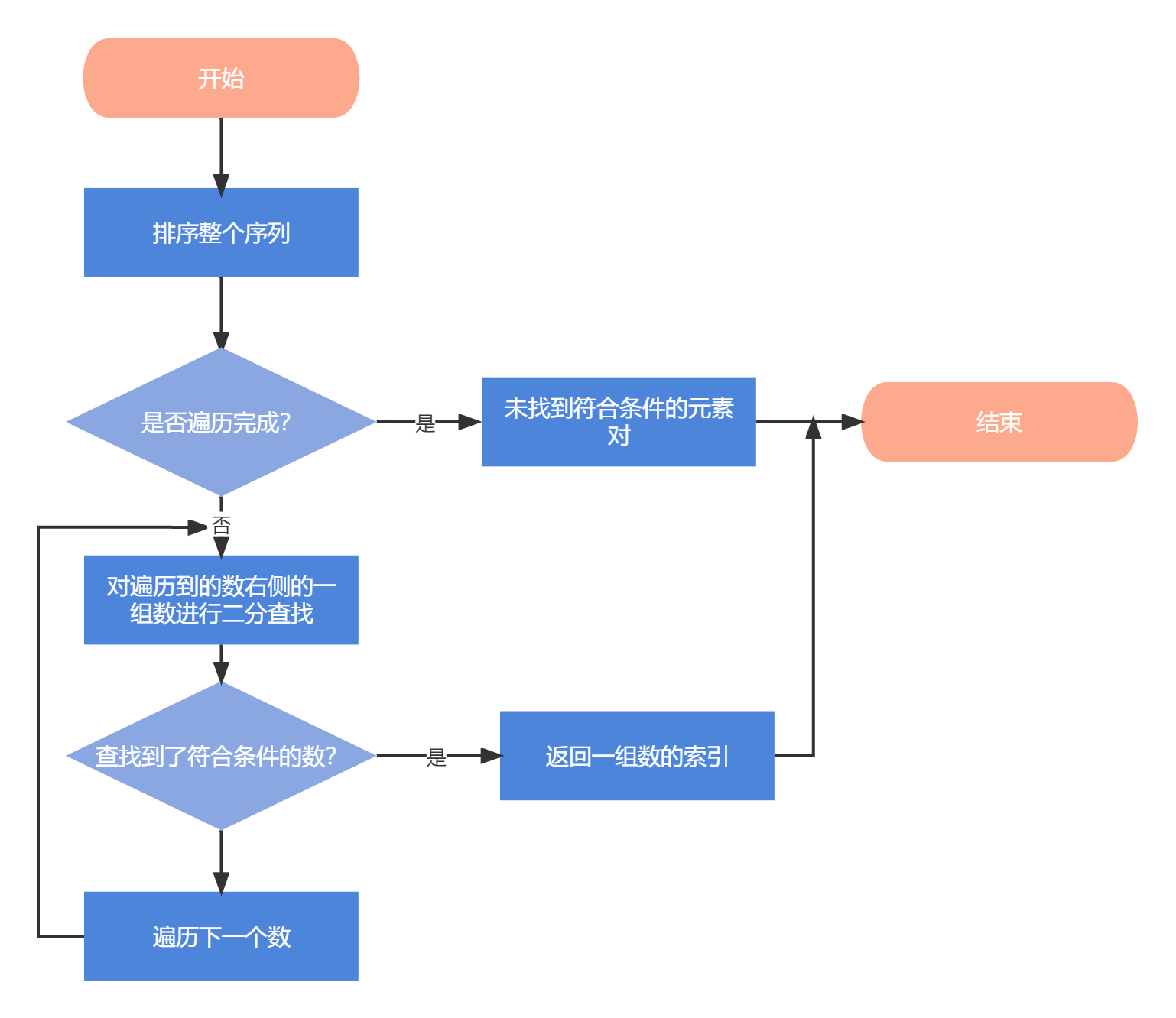
• 排序+二分查找：本题中，我们可以先排序，并遍历排序好的集合。将遍历到的数作为第一个数，并在第一个数的右侧通过二分查找找到第二个数，时间性能依赖于排序和二分查找的时间复杂度。

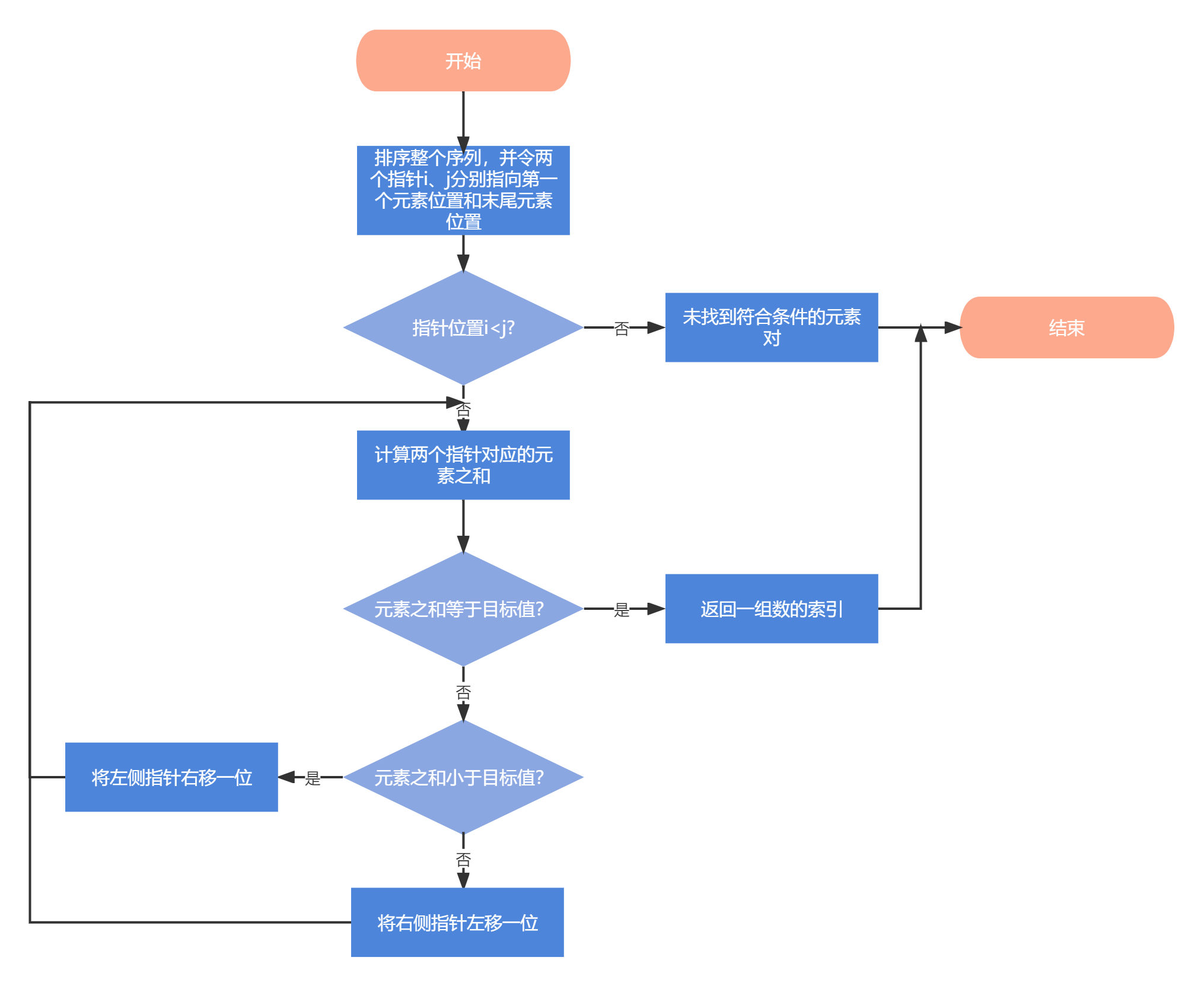
• 排序+双指针算法：当排序好序列后，我们还可以使用双指针算法遍历排序好的集合，以此缩小范围，提高时间性能。初始时两个指针分别指向第一个元素位置和最后一个元素的位置。每次计算两个指针指向的两个元素之和，并和目标值比较。如果两个元素之和等于目标值，则发现了一组解。如果两个元素之和小于目标值，则将左侧指针右移一位；如果两个元素之和大于目标值，则将右侧指针左移一位。

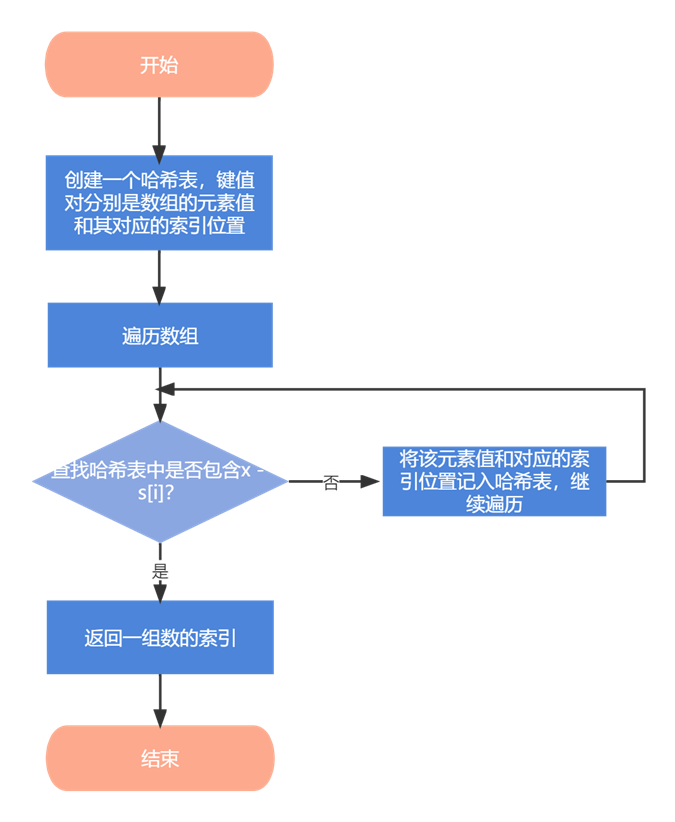
• 哈希：我们可以使用哈希求解此问题，且不需排序的开销。我们创建一个哈希表，键值对分别是数组的元素值和其对应的索引位置。遍历数组时，我们查找哈希表中是否包含x - s[i]，若包含，则为一组解，并返回，否则将该元素值和对应的索引位置记入哈希表。算法时间性能进一步提高。

注：双指针算法不会把解过滤掉。设下标为i和j的位置是解。

如果左指针先到达下标i的位置，此时右指针还在下标j的右侧，$sum>target$，因此一定是右指针左移，左指针不可能移到i的右侧。

如果右指针先到达下标j的位置，此时左指针还在下标i的左侧，$sum<target$，因此一定是左指针右移，右指针不可能移到j的左侧。

由此可见，在整个移动过程中，左指针不可能移到i的右侧，右指针不可能移到j的左侧，因此不会把可能的解过滤掉。

2.3 算法图解

• 方法1：排序+二分查找

• 方法2：排序+双指针算法

• 方法3：哈希

2.4 代码设计

注：以下方法的代码设计中序列元素默认为整型，使用int型变量，在实际问题的求解中可设为Elemtype型或double型变量(规定为实数情况下)。

方法1：排序+二分查找

void merge_sort(int s[], int l, int r)
{
	if (l >= r) return;

	int mid = l + r >> 1, tmp[Inf];
	merge_sort(s, l, mid);
	merge_sort(s, mid + 1, r);

	int k = 0, i = l, j = mid + 1;
	while (i <= mid && j <= r)
		if (s[i] <= s[j]) tmp[k++] = s[i++];
		else tmp[k++] = s[j++];

	while (i <= mid) tmp[k++] = s[i++];
	while (j <= r) tmp[k++] = s[j++];

	for (i = l, j = 0; i <= r; i++, j++) s[i] = tmp[j];
}

int Binary_Search(int s[], int n, int key)		//二分查找
{
	int low = 0, high = n - 1;
	while (low <= high)
	{
		int mid = (low + high) / 2;				//取中间位置
		if (s[mid] == key)
		{
			return mid;							//查找成功则返回所在位置
		}
		else if (s[mid] > key)
		{
			high = mid - 1;						//从前半部分继续查找
		}
		else
		{
			low = mid + 1;						//从后半部分继续查找
		}
	}
	return -1;
}

pair<int, int> GetSum(int s[], int n, int target)
{
	merge_sort(s, 0, n - 1);
	for (int i = 0; i < n; i++)
	{
		int index = Binary_Search(s, n, target - s[i]);
		if (index != -1)		//查找到了符合条件的数
		{
			return { i,index };
		}
	}
	return { -1,-1 };
}

方法2：排序+双指针算法

归并排序算法的函数同方法1。

pair<int, int> GetSum(int s[], int n, int target)
{
	int l = 0, r = n - 1;
	merge_sort(s, 0, n - 1);
	while (l < r)
	{
		int sum = s[l] + s[r];
		if (sum == target)
		{
			return { l,r };
		}
		else if (sum > target)
		{
			r--;
		}
		else 
		{
			l++;
		}
	}
	return { -1,-1 };
}

方法3：哈希

pair<int, int> GetSum(int s[], int n, int target)
{
	int l = 0, r = n - 1;
	unordered_map<int, int> hashmap;
	for (int i = n - 1; i >= 0; i--)
	{
		if (hashmap.find(target - s[i]) != hashmap.end())		// 若未找到将返回end()
		{
			return { i,hashmap[target - s[i]] };
		}
		hashmap.insert({ s[i],i });
	}
	return { -1,-1 };
}

2.5 测试结果

多次测试，算法运行结果均正确，符合题意。

2.6 总结与讨论

讨论三种算法的时间复杂度：

• 排序+二分查找：算法时间复杂度依赖于排序和二分查找的时间复杂度。排序算法时间复杂度在$O(nlogn)$时间内完成；遍历序列并进行二分查找，对单个序列的二分查找的时间复杂度是$O(logn)$，对所有元素遍历并进行二分查找最坏的时间复杂度是$O(nlogn)$，则算法的时间复杂度是$O(nlogn)$；
• 排序+双指针算法：算法时间复杂度依赖于排序和双指针算法的时间复杂度。排序算法时间复杂度在$O(nlogn)$时间内完成；双指针算法仅需遍历一次序列即可，时间复杂度是$O(n)$的，则算法的时间复杂度是$O(nlogn)$；
• 哈希：算法只需遍历序列即可得到，则$T(n)=O(n)$。

由此可见，前两种算法的时间复杂度都在$O(nlogn)$时间内完成。其中，排序后通过具有分治思想的二分查找算法来求解问题时，时间复杂度较双指针算法略高；而使用哈希表获取加和为$x$的一组数时，代码简洁，无需事先排序，时间复杂度仅为$O(n)$，具有较高的时间性能。

附：源代码

算法题1：

方法1：

#include<iostream>
using namespace std;
const int Inf = 20;

int Count(int q[], int element, int l, int r)
{
	int count = 0;
	for (int i = l; i <= r; i++)
	{
		if (q[i] == element)
		{
			count++;
		}
	}
	return count;
}

int Modal_number(int q[], int l, int r)
{
	if (l == r)
	{
		return q[l];		//若数组中仅有一个元素
	}
	int mid = l + r >> 1;
	int l_element = Modal_number(q, l, mid);
	int r_element = Modal_number(q, mid + 1, r);

	if (Count(q, l_element, l, r) > (r - l + 1) / 2)	//检查左边的众数是否是所有序列的众数
	{
		return l_element;
	}
	else
	{
		return r_element;
	}
}

int main()
{
	int n, q[Inf];
	cout << "请输入序列的元素个数及各元素值" << endl;
	cin >> n;
	for (int i = 0; i < n; i++)
	{
		cin >> q[i];
	}
	cout << "众数为" << Modal_number(q, 0, n-1) << endl;
	return 0;
}

方法2：

#include<iostream>
using namespace std;
const int Inf = 20;

void merge_sort(int q[], int l, int r)
{
    if (l >= r) return;

    int mid = l + r >> 1, tmp[Inf];
    merge_sort(q, l, mid);
    merge_sort(q, mid + 1, r);

    int k = 0, i = l, j = mid + 1;
    while (i <= mid && j <= r)
        if (q[i] <= q[j]) tmp[k++] = q[i++];
        else tmp[k++] = q[j++];

    while (i <= mid) tmp[k++] = q[i++];
    while (j <= r) tmp[k++] = q[j++];

    for (i = l, j = 0; i <= r; i ++, j ++ ) q[i] = tmp[j];
}

int Modal_number(int q[],int n)     //n表示数组长度
{
    merge_sort(q, 0, n - 1);
    return q[n / 2];                //中间位置的一定是众数
}

int main()
{
    int n, q[Inf];
    cout << "请输入序列的元素个数及各元素值" << endl;
    cin >> n;
    for (int i = 0; i < n; i++)
    {
        cin >> q[i];
    }
    cout << "众数为" << Modal_number(q,n) << endl;
    return 0;
}

方法3：

#include<iostream>
#include<unordered_map>
using namespace std;
const int Inf = 20;

int Modal_number(int q[],int n)
{
    unordered_map<int, int> counts;
    int target = 0, sum = 0;
    for (int i = 0; i < n; i++)         //n为数组长度
    {
        if (++counts[q[i]] > sum)
        {
            target = q[i];
            sum = counts[q[i]];
        }
    }
    return target;
}

int main()
{
    int n, q[Inf];
    cout << "请输入序列的元素个数及各元素值" << endl;
    cin >> n;
    for (int i = 0; i < n; i++)
    {
        cin >> q[i];
    }
    cout << "众数为" << Modal_number(q,n) << endl;
    return 0;
}

算法题2：

方法1：

#include<iostream>
#include<utility>
using namespace std;
const int Inf = 20;

void merge_sort(int s[], int l, int r)
{
	if (l >= r) return;

	int mid = l + r >> 1, tmp[Inf];
	merge_sort(s, l, mid);
	merge_sort(s, mid + 1, r);

	int k = 0, i = l, j = mid + 1;
	while (i <= mid && j <= r)
		if (s[i] <= s[j]) tmp[k++] = s[i++];
		else tmp[k++] = s[j++];

	while (i <= mid) tmp[k++] = s[i++];
	while (j <= r) tmp[k++] = s[j++];

	for (i = l, j = 0; i <= r; i++, j++) s[i] = tmp[j];
}

int Binary_Search(int s[], int n, int key)		//二分查找
{
	int low = 0, high = n - 1;
	while (low <= high)
	{
		int mid = (low + high) / 2;				//取中间位置
		if (s[mid] == key)
		{
			return mid;							//查找成功则返回所在位置
		}
		else if (s[mid] > key)
		{
			high = mid - 1;						//从前半部分继续查找
		}
		else
		{
			low = mid + 1;						//从后半部分继续查找
		}
	}
	return -1;
}

pair<int, int> GetSum(int s[], int n, int target)
{
	merge_sort(s, 0, n - 1);
	for (int i = 0; i < n; i++)
	{
		int index = Binary_Search(s, n, target - s[i]);
		if (index != -1)		//查找到了符合条件的数
		{
			return { i,index };
		}
	}
	return { -1,-1 };
}

int main()
{
	int n, target, s[Inf];
	pair<int, int> q;
	cout << "请输入序列的元素个数及各元素值" << endl;
	cin >> n;
	for (int i = 0; i < n; i++)
	{
		cin >> s[i];
	}
	cout << "请输入给定的实数" << endl;
	cin >> target;
	q = GetSum(s, n, target);
	if (q.first == -1)
	{
		cout << "未找到符合题意的一组解" << endl;
	}
	else
	{
		cout << "解为" << s[q.first] << " " << s[q.second] << endl;
	}
	return 0;
}

方法2：

#include<iostream>
#include<utility>
using namespace std;
const int Inf = 20;

void merge_sort(int s[], int l, int r)
{
	if (l >= r) return;

	int mid = l + r >> 1, tmp[Inf];
	merge_sort(s, l, mid);
	merge_sort(s, mid + 1, r);

	int k = 0, i = l, j = mid + 1;
	while (i <= mid && j <= r)
		if (s[i] <= s[j]) tmp[k++] = s[i++];
		else tmp[k++] = s[j++];

	while (i <= mid) tmp[k++] = s[i++];
	while (j <= r) tmp[k++] = s[j++];

	for (i = l, j = 0; i <= r; i++, j++) s[i] = tmp[j];
}


pair<int, int> GetSum(int s[], int n, int target)
{
	int l = 0, r = n - 1;
	merge_sort(s, 0, n - 1);
	while (l < r)
	{
		int sum = s[l] + s[r];
		if (sum == target)
		{
			return { l,r };
		}
		else if (sum > target)
		{
			r--;
		}
		else 
		{
			l++;
		}
	}
	return { -1,-1 };
}

int main()
{
	int n, target, s[Inf];
	pair<int, int> q;
	cout << "请输入序列的元素个数及各元素值" << endl;
	cin >> n;
	for (int i = 0; i < n; i++)
	{
		cin >> s[i];
	}
	cout << "请输入给定的实数" << endl;
	cin >> target;
	q = GetSum(s, n, target);
	if (q.first == -1)
	{
		cout << "未找到符合题意的一组解" << endl;
	}
	else
	{
		cout << "解为" << s[q.first] << " " << s[q.second] << endl;
	}
	return 0;
}

方法3：

#include<iostream>
#include<utility>
#include<unordered_map>
using namespace std;
const int Inf = 20;

pair<int, int> GetSum(int s[], int n, int target)
{
	int l = 0, r = n - 1;
	unordered_map<int, int> hashmap;
	for (int i = n - 1; i >= 0; i--)
	{
		if (hashmap.find(target - s[i]) != hashmap.end())		// 若未找到将返回end()
		{
			return { i,hashmap[target - s[i]] };
		}
		hashmap.insert({ s[i],i });
	}
	return { -1,-1 };
}

int main()
{
	int n, target, s[Inf];
	pair<int, int> q;
	cout << "请输入序列的元素个数及各元素值" << endl;
	cin >> n;
	for (int i = 0; i < n; i++)
	{
		cin >> s[i];
	}
	cout << "请输入给定的实数" << endl;
	cin >> target;
	q = GetSum(s, n, target);
	if (q.first == -1)
	{
		cout << "未找到符合题意的一组解" << endl;
	}
	else
	{
		cout << "解为" << s[q.first] << " " << s[q.second] << endl;
	}
	return 0;
}