算法课外思考题0930(Top k问题与波谷)

💡Author：信安2002钱泽枢(ShiQuLiZhi)

🚀欢迎访问我的作业合集：https://sxhthreo.github.io/categories/%E4%BD%9C%E4%B8%9A/

一、Top k问题

给出不同策略求解Top k 问题，并进行分析。

1.1 冒泡排序

1.1.1 算法思路

这个问题最直接也是最笨的思路就是直接排序，排序完取出最大的k个即可，时间复杂度取决于排序算法的时间性能，当采用快速排序或归并排序时，时间复杂度为$O(nlogn)$。我们使用冒泡排序，并进行优化，每次冒泡都是找到序列中第i大的数(i为冒泡的次数)，当i = k时，即可找到序列中Top k的数。

1.1.2 代码设计

void bubblesort(int a[], int k, int n)
{
	for (int i = 0; i < k; i++)
	{
		for (int j = n - 2; j >= i; j--)		//j控制每轮需要比较的次数 
		{
			if (a[j + 1] > a[j])				//不满足逆序要求，交换顺序 
			{
				int temp = a[j];
				a[j] = a[j + 1];
				a[j + 1] = temp;
			}
		}
	}
}

1.1.3 算法复杂度分析

冒泡排序中，我们每次将序列中第i大冒泡到序列前面，直到n = k，则需要遍历k次序列，时间复杂度为$O(k * n)$。

1.2 堆排序

1.2.1 算法思路

我们先用前k个元素生成一个小顶堆，然后从序列第k + 1个元素开始遍历，如果遍历到的元素大于堆顶(堆顶为堆中的最小元素)，则调整堆，直到遍历完成，得到当前序列的Top k。

1.2.2 算法图解

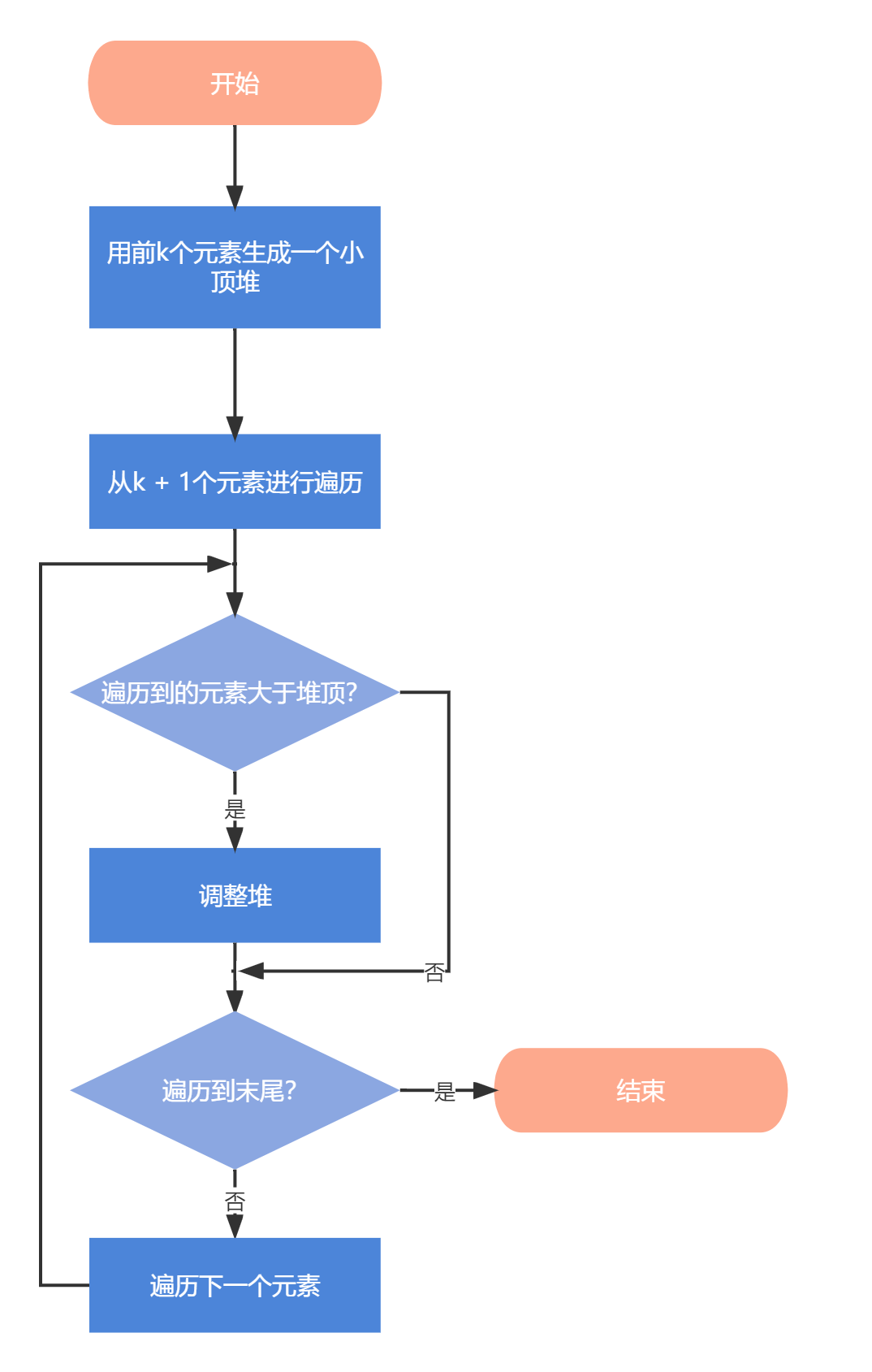
1.2.3 代码设计

void down(int u, int h[], int k)
{
    int t = u;	//t为点、左孩子、右孩子三个点中最小的一个点
    if (u * 2 <= k && h[u * 2] < h[t]) t = u * 2;
    if (u * 2 + 1 <= k && h[u * 2 + 1] < h[t]) t = u * 2 + 1;
    if (u != t)		//根节点不是最小的
    {
        //与最小的点交换
        swap(h[u], h[t]);
        down(t, h, k);	    //递归处理
    }
}

void up(int u, int h[], int k)
{
    while (u / 2 && h[u] < h[u / 2])
    {
        swap(h[u / 2], h[u]);
        u >>= 1;		    //u /= 2换上去
    }
}

void HeapSort(int h[], int k,int n)
{
    for (int i = k / 2; i; i--) down(i, h, k);	    //O(n)的时间复杂度将前k个元素建堆

    for (int i = k + 1; i <= n; i++)
    {
        if (h[i] > h[1])
        {
            h[1] = h[i];
            down(1, h, k);
        }
    }
}

1.2.4 算法复杂度分析

堆排序的时间复杂度取决于建堆和堆排序的时间。初始化建堆的时间复杂度为$O(n)$(这里的n = k)，排序重建堆的时间复杂度为$O(nlogn)$，所以总的时间复杂度为$O(n)+O(nlogn)=O(nlogn)$。

1.3 减治法

1.3.1 算法思路

我们先找到第k大的数，借用“快速排序”的思想，对整个序列进行划分(取序列第一个元素作为枢轴，也可采用随机法、三数取中法等方法)，并返回划分后的位置，若等于k则得到答案；若大于k，则说明该元素左边的元素都大于k，递归求解该位置前面序列第k大的元素即可；若小于k，则递归求解该位置后面序列第k - count(count为该序列中[l,j]的元素数量，其中j为划分后的元素位置)大的元素即可。由此，每次仅需求解大问题的一个子问题，最后即可得到第k大的数，则包括它左边的元素即为Top k的数。

1.3.2 算法图解

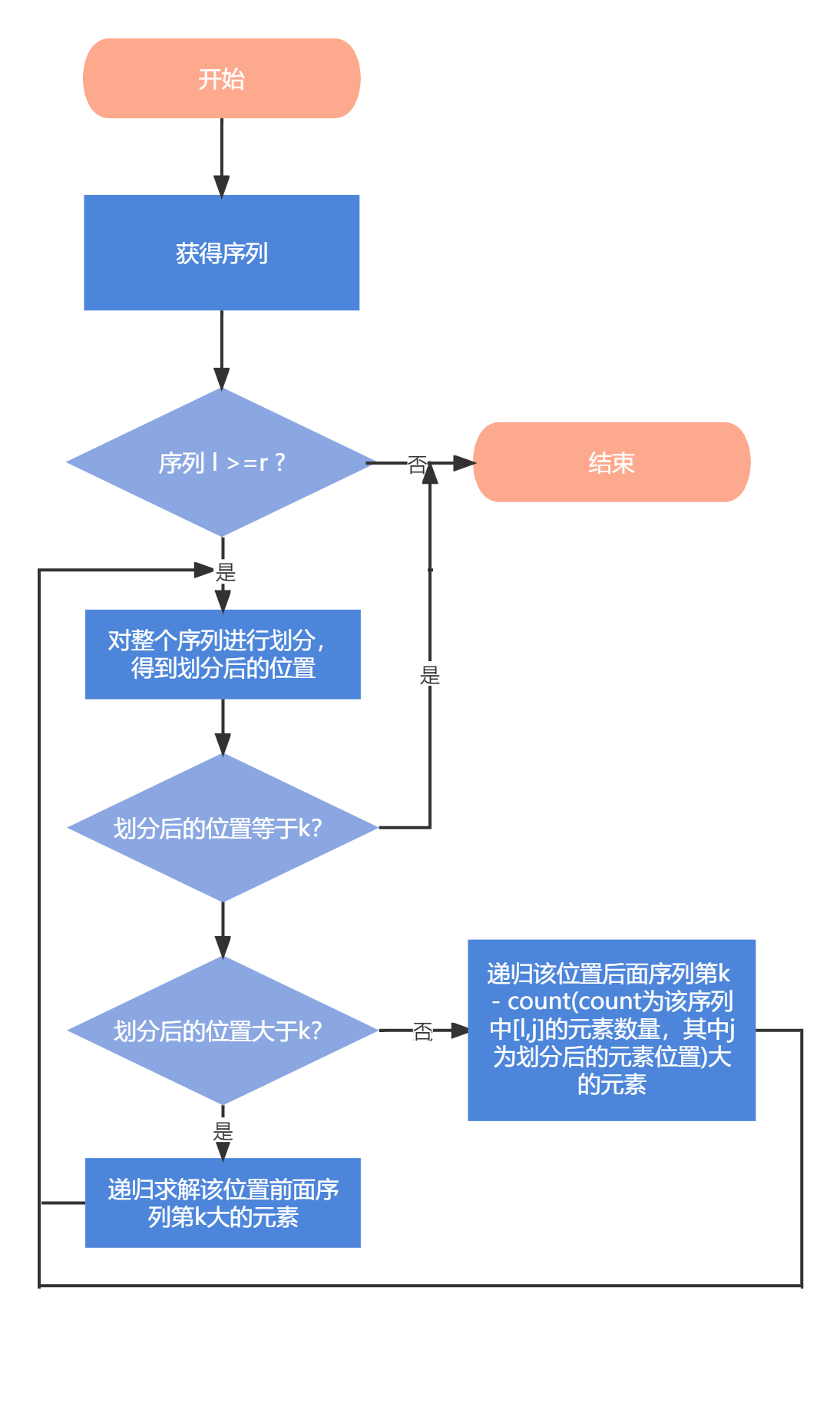
1.3.3 代码设计

int Partition(int a[], int l, int r)
{
	int pivot = a[l];						// 取序列第一个元素为pivot
	int i = l - 1, j = r + 1;
	do
	{
		do { i++; } while (a[i] > pivot);
		do { j--; } while (a[j] < pivot);
		if (i < j)  swap(a[i], a[j]);
	} while (i < j);

	return j;
}

void Top_k(int a[], int l, int r, int k)
{
	if (l >= r) return;
	int j = Partition(a, l, r);
	int count = j - l + 1;					// [l,j]区间共有多少数
	if (count == k)
	{
		return;
	}
	else if(count > k)
	{
		Top_k(a, l, j, k);					//前半部分第k大的数
	}
	else
	{
		Top_k(a, j + 1, r, k - count);		//后半部分第k - count大的数
	}
}

Partition函数还可写成“枢轴归位”的形式，但需注意边界条件：

int Partition(int a[], int l, int r)
{
	int pivot = a[l];						// 取序列第一个元素为pivot
	int i = l, j = r + 1;
	do
	{
		do { i++; } while (a[i] > pivot && i < r);
		do { j--; } while (a[j] < pivot);
		if (i < j)  swap(a[i], a[j]);
	} while (i < j);

	a[l] = a[j];  a[j] = pivot;

	return j;
}

1.3.4 算法复杂度分析

在减治法中，划分算法的时间复杂度为$O(i)$($i$为序列的长度)，则我们有$T(n)=\frac{1}{n} \sum_{i=0}^{n-1}(i+T(i))$，令$T(n + 1)=\frac{1}{n + 1} \sum_{i=0}^{n}(i+T(i))$，得到$(n+1)T(n+1)-nT(n)=T(n)+n+1$，替代法可知$T(n)=n$。

1.4 测试结果

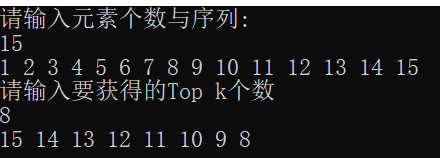
多次测试，算法运行结果均正确，符合题意。

1.5 总结与讨论

我们对比以上三种算法的时间复杂度：

• 冒泡排序：$T(n)=O(k * n)$
• 堆排序：$T(n)=O(nlogn)$
• 减治法：$T(n)=n$

通过对以上三种算法时间复杂度的比较，使用减治法的时间性能是最优的。

在大规模数据处理中，我们经常会遇到Top k问题。比如，在搜索引擎中，统计搜索最热门的10个查询词；在歌曲库中统计下载率最高的前10首歌等等。可以看到，选择恰当的数据结构来求解实际的工程问题是很关键的。

我在代码设计时遇到以下问题：

• 划分算法的边界条件未判断正确；
• 当划分后的位置小于k时，递归后面的元素Top_k(a, j + 1, r, k - count);开始误写为k - j(j为划分后的位置)，这是有问题的，应为k - count(count为该序列中[l,j]的元素数量)。

二、最大波谷问题

对于一个由n个数形成的序列，我们说其中l-序列（长度为l的子序列）的最小值为波谷，请给出策略求序列中的l-序列的波谷的最大值，即最大波谷，并进行分析。

2.1 滑动窗口法

2.1.1 算法思路

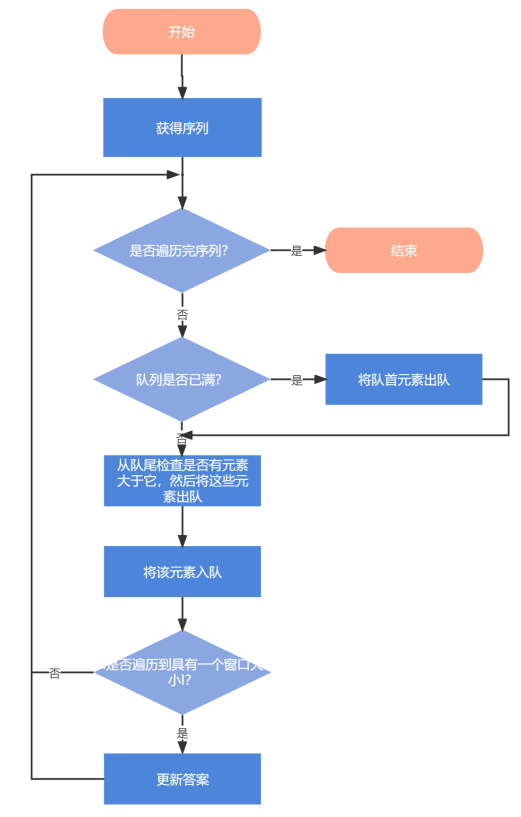
类比《计算机网络》课程中的TCP滑动窗口机制，我们固定滑动的窗口大小为l，并采用队列对窗口数据元素进行存储与比较。队列的动态变化主要涉及两种操作：

• 队首元素出序列：当队列已满时，需要将队首元素出队；
• 队尾元素入队：当新元素需要入队时，首先从队尾开始检查是否有元素大于它，这些元素都应出队；然后将该元素入队；

当i遍历到具有一个窗口大小l时，开始更新答案。由于这里涉及到从队首、队尾出队和从队尾入队的操作，我们考虑采用**双端队列deque**这一数据结构进行设计。

2.1.2 算法图解

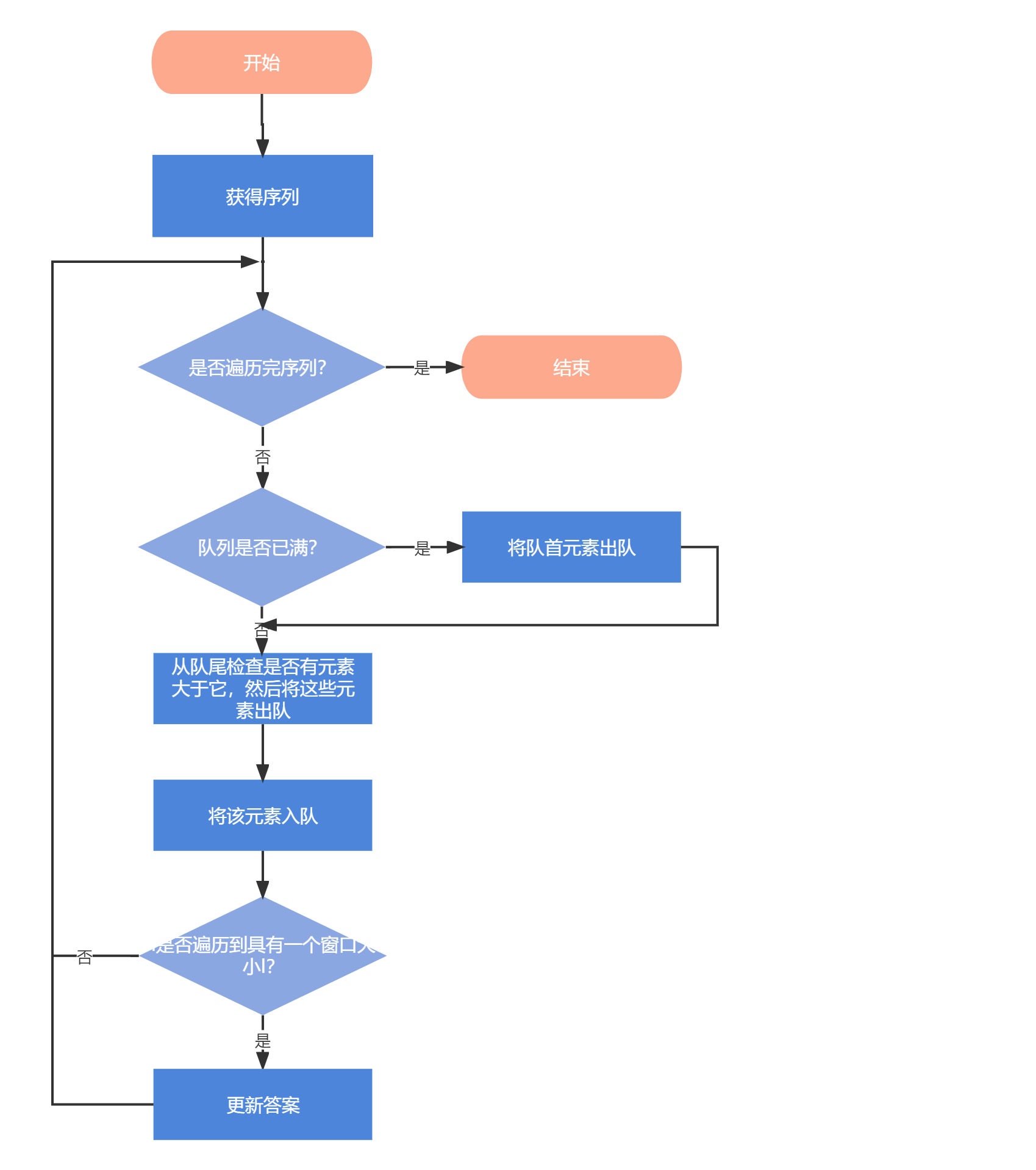
2.1.3 代码设计

int Find_Trough(int a[], int n, int l)
{
	deque<int> q;
	int result = 0;
	for (int i = 0; i < n; i++)
	{
		if (q.size() == l)
		{
			q.pop_front();		//弹出队首元素
		}
		if (q.empty())			//队列为空,直接插入元素
		{
			q.push_back(a[i]);
			continue;
		}
		while (!q.empty() && q.back() > a[i])
		{
			q.pop_back();		//弹出队尾元素
		}
		q.push_back(a[i]);		//将该元素入队
		if (i >= l - 1)			//当窗口长度等于l的时候可以更新答案
		{
			result = result < q.front() ? q.front() : result;		//若当前队首元素比result大,更新
		}
	}
	return result;
}

2.1.4 算法复杂度分析

滑动窗口法通过双端队列对序列元素进出，只需遍历一次序列即可，算法时间复杂度为$O(n)$，有较高的时间性能，且数据结构简洁。

2.2 分治法

2.2.1 算法思路

我们有以下结论：波谷的最大值在$[0,n/2-1],[n/2-l, n/2+l],[n/2,n-1]$这三个区间内取到。$[n/2-l, n/2+l]$区间较短，可以直接由滑动窗口法得到波谷的最大值，时间复杂度为$O(2l)$；当$[0,n/2-1],[n/2,n-1]$两个区间的长度小于$l$时，直接通过滑动窗口法求解即可；若大于等于$l$时，继续递归分割成三个区间，取最大值。由此得到答案。

2.2.2 算法图解

2.2.3 代码设计

int max(int a, int b, int c)
{
	if (a < b)
	{
		return b < c ? c : b;
	}
	else
	{
		return a < c ? c : a;
	}
}

int Sliding_window(int a[], int m, int n, int l)
{
	deque<int> q;
	int result = 0;
	for (int i = m; i <= n; i++)
	{
		if (q.size() == l)
		{
			q.pop_front();			//弹出队首元素
		}
		if (q.empty())				//队列为空,直接插入元素
		{
			q.push_back(a[i]);
			continue;
		}
		while (!q.empty() && q.back() > a[i])
		{
			q.pop_back();			//弹出队尾元素
		}
		q.push_back(a[i]);			//将该元素入队
		if (i >= l + n - m)			//当窗口长度等于l的时候可以更新答案
		{
			result = result < q.front() ? q.front() : result;		//若当前队首元素比result大,更新
		}
		else if (i == n)
		{
			result = q.front();		//还不够一个窗口长度且遍历到末尾,直接赋值
		}
	}
	return result;
}

int Find_Trough(int a[], int m, int n, int l)			// m,n 为左右边界
{
	if ((n - m) / 2 < l)
	{
		return max(Sliding_window(a, m, (n - m) / 2, l),
                   Sliding_window(a, (n - m) / 2, n, l));
	}
	return max(Find_Trough(a, m, (n - m) / 2, l), 
			   Find_Trough(a, (n - m) / 2, n, l), 
               Sliding_window(a, (n - m) / 2 - l, (n - m) / 2 + l, l));
}

2.2.4 算法复杂度分析

分治法通过将区间分割成三段，在$[0,n/2-1],[n/2-l, n/2+l],[n/2,n-1]$三个区间获得波谷的最大值，分割成三个子问题，其中两个区间继续分治，还有一个区间通过滑动窗口法直接求解，则$T(n)=2T(n/2)+O(2l)$，由替代法可知，算法时间复杂度为$O(n)$。

2.3 测试结果

多次测试，算法运行结果均正确，符合题意。

2.4 总结与讨论

我们对比以上两种算法的时间复杂度：

• 滑动窗口法：$T(n)=O(n)$
• 分治法：$T(n)=O(n)$

通过对以上两种算法时间复杂度的比较，以上两种算法均有$O(n)$的时间性能。滑动窗口法的思路较简单，且该思想在计算机网络通信等领域中被广泛采用，而分治法通过将问题分解成三个子问题进行求解，从而减小了问题的规模。

附：源代码

算法题1：

• 冒泡排序：

#include<iostream>
using namespace std;
const int N = 20;

void bubblesort(int a[], int k, int n)
{
	for (int i = 0; i < k; i++)
	{
		for (int j = n - 2; j >= i; j--)		//j控制每轮需要比较的次数 
		{
			if (a[j + 1] > a[j])				//不满足逆序要求，交换顺序 
			{
				int temp = a[j];
				a[j] = a[j + 1];
				a[j + 1] = temp;
			}
		}
	}
}

int main()
{
	int a[N], k, n;
	cout << "请输入元素个数与序列:" << endl;
	cin >> n;
	for (int i = 0; i < n; i++)
	{
		cin >> a[i];
	}
	cout << "请输入要获得的Top k个数" << endl;
	cin >> k;
	bubblesort(a, k, n);
	for (int i = 0; i < k; i++)
	{
		cout << a[i] << " ";
	}
	cout << endl;
	return 0;
}

• 堆排序：

#include<iostream>
#include<algorithm>
using namespace std;

const int N = 20;

void down(int u, int h[], int k)
{
    int t = u;	//t为点、左孩子、右孩子三个点中最小的一个点
    if (u * 2 <= k && h[u * 2] < h[t]) t = u * 2;
    if (u * 2 + 1 <= k && h[u * 2 + 1] < h[t]) t = u * 2 + 1;
    if (u != t)		//根节点不是最小的
    {
        //与最小的点交换
        swap(h[u], h[t]);
        down(t, h, k);	    //递归处理
    }
}

void up(int u, int h[], int k)
{
    while (u / 2 && h[u] < h[u / 2])
    {
        swap(h[u / 2], h[u]);
        u >>= 1;		    //u /= 2换上去
    }
}

void HeapSort(int h[], int k,int n)
{
    for (int i = k / 2; i; i--) down(i, h, k);	    //O(n)的时间复杂度将前k个元素建堆

    for (int i = k + 1; i <= n; i++)
    {
        if (h[i] > h[1])
        {
            h[1] = h[i];
            down(1, h, k);
        }
    }
}

int main()
{
    int h[N], k, n;
    cout << "请输入元素个数与序列:" << endl;
    cin >> n;
    for (int i = 1; i <= n; i++)
    {
        cin >> h[i];
    }
    cout << "请输入要获得的Top k个数" << endl;
    cin >> k;

    HeapSort(h, k, n);

    for (int i = k; i > 0; i--)
    {
        cout << h[i] << " ";
    }
    
    cout << endl;

    return 0;
}

• 减治法：

#include<iostream>
#include<algorithm>
using namespace std;
const int N = 20;

int Partition(int a[], int l, int r)
{
	int pivot = a[l];						// 取序列第一个元素为pivot
	int i = l, j = r + 1;
	do
	{
		do { i++; } while (a[i] > pivot);
		do { j--; } while (a[j] < pivot);
		if (i < j)  swap(a[i], a[j]);
	} while (i < j);

	return j;
}

void Top_k(int a[], int l, int r, int k)
{
	if (l >= r) return;
	int j = Partition(a, l, r);
	int count = j - l + 1;					// [l,j]区间共有多少数
	if (count == k)
	{
		return;
	}
	else if(count > k)
	{
		Top_k(a, l, j, k);					//前半部分第k大的数
	}
	else
	{
		Top_k(a, j + 1, r, k - count);		//后半部分第k - i大的数
	}
}

int main()
{
	int a[N], k, n;
	cout << "请输入元素个数与序列:" << endl;
	cin >> n;
	for (int i = 0; i < n; i++)
	{
		cin >> a[i];
	}
	cout << "请输入要获得的Top k个数" << endl;
	cin >> k;
	
	Top_k(a, 0, n - 1, k);

	for (int i = 0; i < k; i++)
	{
		cout << a[i] << " ";
	}
	cout << endl;
	return 0;
}

算法题2：

• 滑动窗口法：

#include<iostream>
#include<deque>
const int N = 20;
using namespace std;

int Find_Trough(int a[], int n, int l)
{
	deque<int> q;
	int result = 0;
	for (int i = 0; i < n; i++)
	{
		if (q.size() == l)
		{
			q.pop_front();			//弹出队首元素
		}
		if (q.empty())				//队列为空,直接插入元素
		{
			q.push_back(a[i]);
			continue;
		}
		while (!q.empty() && q.back() > a[i])
		{
			q.pop_back();			//弹出队尾元素
		}
		q.push_back(a[i]);			//将该元素入队
		if (i >= l - 1)				//当窗口长度等于l的时候可以更新答案
		{
			result = result < q.front() ? q.front() : result;		//若当前队首元素比result大,更新
		}
	}
	return result;
}

int main()
{
	int n, l, a[N];
	cout << "请输入序列的元素个数与序列各元素" << endl;
	cin >> n;
	for (int i = 0; i < n; i++)
	{
		cin >> a[i];
	}
	cout << "请输入求解波谷子序列的长度" << endl;
	cin >> l;
	int result = Find_Trough(a, n, l);
	cout << "序列中的" << l << "-序列的波谷的最大值为" << result << endl;
	return 0;
}

• 分治法：

#include<iostream>
#include<algorithm>
#include<deque>
const int N = 20;
using namespace std;

int max(int a, int b, int c)
{
	if (a < b)
	{
		return b < c ? c : b;
	}
	else
	{
		return a < c ? c : a;
	}
}

int Sliding_window(int a[], int m, int n, int l)
{
	deque<int> q;
	int result = 0;
	for (int i = m; i <= n; i++)
	{
		if (q.size() == l)
		{
			q.pop_front();			//弹出队首元素
		}
		if (q.empty())				//队列为空,直接插入元素
		{
			q.push_back(a[i]);
			continue;
		}
		while (!q.empty() && q.back() > a[i])
		{
			q.pop_back();			//弹出队尾元素
		}
		q.push_back(a[i]);			//将该元素入队
		if (i >= l + n - m)			//当窗口长度等于l的时候可以更新答案
		{
			result = result < q.front() ? q.front() : result;		//若当前队首元素比result大,更新
		}
		else if (i == n)
		{
			result = q.front();		//还不够一个窗口长度且遍历到末尾,直接赋值
		}
	}
	return result;
}

int Find_Trough(int a[], int m, int n, int l)			// m,n 为左右边界
{
	if ((n - m) / 2 < l)
	{
		return max(Sliding_window(a, m, (n - m) / 2, l), Sliding_window(a, (n - m) / 2, n, l));
	}
	return max(Find_Trough(a, m, (n - m) / 2, l), 
		Find_Trough(a, (n - m) / 2, n, l), Sliding_window(a, (n - m) / 2 - l, (n - m) / 2 + l, l));
}

int main()
{
	int n, l, a[N];
	cout << "请输入序列的元素个数与序列各元素" << endl;
	cin >> n;
	for (int i = 0; i < n; i++)
	{
		cin >> a[i];
	}
	cout << "请输入求解波谷子序列的长度" << endl;
	cin >> l;
	int result = Find_Trough(a, 0, n - 1, l);
	cout << "序列中的" << l << "-序列的波谷的最大值为" << result << endl;
	return 0;
}