算法课外思考题1007(二分查找比较与旋转有序序列)

💡Author：信安2002钱泽枢(ShiQuLiZhi)

🚀欢迎访问我的作业合集：https://sxhthreo.github.io/categories/%E4%BD%9C%E4%B8%9A/

一、二分查找与顺序查找比较

当二分查找算法至少执行多少次查找，相对于顺序查找才是有效的？

1.1 算法分析

由于二分查找算法要求序列是有序的，所以当获取一个无序序列时，二分查找算法需要先对序列进行排序，而后进行查找，但顺序查找可以对无序序列直接进行查找。

也就是说，设需要查找的元素个数为$x$时，二分查找的时间复杂度为$O(nlogn)+xO(log_2n)$，而顺序查找的时间复杂度为$xO(n)$。

我们要求满足$f(x)=k_1 nlogn+k_2 xlogn -k_3 x*n=0$时的$x$，$x_0=k\lfloor \frac{nlogn}{n-logn}\rfloor$，当$x>x_0$时，二分查找的时间性能优于顺序查找；否则二分查找的时间性能劣于顺序查找。

通过大量数据拟合可得，$k$取$8-10$之间。（抱歉，我想不出怎么证明这个的正确性……

1.2 代码设计

我们通过程序实际获取两种查找在查找一定数目元素时所需的时间。

代码测试由归并排序、二分查找、顺序查找、随机生成元素值等算法构成。

void merge_sort(int a[], int l, int r)
{
	if (l >= r) return;

	int mid = l + r >> 1, tmp[N];
	merge_sort(a, l, mid);
	merge_sort(a, mid + 1, r);

	int k = 0, i = l, j = mid + 1;
	while (i <= mid && j <= r)
		if (a[i] <= a[j]) tmp[k++] = a[i++];
		else tmp[k++] = a[j++];

	while (i <= mid) tmp[k++] = a[i++];
	while (j <= r) tmp[k++] = a[j++];

	for (i = l, j = 0; i <= r; i++, j++) a[i] = tmp[j];
}

int BinarySearch(int a[], int l, int r, int target) {
	if (l > r)
	{
		return -1;
	}
	else
	{
		int mid = (l + r) / 2;
		if (target < a[mid])
		{
			return BinarySearch(a, l, mid - 1, target);
		}
		else if (target > a[mid])
		{
			return BinarySearch(a, mid + 1, r, target);
		}
		else
		{
			return mid;
		}
	}
}

int SeqSearch(int a[], int n, int target)
{
	int i = n;
	a[0] = target;		//哨兵
	while (a[i] != target)
	{
		i--;
	}
	return i;
}

void Random(int a[], int n)			//生成区间在0-1000000的随机数 
{
	srand(time(0));					//设置时间种子
	for (int i = 1; i <= n; i++)
	{
		a[i] = rand() % 1000000;
	}
}

1.3 测试结果

运行结果如下：

需要查找1个元素时两算法的时间性能比较:执行二分查找算法时运行了139ms,执行顺序查找算法时运行了2ms
需要查找11个元素时两算法的时间性能比较:执行二分查找算法时运行了67ms,执行顺序查找算法时运行了15ms
需要查找21个元素时两算法的时间性能比较:执行二分查找算法时运行了68ms,执行顺序查找算法时运行了29ms
需要查找31个元素时两算法的时间性能比较:执行二分查找算法时运行了69ms,执行顺序查找算法时运行了48ms
需要查找41个元素时两算法的时间性能比较:执行二分查找算法时运行了70ms,执行顺序查找算法时运行了56ms
需要查找51个元素时两算法的时间性能比较:执行二分查找算法时运行了72ms,执行顺序查找算法时运行了73ms
需要查找61个元素时两算法的时间性能比较:执行二分查找算法时运行了74ms,执行顺序查找算法时运行了72ms
需要查找71个元素时两算法的时间性能比较:执行二分查找算法时运行了79ms,执行顺序查找算法时运行了89ms
需要查找81个元素时两算法的时间性能比较:执行二分查找算法时运行了76ms,执行顺序查找算法时运行了107ms
需要查找91个元素时两算法的时间性能比较:执行二分查找算法时运行了77ms,执行顺序查找算法时运行了117ms
需要查找101个元素时两算法的时间性能比较:执行二分查找算法时运行了79ms,执行顺序查找算法时运行了133ms
需要查找111个元素时两算法的时间性能比较:执行二分查找算法时运行了86ms,执行顺序查找算法时运行了145ms
需要查找121个元素时两算法的时间性能比较:执行二分查找算法时运行了87ms,执行顺序查找算法时运行了164ms
需要查找131个元素时两算法的时间性能比较:执行二分查找算法时运行了84ms,执行顺序查找算法时运行了174ms

可以发现，当在1000个元素组成的序列中需要查找的元素小于50个左右时，顺序查找所耗费的时间较短，50-60个元素左右则基本保持一致，大于70个元素二分查找所需时间明显小于顺序查找，且随着需要查找的元素的增加，两个算法耗费的时间差值愈大。当元素序列是10000个元素组成时则更加明显：

需要查找1个元素时两算法的时间性能比较:执行二分查找算法时运行了1634ms,执行顺序查找算法时运行了11ms
需要查找11个元素时两算法的时间性能比较:执行二分查找算法时运行了861ms,执行顺序查找算法时运行了121ms
需要查找21个元素时两算法的时间性能比较:执行二分查找算法时运行了857ms,执行顺序查找算法时运行了249ms
需要查找31个元素时两算法的时间性能比较:执行二分查找算法时运行了871ms,执行顺序查找算法时运行了395ms
需要查找41个元素时两算法的时间性能比较:执行二分查找算法时运行了870ms,执行顺序查找算法时运行了570ms
需要查找51个元素时两算法的时间性能比较:执行二分查找算法时运行了864ms,执行顺序查找算法时运行了621ms
需要查找61个元素时两算法的时间性能比较:执行二分查找算法时运行了870ms,执行顺序查找算法时运行了733ms
需要查找71个元素时两算法的时间性能比较:执行二分查找算法时运行了868ms,执行顺序查找算法时运行了834ms
需要查找81个元素时两算法的时间性能比较:执行二分查找算法时运行了869ms,执行顺序查找算法时运行了1099ms
需要查找91个元素时两算法的时间性能比较:执行二分查找算法时运行了872ms,执行顺序查找算法时运行了1291ms
需要查找101个元素时两算法的时间性能比较:执行二分查找算法时运行了885ms,执行顺序查找算法时运行了1385ms
需要查找111个元素时两算法的时间性能比较:执行二分查找算法时运行了872ms,执行顺序查找算法时运行了1349ms
需要查找121个元素时两算法的时间性能比较:执行二分查找算法时运行了882ms,执行顺序查找算法时运行了1549ms
需要查找131个元素时两算法的时间性能比较:执行二分查找算法时运行了881ms,执行顺序查找算法时运行了1729ms

1.4 总结与讨论

当数据量的大小和查找元素的个数不同时，我们所选取的查找算法不同。当数据量较小且序列无序时，我们可以使用顺序查找等算法；当数据量较大且查找的元素较多时，二分查找中需要耗费的由无序通过排序变成有序序列的时间可以分摊到每一个查找元素中，算法的时间性能较顺序查找将明显提高。我们应结合具体实际情况进行选择。

二、旋转有序序列

假设有一个旋转的有序序列（如12345678旋转后的一形态为56781234）。要求给出策略在此序列中查找某元素，分别返回其位置或失败标志。

2.1 二分查找+顺序查找

2.1.1 算法思路

我们先以没有重复元素进行分析：

可以看到，序列中间位置的两边必然有一边是有序的；我们记l为序列最左端位置，r为序列最右端位置，分三种情况进行讨论：

• a[mid] == target：直接返回mid位置即可
• a[mid] < a[r]：mid位置的右侧是有序的，意味着可以与右侧区间两端点进行比较判断目标值是否在该区间； 若目标值在右侧区间内，直接对右侧进行二分查找，否则对左侧进行查找
• a[mid] >= a[r]：mid位置的左侧是有序的，若目标值在左侧区间内，直接对左侧进行二分查找，否则对右侧进行查找

在这里，我们运用到了减治法的思想。但我们明显可以看到，当序列有重复元素时，则当a[mid] == a[l] == a[r]时，我们不能确定mid位置的左侧还是右侧是有序的，在本部分我们先采用顺序查找对整个序列进行遍历，时间代价为遍历整个序列所花费的时间。

2.1.2 算法图解

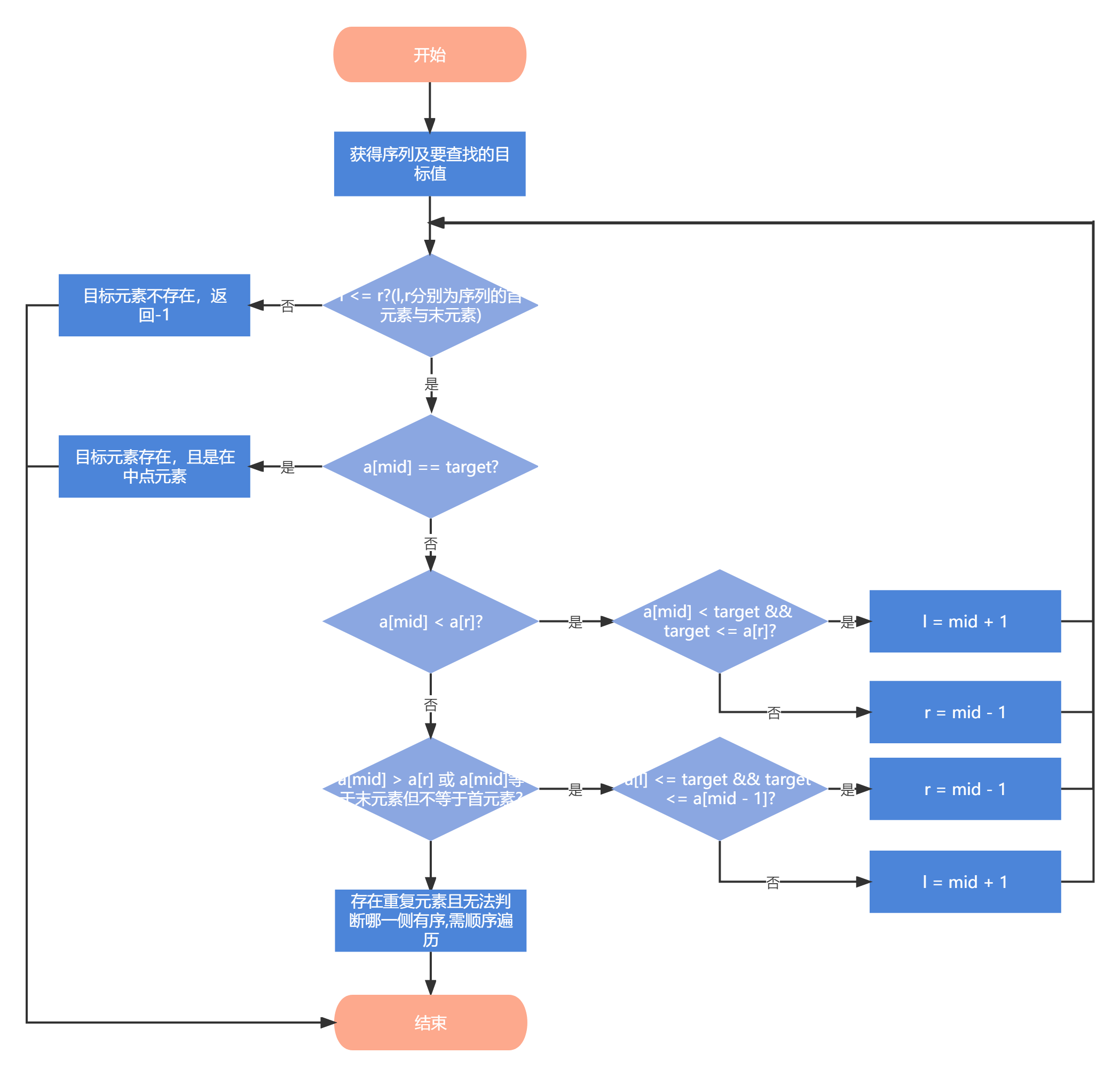
2.1.3 代码设计

int seq_find(int a[], int l, int r, int target)
{
	while (l <= r)
	{
		if (a[l] == target)
		{
			return l;
		}
		l++;
	}
	return -1;
}

int find(int a[], int n, int target)		// n为元素个数
{
	int l = 0, r = n - 1;
	while (l <= r)
	{
		int mid = (l + r) >> 1;
		// 中点就是要找的点
		if (a[mid] == target)
		{
			return mid;
		}
		// 右侧有序
		if (a[mid] < a[r])
		{
			if (a[mid] < target && target <= a[r])
			{
				l = mid + 1;
			}
			else
			{
				r = mid - 1;
			}
		}
		// 左侧有序
		else if (a[mid] > a[r] || (a[mid] == a[r] && a[mid] != a[l]))
		{
			if (a[l] <= target && target <= a[mid - 1])
			{
				r = mid - 1;
			}
			else
			{
				l = mid + 1;
			}
		}
		else
		{
			// 存在重复元素且无法判断哪一侧有序,需顺序遍历
			return seq_find(a, l, r, target);
		}
	}
	return -1;
}

2.1.4 算法复杂度分析

当序列有重复元素，存在a[mid] == a[l] == a[r]时，我们不能确定mid位置的左侧还是右侧是有序的，我们采用的是顺序查找对整个序列进行遍历，即最坏的情况将是对整个序列进行顺序遍历，算法时间复杂度为$O(n)$；当序列没有重复元素时，算法时间复杂度为二分查找的时间复杂度$O(log_2n)$。该算法的时间复杂度介于$O(log_2n)$和$O(n)$之间。

2.2 预处理+二分查找

2.2.1 算法思路

我们可以采用以下思路：先将序列的首元素与末元素进行比较，当相等时，删去末元素，直到序列的首元素与末元素不相等为止。虽然这样避免不了存在序列仍使得mid位置元素与末元素相等，如$[4,5,6,3,3,3,3]$等，但此时必然是右边完全是mid位置元素的重复，左侧是有序的。即若mid位置元素不是目标元素，则在左侧进行二分查找，我们完全可以归到左侧有序情况进行处理。

2.2.2 算法图解

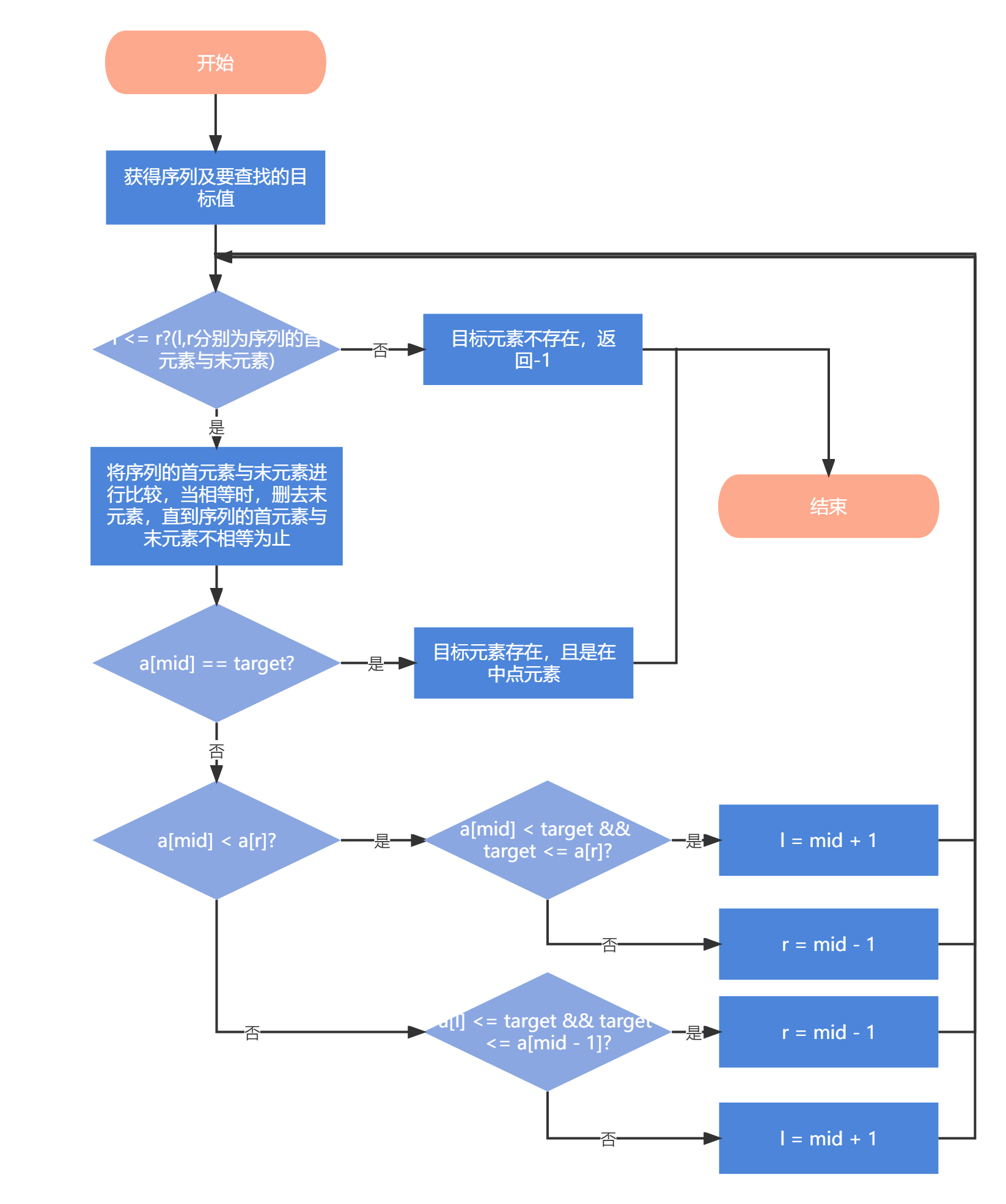
2.2.3 代码设计

int find(int a[], int n, int target)		// n为元素个数
{
	int l = 0, r = n - 1;
	while (l <= r)
	{
		while (a[l] == a[r] && l != r)		// 删去与首元素值相同的元素
		{
			r--;
		}
		int mid = (l + r) >> 1;
		// 中点就是要找的点
		if (a[mid] == target)
		{
			return mid;
		}
		// 右侧有序
		if (a[mid] < a[r])
		{
			if (a[mid] < target && target <= a[r])
			{
				l = mid + 1;
			}
			else
			{
				r = mid - 1;
			}
		}
		// 左侧有序 or 存在重复元素
		else
		{
			if (a[l] <= target && target <= a[mid - 1])
			{
				r = mid - 1;
			}
			else
			{
				l = mid + 1;
			}
		}
	}
	return -1;
}

2.2.4 算法复杂度分析

本算法通过先将序列的首元素与末元素进行比较，去除与首元素相同的末元素，则当出现重复元素时，可以判断出有序序列存在在哪一边，算法时间复杂度为二分查找的时间复杂度$O(log_2n)$。

2.4 测试结果

多次测试，算法运行结果均正确，符合题意。

2.5 总结与讨论

我们对比以上两种算法的时间复杂度：

• 二分查找+顺序查找：最坏$O(n)$
• 预处理+二分查找：$O(log_2n)$

通过对以上两种算法时间复杂度的比较，使用预处理+二分查找的时间性能是最优的。

在有序序列中的排序，我们首先考虑的当属二分查找。对有序序列进行旋转，可以得到两部分的有序序列，我们通过mid位置的元素，确定要继续查找的部分序列，运用到了减治法的思想。

实际上，无论旋转序列执行了几次旋转，总有$\lfloor n/2 \rfloor$个元素是有序的，都可以采用预处理+二分查找的方法在$O(log_2n)$的时间内找到目标元素。

附：源代码

算法题1：

#include<iostream>
#include<ctime>
using namespace std;
const int N = 1000;

void merge_sort(int a[], int l, int r)
{
	if (l >= r) return;

	int mid = l + r >> 1, tmp[N];
	merge_sort(a, l, mid);
	merge_sort(a, mid + 1, r);

	int k = 0, i = l, j = mid + 1;
	while (i <= mid && j <= r)
		if (a[i] <= a[j]) tmp[k++] = a[i++];
		else tmp[k++] = a[j++];

	while (i <= mid) tmp[k++] = a[i++];
	while (j <= r) tmp[k++] = a[j++];

	for (i = l, j = 0; i <= r; i++, j++) a[i] = tmp[j];
}

int BinarySearch(int a[], int l, int r, int target) {
	if (l > r)
	{
		return -1;
	}
	else
	{
		int mid = (l + r) / 2;
		if (target < a[mid])
		{
			return BinarySearch(a, l, mid - 1, target);
		}
		else if (target > a[mid])
		{
			return BinarySearch(a, mid + 1, r, target);
		}
		else
		{
			return mid;
		}
	}
}

int SeqSearch(int a[], int n, int target)
{
	int i = n;
	a[0] = target;		//哨兵
	while (a[i] != target)
	{
		i--;
	}
	return i;
}

void Random(int a[], int n)			//生成区间在0-1000000的随机数 
{
	srand(time(0));					//设置时间种子
	for (int i = 1; i <= n; i++)
	{
		a[i] = rand() % 1000000;
	}
}

int main()
{
	time_t begin, end;
	int a[N + 10];
	Random(a, N);
	srand(time(0));					//设置时间种子

	for (int i = 1; i < 500; i += 20)
	{
		begin = clock();
		// 二分查找
		merge_sort(a, 1, N);		//对序列进行排序
		int j = i;
		while (j--)
		{
			int target = a[rand() % N];		//随机选择一个数进行查找
			BinarySearch(a, 1, N, target);
		}
		end = clock();

		cout << "需要查找" << i << "个元素时两算法的时间性能比较:";
		cout << "执行二分查找算法时运行了" << double(end - begin) << "ms,";
		//顺序查找
		begin = clock();
		j = i;
		while (j--)
		{
			int target = a[rand() % N];		//随机选择一个数进行查找
			SeqSearch(a, N, target);
		}
		end = clock();
		cout << "执行顺序查找算法时运行了" << double(end - begin) << "ms" << endl;
	}
	return 0;
}

算法题2：

• 二分查找+顺序查找：

#include<iostream>
using namespace std;
const int N = 20;

int seq_find(int a[], int l, int r, int target)
{
	while (l <= r)
	{
		if (a[l] == target)
		{
			return l;
		}
		l++;
	}
	return -1;
}

int find(int a[], int n, int target)		// n为元素个数
{
	int l = 0, r = n - 1;
	while (l <= r)
	{
		int mid = (l + r) >> 1;
		// 中点就是要找的点
		if (a[mid] == target)
		{
			return mid;
		}
		// 右侧有序
		if (a[mid] < a[r])
		{
			if (a[mid] < target && target <= a[r])
			{
				l = mid + 1;
			}
			else
			{
				r = mid - 1;
			}
		}
		// 左侧有序
		else if (a[mid] > a[r] || (a[mid] == a[r] && a[mid] != a[l]))
		{
			if (a[l] <= target && target <= a[mid - 1])
			{
				r = mid - 1;
			}
			else
			{
				l = mid + 1;
			}
		}
		else
		{
			// 存在重复元素且无法判断哪一侧有序,需顺序遍历
			return seq_find(a, l, r, target);
		}
	}
	return -1;
}

int main()
{
	int n, a[N], target;
	cout << "请输入旋转有序序列的元素个数" << endl;
	cin >> n;
	for (int i = 0; i < n; i++)
	{
		cin >> a[i];
	}
	cout << "请输入要查找的元素" << endl;
	cin >> target;
	int result = find(a, n, target);
	if (result == -1)
	{
		cout << "没有这个元素!" << endl;
	}
	else
	{
		cout << "该元素在序列中的位序为" << result << endl;
	}
	return 0;
}

• 预处理+二分查找：

#include<iostream>
using namespace std;
const int N = 20;

int find(int a[], int n, int target)		// n为元素个数
{
	int l = 0, r = n - 1;
	while (l <= r)
	{
		while (a[l] == a[r] && l != r)		// 删去与首元素值相同的元素
		{
			r--;
		}
		int mid = (l + r) >> 1;
		// 中点就是要找的点
		if (a[mid] == target)
		{
			return mid;
		}
		// 右侧有序
		if (a[mid] < a[r])
		{
			if (a[mid] < target && target <= a[r])
			{
				l = mid + 1;
			}
			else
			{
				r = mid - 1;
			}
		}
		// 左侧有序 or 存在重复元素
		else
		{
			if (a[l] <= target && target <= a[mid - 1])
			{
				r = mid - 1;
			}
			else
			{
				l = mid + 1;
			}
		}
	}
	return -1;
}

int main()
{
	int n, a[N], target;
	cout << "请输入旋转有序序列的元素个数" << endl;
	cin >> n;
	for (int i = 0; i < n; i++)
	{
		cin >> a[i];
	}
	cout << "请输入要查找的元素" << endl;
	cin >> target;
	int result = find(a, n, target);
	if (result == -1)
	{
		cout << "没有这个元素!" << endl;
	}
	else
	{
		cout << "该元素在序列中的位序为" << result << endl;
	}
	return 0;
}