一、区间问题
1.1 例1:区间选点
给定 $N$ 个闭区间 $[a_i,b_i]$,请你在数轴上选择尽量少的点,使得每个区间内至少包含一个选出的点,输出选择的点的最小数量。
注:位于区间端点上的点也算作区间内。
算法步骤:
- 将每个区间按右端点从小到大排序
- 从前往后依次枚举每个区间
- 如果当前区间中已经包含点,则直接pass
- 如果当前区间中没有包含点,选择当前区间的右端点[选择当前的最好情况]
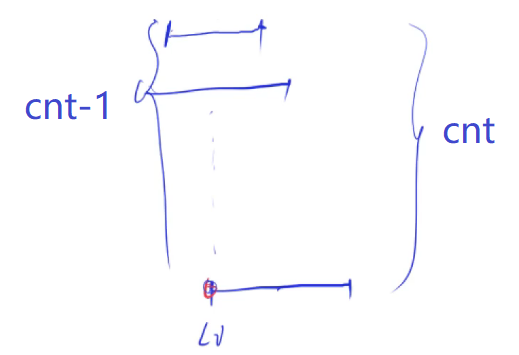
证明:
Case 1:$Ans\leq cnt$,其中$Ans$表示所有方案中的最小值,$cnt$表示一种可行解
Case 2:$Ans\geq cnt$,$Ans$至少要$cnt$个点覆盖掉$cnt$个区间
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010;
int n;
struct Range
{
int l, r;
bool operator< (const Range &W)const
{
return r < W.r;
}
}range[N];
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; i ++ ) scanf("%d%d", &range[i].l, &range[i].r);
sort(range, range + n);
int res = 0, ed = -2e9;
for (int i = 0; i < n; i ++ )
if (range[i].l > ed)
{
res ++ ;
ed = range[i].r;
}
printf("%d\n", res);
return 0;
}注:C++语法知识:
[1] 运算符重载:
返回类型 operator@ (参数表)const { // 函数体 }
const修饰函数,表明在该函数体内,不能修改对象的数据成员而且不能调用非const函数,用于保护数据。有两种条件时:
bool operator< (const location &W)const { if(path != W.path) return path < W.path; return id < W.id; // 路径相等按照序号排列 }[2]
sort函数的两个参数first,last,将[first, last)区间内元素升序排列。【注意区间为左闭右开】
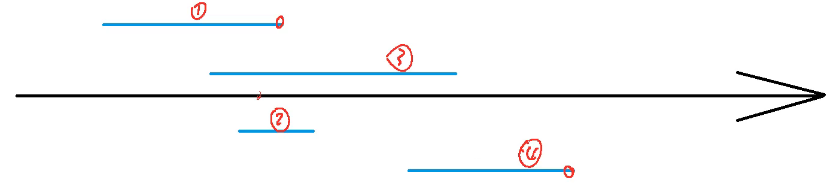
1.2 例2:区间分组
给定 $N$ 个闭区间 $[a_i,b_i]$,请你将这些区间分成若干组,使得每组内部的区间两两之间(包括端点)没有交集,并使得组数尽可能小。
输出最小组数。
算法步骤:
- 将每个区间按左端点从小到大排序
- 从前往后处理每个区间,依次判断能否将其放到某个现有的组中。若$L[i]<=Max_r(组中区间的最右端)$,则有交集
- 如果不存在这样的组,则开新组,然后再将其放进去
- 如果存在这样的组,将其放入组中,并更新当前组的$Max_r$
证明:
Case 1:$Ans\leq cnt$,其中$Ans$表示所有方案中的最小值,$cnt$表示一种可行解
Case 2:$Ans\geq cnt$,$cnt$区间有公共点
我们可以用一个小根堆来存储每个组的最大右端点值。
即若 $a[-1,1],b[2,3]$ 两个区间为一组,那么将该区间的最大右端点 3 放到小根堆内。
若目前查看的区间的左端点大于小根堆堆顶的值(range[i].l > heap.top()),那么至少说明,当前区间能放到这个组中,则将堆顶元素pop出来,堆中存入新的最大右端点代表这个组;
否则(heap.empty() || heap.top() >= r.l),需要新开一个组,直接将当前区间的右端点 push 进堆即可。
#include <iostream>
#include <algorithm>
#include <queue>
using namespace std;
const int N = 100010;
int n;
struct Range
{
int l, r;
bool operator< (const Range &W)const
{
return l < W.l;
}
}range[N];
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; i ++ )
{
int l, r;
scanf("%d%d", &l, &r);
range[i] = {l, r};
}
sort(range, range + n);
priority_queue<int, vector<int>, greater<int>> heap; // 小根堆
for (int i = 0; i < n; i ++ )
{
auto r = range[i];
if (heap.empty() || heap.top() >= r.l) heap.push(r.r); // 新的组
else
{
heap.pop(); // 堆顶删除
heap.push(r.r); // 新的右端点加到堆中
}
}
printf("%d\n", heap.size());
return 0;
}1.3 例3:区间覆盖
给定 $N$ 个闭区间 $[a_i,b_i]$ 以及一个线段区间 $[s,t]$,请你选择尽量少的区间,将指定线段区间完全覆盖。
输出最少区间数,如果无法完全覆盖则输出 $−1$。
算法步骤:
- 将每个区间按左端点从小到大排序
- 从前往后依次枚举每个区间,在所有能覆盖$start$的区间中,选择右端点最大的区间,然后将$start$更新成右端点的最大值
任何一最优解,都能通过替换变成算法得出来的解,每一步替换都是合法的,则$Ans = cnt$
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010;
int n;
struct Range
{
int l, r;
bool operator< (const Range &W)const
{
return l < W.l;
}
}range[N];
int main()
{
int st, ed;
scanf("%d%d", &st, &ed);
scanf("%d", &n);
for (int i = 0; i < n; i ++ )
{
int l, r;
scanf("%d%d", &l, &r);
range[i] = {l, r};
}
sort(range, range + n);
int res = 0;
bool success = false;
for (int i = 0; i < n; i ++ )
{
int j = i, r = -2e9;
while (j < n && range[j].l <= st) // 遍历所有左端点在start左边的区间,记录右端点的最大值
{
r = max(r, range[j].r);
j ++ ;
}
if (r < st) // 无解
{
res = -1;
break;
}
res ++ ;
if (r >= ed)
{
success = true;
break;
}
st = r;
i = j - 1;
}
if (!success) res = -1;
printf("%d\n", res);
return 0;
}二、Huffman树
#include <iostream>
#include <algorithm>
#include <queue>
using namespace std;
int main()
{
int n;
scanf("%d", &n);
priority_queue<int, vector<int>, greater<int>> heap;
while (n -- )
{
int x;
scanf("%d", &x);
heap.push(x);
}
int res = 0;
while (heap.size() > 1)
{
int a = heap.top(); heap.pop(); // 取出最小的两个元素
int b = heap.top(); heap.pop();
res += a + b;
heap.push(a + b);
}
printf("%d\n", res);
return 0;
}三、不等式
3.1 排序不等式
有 $n$ 个人排队到 $1$ 个水龙头处打水,第 $i$ 个人装满水桶所需的时间是 $t_i$,请问如何安排他们的打水顺序才能使所有人的等待时间之和最小。
每个人耗的时间分别为$t_1,t_2,…,t_n$,则总时间=$t_1(n-1)+t_2(n-2)+…+0$
按照从小到大的顺序排队,总时间最小。
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 100010;
int n;
int t[N];
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; i ++ ) scanf("%d", &t[i]);
sort(t, t + n);
reverse(t, t + n);
LL res = 0;
for (int i = 0; i < n; i ++ ) res += t[i] * i; // 不reverse则每次乘n - i + 1
printf("%lld\n", res);
return 0;
}3.2 绝对值不等式
在一条数轴上有 $N$ 家商店,它们的坐标分别为 $A_1\sim A_N$。
现在需要在数轴上建立一家货仓,每天清晨,从货仓到每家商店都要运送一车商品。
为了提高效率,求把货仓建在何处,可以使得货仓到每家商店的距离之和最小。
$f(x)=|x_1-x|+|x_2-x|+…+|x_n-x|$的最小值
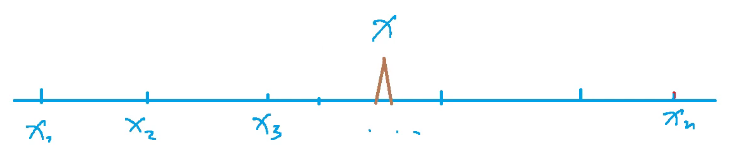
分组思想:
$f(x)=|x_1-x|+|x_2-x|+…+|x_n-x|\\=(|x_1-x|+|x_n-x|)+(|x_2-x|+|x_{n-1}-x|)+…\\\geq x_n-x_1+x_{n-1}-x_{2}+…$
当$x$取到中位数时(或中间两个数之间),可以取到等号
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010;
int n;
int q[N];
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; i ++ ) scanf("%d", &q[i]);
sort(q, q + n);
int res = 0;
for (int i = 0; i < n; i ++ ) res += abs(q[i] - q[n / 2]);
printf("%d\n", res);
return 0;
}四、推公式
农民约翰的 $N$ 头奶牛(编号为 $1…N$)计划逃跑并加入马戏团,为此它们决定练习表演杂技。
奶牛们不是非常有创意,只提出了一个杂技表演:
叠罗汉,表演时,奶牛们站在彼此的身上,形成一个高高的垂直堆叠。
奶牛们正在试图找到自己在这个堆叠中应该所处的位置顺序。
这 $N$ 头奶牛中的每一头都有着自己的重量 $W_i$ 以及自己的强壮程度 $S_i$。
一头牛支撑不住的可能性取决于它头上所有牛的总重量(不包括它自己)减去它的身体强壮程度的值,现在称该数值为风险值,风险值越大,这只牛撑不住的可能性越高。
任务是确定奶牛的排序,使得所有奶牛的风险值中的最大值尽可能的小。
结论:按照$W_i+S_i$从小到大的顺序排,最大的危险系数一定是最小的。
证明:
贪心得到的答案 >= 最优解
贪心得到的答案 <= 最优解
假设不按照此顺序排序,则必然存在有$W_i+S_i>W_{i+1}+S_{i+1}$
| | 第i个位置上的牛 | 第i+1个位置上的牛 |
| :——: | :—————————————-: | :———————————————-: |
| 交换前 | $W_1+W_2+…+W_{i-1}-S_i$ | $W_1+W_2+…+W_i-S_{i+1}$ |
| 交换后 | $W_1+W_2+…+W_{i-1}-S_{i+1}$ | $W_1+W_2+…+W_{i-1}+W_{i+1}-S_i$ |将$W_1+…+W_{i-1}$删去并同时增加$S_i+S_{i+1}$项,整理得到:
| | 第i个位置上的牛 | 第i+1个位置上的牛 |
| :——: | :——————-: | :———————-: |
| 交换前 | $S_{i+1}$ | $W_{i}+S_{i}$ |
| 交换后 | $S_{i}$ | $W_{i+1}+S_{i+1}$ |最大值都不会变大
#include <iostream>
#include <algorithm>
using namespace std;
typedef pair<int, int> PII;
const int N = 50010;
int n;
PII cow[N];
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; i ++ )
{
int s, w;
scanf("%d%d", &w, &s);
cow[i] = {w + s, w};
}
sort(cow, cow + n);
int res = -2e9, sum = 0;
for (int i = 0; i < n; i ++ )
{
int s = cow[i].first - cow[i].second, w = cow[i].second;
res = max(res, sum - s);
sum += w;
}
printf("%d\n", res);
return 0;
}