算法课外思考题1019(芯片设计)

💡Author：信安2002钱泽枢(ShiQuLiZhi)

🚀欢迎访问我的作业合集：https://sxhthreo.github.io/categories/%E4%BD%9C%E4%B8%9A/

1 题目描述

在芯片设计中，经常要考虑输入与输出端之间的连接关系，假设输入与输出端分别有若干端口，并且用一组数字进行标注（可能有重复），当且仅当输入端与输出端数字相等并且不与其他连接线相交的情况下，可以建立输入与输出之间的连接。设计算法策略，计算可能得到的最大连接数。

2 算法思路

本题的描述中，需要找到两序列中数字相等且不相交的端口的最大连接数，故可以抽象为最长公共子序列问题，可以用动态规划求解，问题共有$\theta(n^2)$个子问题。

• 状态表示$f(i,j)$：

  • 集合
    • 所有在第一个序列的前$i$个端口中出现，且在第二个序列的前$j$个端口中出现的子序列
  • 属性：$Max$(最大连接数)

• 状态计算：

  • 集合划分——$f(i,j)$

  • 以$a[i],b[j]$是否出现进行划分：

    

其中：

• $f(i-1,j)$包含01情况，可以直接以其作为代表；

• $f(i-1,j)$和$f(i,j-1)$包含00情况$f(i-1,j-1)$，则可以不计算$f(i-1,j-1)$；

• 当$a[i] == b[j]$时，有$f[i,j]=max(f[i][j], f[i - 1][j - 1] + 1)$。

3 算法图解

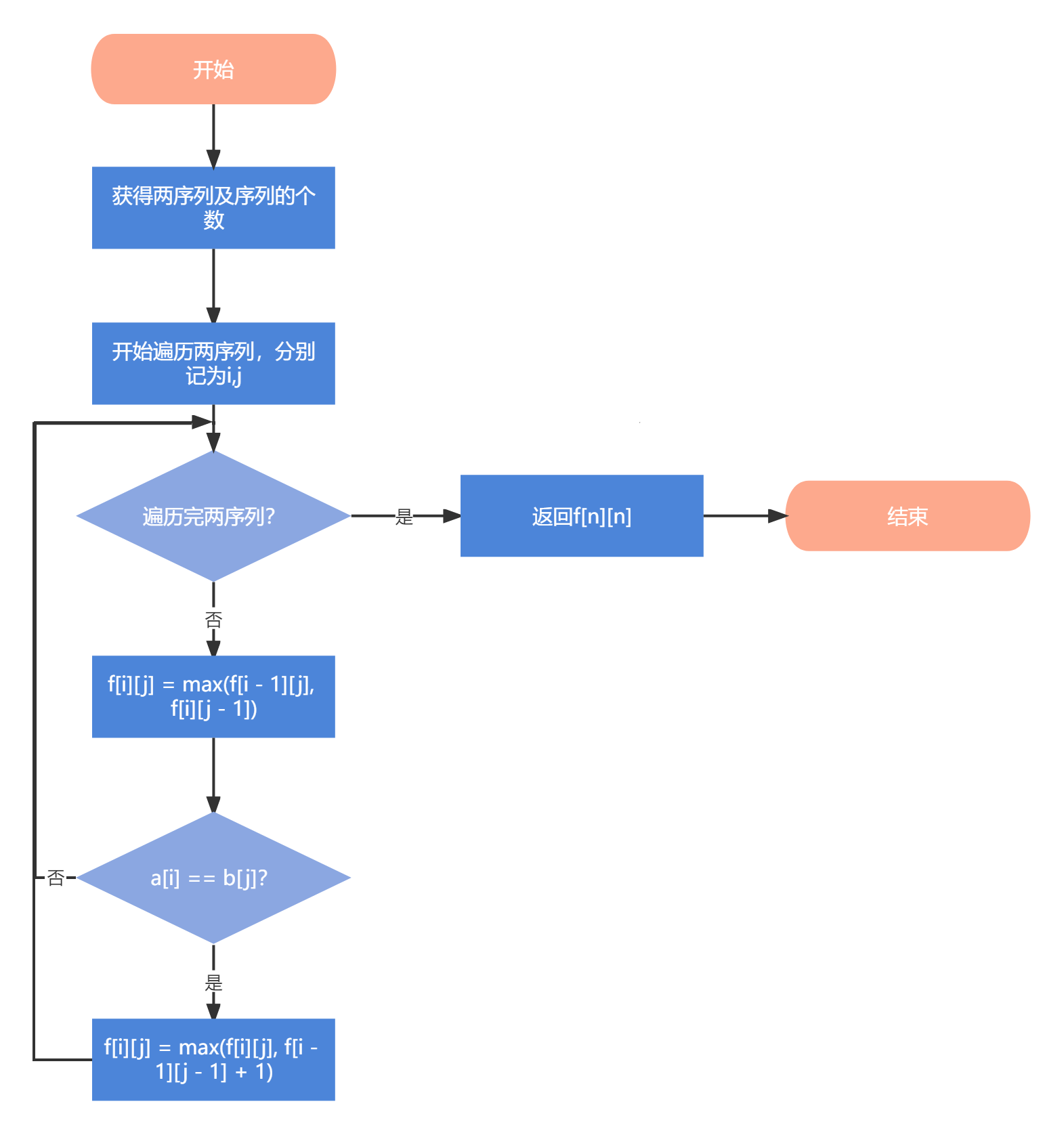
4 代码设计

int work(int a[], int b[], int n)
{
	int f[N][N] = {0};		// 动态规划建立的数组
	for (int i = 1; i <= n; i++)
	{
		for (int j = 1; j <= n; j++)
		{
			f[i][j] = max(f[i - 1][j], f[i][j - 1]);
			if (a[i] == b[j]) f[i][j] = max(f[i][j], f[i - 1][j - 1] + 1);
		}
	}

	return f[n][n];
}

5 测试结果

多次测试，算法运行结果均正确，符合题意。

6 总结与讨论

该算法通过二重循环求解答案，算法时间复杂度为$O(n^2)$

本题最重要的环节是建模为一个动态规划问题。最长公共子序列问题是动态规划问题中的一类经典问题，有较多变式，本题就是其中一例。我们还可以通过打印中间结果判断最大连接的序列。

附：源代码

#include<iostream>
using namespace std;
const int N = 20;

int work(int a[], int b[], int n)
{
	int f[N][N] = {0};		// 动态规划建立的数组
	for (int i = 1; i <= n; i++)
	{
		for (int j = 1; j <= n; j++)
		{
			f[i][j] = max(f[i - 1][j], f[i][j - 1]);
			if (a[i] == b[j]) f[i][j] = max(f[i][j], f[i - 1][j - 1] + 1);
		}
	}

	return f[n][n];
}

int main()
{
	int n, a[N], b[N];
	cout << "请输入芯片端口个数:" << endl;
	cin >> n;
	cout << "请输入各端口的数字:" << endl;
	for (int i = 1; i <= n; i++)
	{
		cin >> a[i];
	}
	for (int i = 1; i <= n; i++)
	{
		cin >> b[i];
	}
	cout << "最大的连接数为" << work(a, b, n) << endl;
	return 0;
}