💡Author:信安2002钱泽枢(ShiQuLiZhi)
🚀欢迎访问我的作业合集:https://sxhthreo.github.io/categories/%E4%BD%9C%E4%B8%9A/
一、最大子矩阵和问题
给定一个m行n列的整数矩阵A,试求矩阵A的一个子矩阵,使其各元素之和为最大。
1.1 前缀和+穷举法
1.1.1 算法思路
定义一个二维数组s[][] , s[i][j] 表示二维数组中,左上角(1, 1)到右下角(i, j)所包围的矩阵元素的和。然后我们推导二维前缀和的公式。
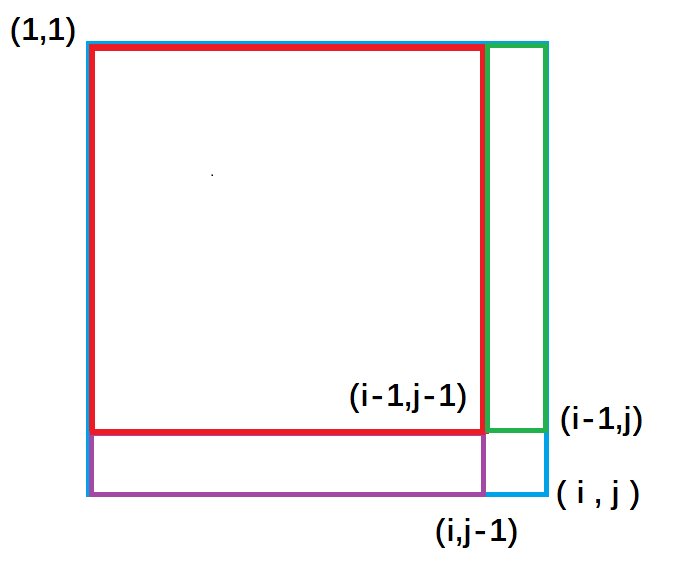
紫色面积是指(1, 1)左上角到(i, j - 1)右下角的矩形面积, 绿色面积是指(1, 1)左上角到(i - 1, j)右下角的矩形面积。每一个颜色的矩形面积都代表了它所包围元素的和。

从图中我们很容易看出,整个外围蓝色矩形面积s[i][j] = 绿色面积s[i - 1][j] + 紫色面积s[i][j - 1] - 重复加的红色的面积s[i - 1][j - 1] + 小方块的面积a[i][j]。
s[i, j]= 第i行j列格子左上部分所有元素的和s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j]
则我们可以推导出子矩阵的和的公式:
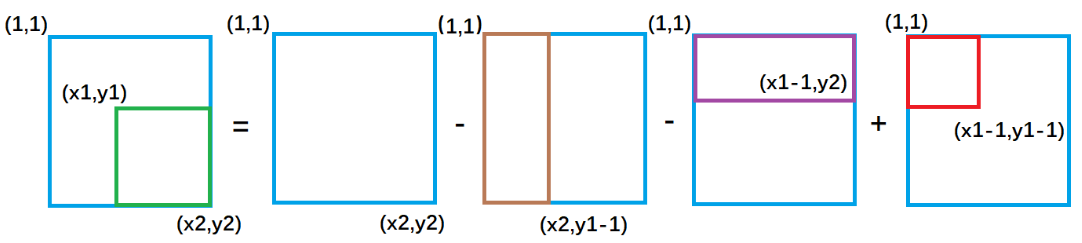
以
(x1, y1)为左上角,(x2, y2)为右下角的子矩阵的和为:s[x2, y2] - s[x1 - 1, y2] - s[x2, y1 - 1] + s[x1 - 1, y1 - 1]
我们可以采用穷举各个左上角及右下角坐标的方式,来获得最大的子矩阵和。
1.1.2 代码设计
void presum(int n, int m)
{
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
//求前缀和
s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j];
}
void max_matrix_sum(int n, int m)
{
int x1, y1, x2, y2, max = 0;
for (int i = 1; i <= n; i++) // x1
{
for (int j = 1; j <= m; j++) // y1
{
for (int k = i; k <= n; k++) // x2
{
for (int z = j; z <= m; z++) // y2
{
int sum = s[k][z] - s[i - 1][z] - s[k][j - 1] + s[i - 1][j - 1];
if (max < sum)
{
x1 = i, y1 = j, x2 = k, y2 = z;
max = sum;
}
}
}
}
}
cout << "最大的子矩阵和为" << max << ",左上角坐标为(" << x1 << ","
<< y1 << "),右下角坐标为(" << x2 << "," << y2 << ")" << endl;
}1.1.3 算法复杂度分析
穷举的时间复杂度为$O(n^4)$,处理各个左下角及右下角坐标所形成的子矩阵和的时间复杂度为$O(1)$,则算法的时间复杂度为$O(n^4)$,算法时间复杂度有待提升。
需要注意的是,虽然前缀和手段在这里计算最大子矩阵和的时间复杂度较高,但当给定左上角和右下角坐标的情况下计算子矩阵的和的时间复杂度仅为$O(1)$,在部分场景中的时间效率很高。
1.2 动态规划算法
1.2.1 算法思路
我们考虑一维的最大子段和问题:
给出一个序列a[0], a[1], a[2], ... , a[n],求出连续的子段使其总和最大。
我们记a[i]表示第i个元素,dp[i]表示以a[i]结尾的最大子段和,有以下两种情况:
- 若
dp[i-1] > 0,则dp[i] = dp[i-1] + a[i] - 若
dp[i-1] < 0,则dp[i] = a[i]
则有dp[i] = max{a[i], dp[i-1] + a[i]}
扩大到二维子矩阵和的问题,我们可以遍历所有行(分别有起始行、终点行),并将行间范围内的每列加和,然后就能转化为最大字段和问题。在求解过程中,需要记录每次行间范围内能得到的最大字段和、起始左区间和终止右区间,并通过比较最终获得矩阵的最大子矩阵和。
1.2.2 代码设计
pair<pair<int,int>,int> sum_work(int m)
{
int dp = 0, max = 0;
int al, ar, l, r; // i,j表示字段和的起始和终止坐标, al,ar表示答案
for (int i = 1; i <= m; i++)
{
if (dp > 0)
{
r++;
dp += row[i];
}
else
{
l = r = i; // 将新一段字段和起始和终止坐标记录
dp = row[i];
}
if (max < dp)
{
max = dp;
al = l, ar = r;
}
}
return { {al,ar},max };
}
void max_matrix_sum(int n, int m)
{
int max = 0, s, t, l, r; // a, b记录起始和终点行
pair<pair<int, int>, int> answer;
for (int i = 1; i <= n; i++) // 第i行
{
memset(row, 0, sizeof(row)); // 将row数组清零
for (int j = i; j <= n; j++) // 第j行
{
// 将两行范围内的每列加和
for (int k = 1; k <= m; k++)
{
row[k] += a[j][k];
}
// 求最大字段和
answer = sum_work(m);
if (max < answer.second)
{
l = answer.first.first;
r = answer.first.second;
s = i, t = j; // 记录答案的起始行和终点行
max = answer.second;
}
}
}
cout << "最大的子矩阵和为" << max << ",左上角坐标为(" << s << ","
<< l << "),右下角坐标为(" << t << "," << r << ")" << endl;
}1.2.3 算法复杂度分析
动态规划算法中需要进行三重循环,其中需要分别遍历所有行(分别有起始行、终点行)、将两行范围内的每列加和、求最大字段和,时间复杂度为$O(n^3)$,较前缀和+穷举法的时间性能有所提升。
1.3 测试结果

多次测试,算法运行结果均正确,符合题意。
1.4 总结与讨论
我们对比以上两种算法的时间复杂度:
- 前缀和+穷举法:$O(n^4)$
- 动态规划算法:$O(n^3)$
通过对以上两种算法时间复杂度的比较,使用动态规划算法的时间性能是最优的。
降维是算法设计中的一个重要手段。当看到二维问题时,可以通过将其降维来转化为一个我们熟悉的问题或模型,从而设计出合适的算法。
二、遗产分割问题
John有两个孩子,在John病逝后,留下了一组价值不一定相同的魔卡,现在要求你设计一种策略,帮John的经管人将John的这些遗产分给他的两个孩子,使得他们获得的遗产差异最小(魔卡不能分拆)。
2.1 算法思路
我们可以通过01背包问题的思想求解本题,只需求解其中一个孩子分配的遗产,就能推算出另一个孩子分配到的遗产。
- 背包的体积为 $total / 2$ ( $total$ 表示所有魔卡的价值总和)
- 背包要放入的魔卡(集合里的元素)的价值和体积均为魔卡价值的数值
- 背包中每一个元素不可重复放入
我们分析该问题的状态表示和状态转移方程:
- 状态表示$f(i,j)$:
- 集合
- 所有选法
- 条件:(1)只从前 $i$ 个魔卡中选; (2)总魔卡价值$\leq j$
- 属性:在最多只能拿 $total / 2$ 的价值的条件下获得的最大魔卡价值$Max$
- 集合
- 状态计算:集合划分——$f(i,j)$
- 不含第 $i$ 个魔卡:$f(i-1,j)$
- 含第 $i$ 个魔卡:$f(i-1,j-w_i)+w_i$
故有:$f(i,j) = Max(f(i-1,j),f(i-1,j-w_i)+w_i)$
其中,01背包问题的状态表示数组可以优化为一维求解。
通过动态规划求解出的结果就是其中一个孩子得到的魔卡总价值$f(total/2)$, 另一个孩子得到的魔卡总价值则是$total-f(total/2)$。
每次更新 $f(j)$ 数组时,应记录对应选定的魔卡序号,则可以遍历价值从 $f(total/2)$ 到最小价值的记录数组依次输出其中一个孩子分配到的各个魔卡价值,并将这些价值置为 $0$ ,然后遍历所有非 $0$ 的价值则为另一个孩子分配到的各个魔卡价值。
2.2 算法图解

2.3 代码设计
void distribute(int n, int total)
{
// 背包问题获得 total / 2 背包空间内的最大价值
for (int i = 1; i <= n; i++)
{
for (int j = total / 2; j >= w[i]; j--)
{
if (f[j] < f[j - w[i]] + w[i])
{
f[j] = f[j - w[i]] + w[i];
num[j] = i; // 记录对应选定的魔卡序号
}
}
}
cout << "魔卡分配依次为" << f[total / 2] << "与" << total - f[total / 2] << endl;
// 输出第一个孩子分配到的魔卡
cout << "第一个孩子分配到的魔卡依次为:";
int j = f[total / 2];
while (j > 0 && num[j] != 0)
{
cout << w[num[j]] << " ";
int res = w[num[j]];
w[num[j]] = 0; // 标记该魔卡被分配给第一个孩子
j -= res;
}
cout << endl;
// 输出第二个孩子分配到的魔卡
cout << "第二个孩子分配到的魔卡依次为:";
for (int i = 1; i <= n; i++)
{
if (w[i] != 0)
{
cout << w[i] << " ";
}
}
cout << endl;
}2.4 测试结果



多次测试,算法运行结果均正确,符合题意。
2.5 总结与讨论
通过将遗产分配问题转化为01背包问题,该问题迎刃而解,算法的时间复杂度为$O(n^2)$
通过滚动数组进行动态规划,可以减小算法设计所需的空间,算法总体的复杂度均较低。
01背包问题在具体的场景中有着广泛的应用。本题的算法设计,让我对01背包问题的算法思路与具体求解方法有了更深层次的理解,同时背包问题还有完全背包、多重背包、分组背包等不同形式,我将进一步学习并掌握其建模手段。
附:源代码
算法题1
法1:前缀和+穷举法
#include<iostream>
const int N = 1010;
using namespace std;
int a[N][N], s[N][N];
void presum(int n, int m)
{
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
//求前缀和
s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j];
}
void max_matrix_sum(int n, int m)
{
int x1, y1, x2, y2, max = 0;
for (int i = 1; i <= n; i++) // x1
{
for (int j = 1; j <= m; j++) // y1
{
for (int k = i; k <= n; k++) // x2
{
for (int z = j; z <= m; z++) // y2
{
int sum = s[k][z] - s[i - 1][z] - s[k][j - 1] + s[i - 1][j - 1];
if (max < sum)
{
x1 = i, y1 = j, x2 = k, y2 = z;
max = sum;
}
}
}
}
}
cout << "最大的子矩阵和为" << max << ",左上角坐标为(" << x1 << ","
<< y1 << "),右下角坐标为(" << x2 << "," << y2 << ")" << endl;
}
int main()
{
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
cin >> a[i][j];
presum(n, m); // 求前缀和
max_matrix_sum(n, m); // 求最大子矩阵和
return 0;
}法2:动态规划算法
#include<iostream>
#include<utility>
const int N = 1010;
using namespace std;
int a[N][N], row[N];
pair<pair<int,int>,int> sum_work(int m)
{
int dp = 0, max = 0;
int al, ar, l, r; // i,j表示字段和的起始和终止坐标, al,ar表示答案
for (int i = 1; i <= m; i++)
{
if (dp > 0)
{
r++;
dp += row[i];
}
else
{
l = r = i; // 将新一段字段和起始和终止坐标记录
dp = row[i];
}
if (max < dp)
{
max = dp;
al = l, ar = r;
}
}
return { {al,ar},max };
}
void max_matrix_sum(int n, int m)
{
int max = 0, s, t, l, r; // a, b记录起始和终点行
pair<pair<int, int>, int> answer;
for (int i = 1; i <= n; i++) // 第i行
{
memset(row, 0, sizeof(row)); // 将row数组清零
for (int j = i; j <= n; j++) // 第j行
{
// 将两行范围内的每列加和
for (int k = 1; k <= m; k++)
{
row[k] += a[j][k];
}
// 求最大前缀和
answer = sum_work(m);
if (max < answer.second)
{
l = answer.first.first;
r = answer.first.second;
s = i, t = j; // 记录答案的起始行和终点行
max = answer.second;
}
}
}
cout << "最大的子矩阵和为" << max << ",左上角坐标为(" << s << ","
<< l << "),右下角坐标为(" << t << "," << r << ")" << endl;
}
int main()
{
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
cin >> a[i][j];
max_matrix_sum(n, m); // 求最大子矩阵和
return 0;
}算法题2
#include<iostream>
#include<algorithm>
#include<set>
using namespace std;
const int N = 1010;
int w[N];
int f[N], num[N];
void distribute(int n, int total)
{
for (int i = 1; i <= n; i++)
{
for (int j = total / 2; j >= w[i]; j--)
{
if (f[j] < f[j - w[i]] + w[i])
{
f[j] = f[j - w[i]] + w[i];
num[j] = i; // 记录对应选定的魔卡序号
}
}
}
cout << "魔卡分配依次为" << f[total / 2] << "与" << total - f[total / 2] << endl;
// 输出第一个孩子分配到的魔卡
cout << "第一个孩子分配到的魔卡依次为:";
int j = f[total / 2];
while (j > 0 && num[j] != 0)
{
cout << w[num[j]] << " ";
int res = w[num[j]];
w[num[j]] = 0; // 标记该魔卡被分配给第一个孩子
j -= res;
}
cout << endl;
// 输出第二个孩子分配到的魔卡
cout << "第二个孩子分配到的魔卡依次为:";
for (int i = 1; i <= n; i++)
{
if (w[i] != 0)
{
cout << w[i] << " ";
}
}
cout << endl;
}
int main()
{
int n, total = 0; // n为背包大小
memset(num, 0, sizeof(num));
cin >> n;
for (int i = 1; i <= n; i++)
{
cin >> w[i]; // w[i]为魔盒价值
total += w[i];
}
distribute(n, total);
return 0;
}
