作业

发布日期: 2022-11-02

更新日期: 2022-11-04

文章字数: 6.7k

阅读时长: 36 分

💡Author：信安2002钱泽枢(ShiQuLiZhi)

🚀欢迎访问我的作业合集(部分文章Latex语法支持不佳QAQ)：https://sxhthreo.github.io/categories/%E4%BD%9C%E4%B8%9A/

一、矩阵的LU分解

调研学习并给出矩阵的LU分解方法。

1.1 Doolittle(杜利特尔)直接分解法

假设 $A$ 的各阶顺序主子式 $D_i\neq 0(i=1:n)$，则 $A=LU$，记

$\left(\begin{array}{cccc}
a_{11} & a_{12} & \cdots & a_{1 n} \\
a_{21} & a_{22} & \cdots & a_{2 n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{n 1} & a_{n 2} & \cdots & a_{n n}
\end{array}\right)=\left(\begin{array}{cccc}
1 & & & \\
l_{21} & 1 & & \\
\vdots & \vdots & \ddots & \\
l_{n 1} & l_{n 2} & \cdots & 1
\end{array}\right)\left(\begin{array}{cccc}
u_{11} & u_{12} & \cdots & u_{1 n} \\
& u_{22} & \cdots & u_{2 n} \\
& & \ddots & \vdots \\
& & & u_{n n}
\end{array}\right)$

由矩阵乘法，得

$\left\{\begin{array}{l}
\boldsymbol{u}_{1 j}=\boldsymbol{a}_{1 j}, j=\mathbf{1}: \boldsymbol{n} \\
\boldsymbol{l}_{i 1}=\boldsymbol{a}_{i 1} / \boldsymbol{u}_{11}, i=\mathbf{2}: \boldsymbol{n}
\end{array}\right.$及$\left\{\begin{array}{l}
\boldsymbol{u}_{i j}=\boldsymbol{a}_{i j}-\sum_{k=1}^{i-1} \boldsymbol{l}_{i k} \boldsymbol{u}_{k j} \quad j=\boldsymbol{i}: \boldsymbol{n} \\
\boldsymbol{l}_{i j}=\left(\boldsymbol{a}_{i j}-\sum_{k=1}^{j-1} \boldsymbol{l}_{i k} \boldsymbol{U}_{k j}\right) / \boldsymbol{u}_{i j} \quad \boldsymbol{i}=\boldsymbol{j}+\mathbf{1}: \boldsymbol{n}
\end{array}\right.$

该分解称为Doolittle直接分解法。紧凑格式如下：

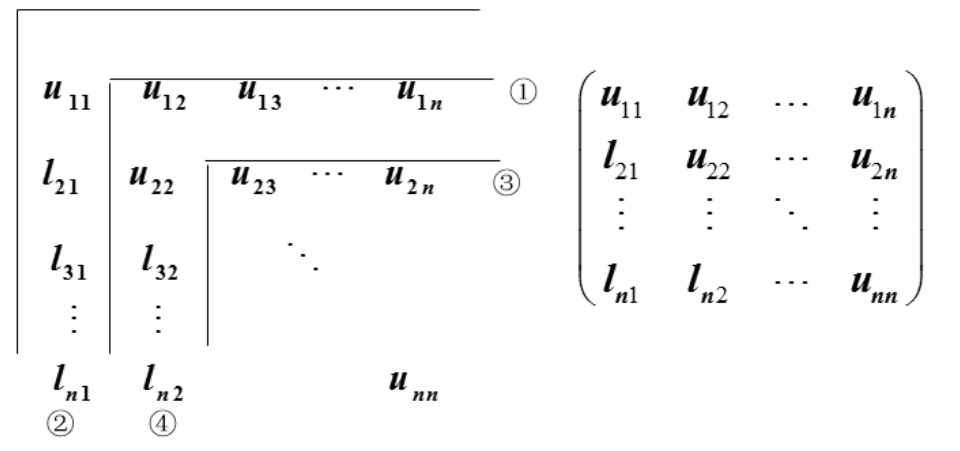
image-紧凑格式

如，解线性方程组$\left[\begin{array}{llll}
1 & 0 & 2 & 0 \\
0 & 1 & 0 & 1 \\
1 & 2 & 4 & 3 \\
0 & 1 & 0 & 3
\end{array}\right]\left[\begin{array}{l}
x_{1} \\
x_{2} \\
x_{3} \\
x_{4}
\end{array}\right]=\left[\begin{array}{c}
5 \\
3 \\
17 \\
7
\end{array}\right]$

得到$A=\left[\begin{array}{llll}
1 & & & \\
0 & 1 & & \\
1 & 2 & 1 & \\
0 & 1 & 0 & 1
\end{array}\right]\left[\begin{array}{llll}
1 & 0 & 2 & 0 \\
& 1 & 0 & 1 \\
& & 2 & 1 \\
& & & 2
\end{array}\right]$

解 $Ly=b$，得 $y=(5,3,6,4)^{T}$；解 $Ux=y$，得 $x=(1,1,2,2)^{T}$

在实际代码的设计过程中，LU分解可以不需要额外的存储空间，即可把 $U$ 的非零部分存储到 $A$ 的上三角部分，把 $L$ 的非零部分存储到 $A$ 的下三角部分。

代码详见附录。

1.2 Crout(克劳特)分解

将 $A$ 分解式 $A=LU$ 中 $U(u_{ii}\neq 0,i=1:n)$ 进一步分解为

$\boldsymbol{U}=\left(\begin{array}{llll}
\boldsymbol{u}_{11} & & & \\
& \boldsymbol{u}_{22} & & \\
& & \ddots & \\
& & & \boldsymbol{u}_{n n}
\end{array}\right)\left(\begin{array}{cccc}
\mathbf{1} & u_{12} / u_{11} & \cdots & u_{1 n} / u_{11} \\
& \mathbf{1} & \cdots & u_{2 n} / u_{22} \\
& & \ddots & \vdots \\
& & & \mathbf{1}
\end{array}\right)\triangleq D \bar{U}$

则 $A=LD\bar{U}=(LD)\bar{U}\triangleq \bar{L} \bar{U}$，简记为 $A=LU$ ，其中 $L$ 是下三角矩阵，$U$ 是单位上三角矩阵。

上述分解也可记为 $A=LDU$，称为 $LDU$ 分解法。其中 $L$ 是单位下三角矩阵，$U$ 是单位上三角矩阵，$D$是对角矩阵。

我们对对称矩阵有下述定理：

若 $A\in R^{n*n}$ 是对称矩阵，且 $A$ 的顺序主子式 $D_i\neq0(i=1:n)$，则 $A$ 可唯一分解为 $A=LDL^T$，其中 $L$ 为单位下三角矩阵，$D$ 为对角矩阵。

证明：

因为 $A$ 的各阶顺序主子式都不等于零，则有 $A$ 可唯一分解为

$A=\left[\begin{array}{cccc}
1 & & & \\
l_{21} & 1 & & \\
\vdots & \vdots & \ddots & \\
l_{n 1} & l_{n 2} & \cdots & 1
\end{array}\right]\left[\begin{array}{cccc}
u_{11} & u_{12} & \cdots & u_{1 n} \\
& u_{22} & \cdots & u_{2 n} \\
& & \ddots & \vdots \\
& & & u_{n n}
\end{array}\right] \text { 且 } u_{i i} \neq 0(i=1,2, \cdots, n)$

因为 $U_{ii}\neq 0(i=1,2,…,n)$，所以 $U$ 可进一步分解为 $U=\left[\begin{array}{llll}
u_{11} & & & \\
& u_{22} & & \\
& & \ddots & \\
& & & u_{n n}
\end{array}\right]\left[\begin{array}{cccc}
1 & \frac{u_{12}}{u_{11}} & \cdots & \frac{u_{1 n}}{u_{11}} \\
& 1 & \cdots & \frac{u_{2 n}}{u_{22}} \\
& & \ddots & \vdots \\
& & & 1
\end{array}\right]=D U_{1}$

其中 $D$ 为对角矩阵，$U_1$为上三角阵。故 $A=LDU_1=L(DU_1)$。

由 $A$ 是对称矩阵，则 $A=A^{T}=U_{1}^{T} D^{T} L^{T}=U_{1}^{T} D L^{T}=U_{1}^{T}\left(D L^{T}\right)$

又有 $LU$ 分解唯一，则 $L=U_1^{T}$，故 $A=LDL^T$

1.3 Cholesky分解法

1.3.1 概述

Cholesky分解法又叫平方根法，是求解对称正定线性方程组最常用的方法之一。对于一般矩阵，为了消除LU分解的局限性和误差的过分积累，采用了选主元的方法，但对于对称正定矩阵而言，选主元是不必要的。

有以下定理：若 $A\in R^{nn}$ 对称正定，则存在一个对角元为正数的下三角矩阵 $L\in R^{nn}$，使得 $A=LL^{T}$ 成立。

对称：$A=A^{T}$

正定：$X^TAX>0(x\neq 0)$

假设现在要求解线性方程组 $AX=B$，其中 $A$ 为对称正定矩阵，那么 $X$ 可通过下面步骤求解：

求 $A$ 的Cholesky分解，得到 $A=LL^T$
求解 $LY=B$，得到 $Y$
求解 $L^TX=Y$，得到 $X$

现在的关键问题是 $A$ 对进行Cholesky分解。

1.3.2 求矩阵 $L$ 的第一列元素

假设

$L=\left(\begin{array}{cccc}
l_{11} & 0 & \cdots & 0 \\
l_{21} & l_{22} & \cdots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
l_{n 1} & l_{n 2} & \cdots & l_{n n}
\end{array}\right) \quad L^{T}=\left(\begin{array}{cccc}
l_{11} & l_{21} & \cdots & l_{n 1} \\
0 & l_{22} & \cdots & l_{n 2} \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & l_{n n}
\end{array}\right)$

通过比较 $A = LL^T$ 比较两边的关系，首先由 $a_11=l_{11}^2$，得到 $l_{11}=\sqrt{a_{11}}$，再由 $a_{i1}=l_{11}l_{i1}$，得到

$l_{i1}=\frac{a_{i1}}{l_{11}}(i=2,3,…,n)$

这样就得到了矩阵 $L$ 的第一列元素。

1.3.3 求矩阵 $L$ 的第 $k$ 列元素

假定已经算出了 $L$ 的前 $k-1$ 列元素，通过$a_{k k}=\sum_{i=1}^{k} l_{k i}^{2}$，可以得到$l_{k k}=\sqrt{a_{k k}-\sum_{i=1}^{k-1} l_{k i}^{2}}$。

进一步再由$a_{i k}=\sum_{j=1}^{k-1} l_{i j} l_{k j}+l_{i k} l_{k k} \quad(i=k+1, \ldots, n)$，最终得到：

$l_{i k}=\frac{a_{i k}-\sum_{j=1}^{k-1} l_{i j} l_{k j}}{l_{k k}} \quad(i=k+1, \ldots, n)$

这样便通过 $L$ 的前 $k-1$ 列求出了第 $k$ 列，一直递推下去即可求出 $L$ ，这种方法称为Cholesky分解法。

代码详见附录。

1.3.4 改进版本

用上述的方法进行LU分解时需要进行开方运算，这有可能损失精度和增加运算量，为了避免开方，Cholesky分解有个改进的版本。

将对称正定矩阵通过分解成 $A=LDL^{T}$ ，其中 $L$ 是单位下三角矩阵，$D$是对角均为正数的对角矩阵。把这一分解叫做 $LDL^T$分解，是Cholesky分解的变形。对应两边的元素，很容易得到：

$a_{i j}=\sum_{k=1}^{j-1} l_{i k} d_{k} l_{j k}+l_{i j} d_{j} \quad(1 \leq j \leq i \leq n)$

由此可以确定计算 $l_{ij}$ 和 $d_j$ 的公式如下：

$u_{k}=d_{k} l_{j k} (k=1,2, \ldots, j-1)$
$d_{j}=a_{j j}-\sum_{k=1}^{j-1} l_{j k} u_{k}$
$l_{i j}=\frac{a_{i j}-\sum_{k=1}^{j-1} l_{i k} u_{k}}{d_{j}} \quad(i=j+1, \ldots, n)$

在实际计算时，是将 $L$ 的严格下三角元素存储在的对应位置上，而将 $D$ 的对角元存储在 $A$ 的对应对角位置上。

类似地，该方法求解线性方程组 $AX=B$ 的解的步骤如下：

对矩阵进行分解得到
求解 $LY=B$，得到 $Y$
求解 $DL^TX=Y$，得到 $X$

代码详见附录。

高斯消去法的现代商业实现是以LU分解为基础的。

二、可逆矩阵的逆

给出方案计算可逆矩阵的逆。

2.1 待定系数法

设 $A$ 是一个 $n$ 阶方阵，若存在另一个 $n$ 阶方阵 $B$，使得 $AB=BA=E$，则称方阵 $A$ 可逆，并称方阵 $B$ 是 $A$ 的逆矩阵。

我们可以根据定义，用待定系数法求逆矩阵：

矩阵$A=\left(\begin{array}{ll}
1 & 2 \\
-1 & -3
\end{array}\right)$，假设所求的逆矩阵为$\left(\begin{array}{ll}
a & b \\
c & d
\end{array}\right)$，则有：$\left(\begin{array}{ll}
1 & 2 \\
-1 & -3
\end{array}\right)\left(\begin{array}{ll}
a+2c & b+2d \\
-a-3c & -b-3d
\end{array}\right)=\left(\begin{array}{ll}
1 & 0 \\
0 & -1
\end{array}\right)$

得到方程组：

$\begin{cases}
a + 2c = 1\\b + 2d = 0\-a - 3c = 0\-b - 3d = 1\end{cases}$

解得

$\begin{cases}
a = 3\\b = 2\\c = -1\\d = -1\end{cases}$

2.2 伴随矩阵法

设矩阵，将矩阵的元素所在的第 $i$ 行第 $j$ 列元素划去后，剩余的各元素按原来的排列顺序组成的 $n-1$ 阶矩阵所确定的行列式称为元素的余子式，记为，称

为元素的代数余子式。

方阵的各元素的代数余子式所构成的如下矩阵

$A^*$ 称为 $A$ 的伴随矩阵。

伴随矩阵法求逆矩阵的方法为：若 $|A|\neq 0$，则 $A^{-1}=\frac{A^*}{|A|}$

如，求 $A=\left(\begin{array}{ll}
a & b \\
c & d
\end{array}\right)$的逆矩阵，有

$\begin{array}{l}
A^{-1}=\frac{1}{a d-b c}\left(\begin{array}{cc}
d & -b \\
-c & a
\end{array}\right) \\
=\left(\begin{array}{cc}
\frac{d}{a d-b c} & -\frac{b}{a d-b c} \\
-\frac{c}{a d-b c} & \frac{a}{a d-b c}
\end{array}\right)
\end{array}$

引入伴随矩阵更多是为了说明逆矩阵的存在性，除了二阶矩阵，一般不用其求具体矩阵的逆矩阵。

代码设计如下：

typedef vector<double> vec;
typedef vector<vec> mat;

mat cutoff(mat A, int i, int j) {  //切割，划去第1行第i列
	mat B(A.size() - 1, vec(A.size() - 1));
	for(int c = 0; c < B.size(); c++)
		for(int r = 0; r < B.size(); r++)
			B[c][r] = A[c + (c >= i)][r + (r >= j)];
	return B;
}

double det(mat A) {
	if(A.size() == 1)
		return A[0][0];  //当A为一阶矩阵时，直接返回A中唯一的元素
	double ans = 0;
	for(int j = 0; j < A.size(); j++)
		ans += A[0][j] * det(cutoff(A, 0, j)) * (j % 2 ? -1 : 1);
	return ans;
}

mat company_mat(mat A) {
	mat B(A.size(), vec(A.size()));
	for(int i = 0; i < B.size(); i++)
		for(int j = 0; j < B.size(); j++)
			B[j][i] = det(cutoff(A, i, j)) * ((i + j) % 2 ? -1 : 1);
	return B;
}

void output(mat A) {
	cout << "......\n";
	for(int i = 0; i < A.size(); i++) {
		for(int j = 0; j < A[0].size(); j++)
			printf("%.2lf ", A[i][j]);
		cout << '\n';
	}
	cout << "......\n";
}

mat num_mul(mat A, double num) {
	mat B(A.size(), vec(A[0].size()));
	for(int i = 0; i < B.size(); i++)
		for(int j = 0; j < B[0].size(); j++)
			B[i][j] = A[i][j] * num;
	return B;
}

2.3 初等变换法

我们有以下结论：对于一个矩阵的初等行变换，有三种：

交换两行；
将某一行的所有元素乘以一个非零实数 $k$；
将某一行 $j$，加上某一行 $i(i≠j)$ 乘以一个非零实数 $k$，即$A_j=A_j+A_i∗k$。

可以发现的是，每种变换其实都可以等价于乘以某个矩阵，事实上称其为初等矩阵。则我们可以通过初等行变换求出可逆矩阵的逆：

设 $A$ 为可逆矩阵，则 $\left(\begin{array}{ll}
A & I
\end{array}\right) \stackrel{\text { 初等行变换 }}{\longrightarrow}\left(I \quad A^{-1}\right)$

例如，我们求$A=\left(\begin{array}{ccccc}
1 & 1 & \cdots & \cdots & 1 \\
1 & 0 & 1 & \cdots & 1 \\
& & \ddots & & \\
1 & & \cdots & 0 & 1 \\
1 & & \cdots & 1 & 0
\end{array}\right)$的逆，可以进行以下的初等行变换：

$\left(\begin{array}{ccccccccc}
1 & 1 & \cdots & \cdots & 1 & 1 & & & \\
1 & 0 & 1 & \cdots & 1 & & 1 & & \\
1 & 1 & 0 & 1 & 1 & & & \cdots & \\
& & & & & & & & \\
1 & 1 & \cdots & 1 & 0 & & & & 1
\end{array}\right) \rightarrow$

$\left(\begin{array}{ccccccccc}
1 & 1 & \cdots & \cdots & 1 & 1 & & & \\
0 & -1 & 0 & \cdots & 0 & -1 & 1 & & \\
0 & 0 & -1 & 0 & 0 & -1 & & \cdots & \\
& & & & & & & & \\
0 & 0 & \cdots & 0 & -1 & -1 & & & 1
\end{array}\right) \rightarrow$

$\left(\begin{array}{cccccccccc}
1 & 0 & \cdots & \cdots & 0 & -(n-2) & 1 & \cdots & \cdots & 1 \\
0 & 1 & 0 & \cdots & 0 & 1 & -1 & & & \\
0 & 0 & 1 & 0 & 0 & 1 & & \cdots & & \\
& & & & & & & & & \\
0 & 0 & \cdots & 0 & 1 & 1 & & & & -1
\end{array}\right)$

故 $A^{-1}=\left(\begin{array}{ccccc}
-(n-2) & 1 & \cdots & \cdots & 1 \\
1 & -1 & & & \\
\vdots & & -1 & & \\
1 & & & & \\
1 & & & \cdots & \\
1 & & & & -1
\end{array}\right)$

初等行变换求逆矩阵的代码详见附录。

运行结果如下：

Input：

—-行列数：3

输入行列式：
1 0 0
2 1 0
5 4 1

Output：

|A|=1

(A|E)=
| 1 0 0 | 1 0 0 |
| 2 1 0 | 0 1 0 |
| 5 4 1 | 0 0 1 |

R2-2R1:
| 1 0 0 | 1 0 0 |
| 0 1 0 | -2 1 0 |
| 5 4 1 | 0 0 1 |

R3-5R1:
| 1 0 0 | 1 0 0 |
| 0 1 0 | -2 1 0 |
| 0 4 1 | -5 0 1 |

R3-4R2:
| 1 0 0 | 1 0 0 |
| 0 1 0 | -2 1 0 |
| 0 0 1 | 3 -4 1 |

Result:
| 1 0 0 |
| -2 1 0 |
| 3 -4 1 |

用初等行变换法求逆矩阵具有普适性。

附：源代码

Doolittle(杜利特尔)直接分解法

#include <stdio.h>
#include <stdlib.h>

double sumU(double L[4][4] ,double U[4][4], int i, int j ){
    double sU = 0.0;
    for (int k = 1; k <= i-1 ; k++)
    {
        sU += L[i-1][k-1] * U[k-1][j-1];
    }

    return sU;
} //计算求和1

double sumL(double L[4][4] ,double U[4][4], int i, int j ){
    double sL = 0.0;
    for (int k = 0; k <= j-1; k++)
    {
        sL += L[i-1][k-1] * U[k-1][j-1];
    }

    return sL;

} //计算求和2

double sumY(double L[4][4] ,double y[4],int i){
    double sY=0.0;
    for (int k = 1; k <= i - 1; k++)
    {
        sY += L[i-1][k-1] * y[k-1];
    }
    return sY;
} //计算求和3

double sumX(double U[4][4] ,double x[4],int i ,int m){
    double sX = 0.0;
    for (int k = i+1; k <= m; k++)
    {
        sX += U[i-1][k-1] * x[k-1];
    }
    return sX;
} //计算求和4

int main(){

    double a[4][4] = { {1,2,3,1,},
                    {1,4,1,-1,},
                    {1,-1,-2,3,},
                    {1,3,-1,2}};//将系数存入二维数组
    double L[4][4] = {0};
    double U[4][4] = {0};//初始化部分
    double b[4] = {8,8,12,19};
    int n = 4;//n阶
    //输出[Ab]
    printf("[A]:\n");
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= n; j++)
        {
            printf("%f\t", a[i-1][j-1]);
        }
        printf("\n");
    }

    //计算L,U
    for (int i = 1; i <= n; i++)
    {
        L[i-1][i-1] = 1;//对角线元素为1
        for (int j = i; j <= n; j++)
        {
            //由于数组下标从0开始 所以i-1,j-1
            U[i-1][j-1] = a[i-1][j-1] - sumU(L,U,i,j);

            if(j+1 <= n) L[j][i-1] = (a[j][i-1] - sumL(L,U,j+1,i))/U[i-1][i-1];//i变j+1，j变i 
        }

    }

    //输出U
    printf("U:\n");
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= n; j++)
        {
            printf("%f\t",U[i-1][j-1]);
        }
        printf("\n");
    }
    
    //输出L
    printf("L:\n");
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= n; j++)
        {
            printf("%f\t",L[i-1][j-1]);
        }
        printf("\n");
    }

    //由Ly=b 求y
    double y[4] = {0.0};
    y[0] = b[0];//y(1) = b(1);

    for (int i = 2; i <= n; i++)
    {
        y[i-1] = b[i-1] - sumY(L,y,i);
    }

    //由 Ux=y 求x
    double x[4] = {0.0};

    for (int i = n; i >= 1; i--)
    {
        x[i-1] =( y[i-1] - sumX(U,x,i,n))/ U[i-1][i-1];
    }

    //输出y
    printf("y:\n");
    for (int i = 0; i < n; i++)
    {
        printf("%f\n",y[i]);
    }
    printf("\n");
    //输出x
    printf("x:\n");
    for (int i = 0; i < n; i++)
    {
        printf("%f\n",x[i]);
    }
    printf("\n");
    system("pause");
    return 0;
}

Cholesky分解法

#include <iostream>
#include <string.h>
#include <stdio.h>
#include <vector>
#include <math.h>
 
using namespace std;
const int N = 1005;
typedef double Type;
 
Type A[N][N], L[N][N];
 
/** 分解A得到A = L * L^T */
void Cholesky(Type A[][N], Type L[][N], int n)
{
    for(int k = 0; k < n; k++)
    {
        Type sum = 0;
        for(int i = 0; i < k; i++)
            sum += L[k][i] * L[k][i];
        sum = A[k][k] - sum;
        L[k][k] = sqrt(sum > 0 ? sum : 0);
        for(int i = k + 1; i < n; i++)
        {
            sum = 0;
            for(int j = 0; j < k; j++)
                sum += L[i][j] * L[k][j];
            L[i][k] = (A[i][k] - sum) / L[k][k];
        }
        for(int j = 0; j < k; j++)
            L[j][k] = 0;
    }
}
 
/** 回带过程 */
vector<Type> Solve(Type L[][N], vector<Type> X, int n)
{
    /** LY = B  => Y */
    for(int k = 0; k < n; k++)
    {
        for(int i = 0; i < k; i++)
            X[k] -= X[i] * L[k][i];
        X[k] /= L[k][k];
    }
    /** L^TX = Y => X */
    for(int k = n - 1; k >= 0; k--)
    {
        for(int i = k + 1; i < n; i++)
            X[k] -= X[i] * L[i][k];
        X[k] /= L[k][k];
    }
    return X;
}
 
void Print(Type L[][N], const vector<Type> B, int n)
{
    for(int i = 0; i < n; i++)
    {
        for(int j = 0; j < n; j++)
            cout<<L[i][j]<<" ";
        cout<<endl;
    }
    cout<<endl;
    vector<Type> X = Solve(L, B, n);
    vector<Type>::iterator it;
    for(it = X.begin(); it != X.end(); it++)
        cout<<*it<<" ";
    cout<<endl;
}
 
int main()
{
    int n;
    cin>>n;
    memset(L, 0, sizeof(L));
    for(int i = 0; i < n; i++)
    {
        for(int j = 0; j < n; j++)
            cin>>A[i][j];
    }
    vector<Type> B;
    for(int i = 0; i < n; i++)
    {
        Type y;
        cin>>y;
        B.push_back(y);
    }
    Cholesky(A, L, n);
    Print(L, B, n);
    return 0;
}

改进版本：

#include <iostream>
#include <string.h>
#include <stdio.h>
#include <vector>
#include <math.h>
 
using namespace std;
const int N = 1005;
typedef double Type;
 
Type A[N][N], L[N][N], D[N][N];
 
/** 分解A得到A = LDL^T */
void Cholesky(Type A[][N], Type L[][N], Type D[][N], int n)
{
    for(int k = 0; k < n; k++)
    {
        for(int i = 0; i < k; i++)
            A[k][k] -= A[i][i] * A[k][i] * A[k][i];
        for(int j = k + 1; j < n; j++)
        {
            for(int i = 0; i < k; i++)
                A[j][k] -= A[j][i] * A[i][i] * A[k][i];
            A[j][k] /= A[k][k];
        }
    }
    memset(L, 0, sizeof(L));
    memset(D, 0, sizeof(D));
    for(int i = 0; i < n; i++)
    {
        D[i][i] = A[i][i];
        L[i][i] = 1;
    }
    for(int i = 0; i < n; i++)
    {
        for(int j = 0; j < i; j++)
            L[i][j] = A[i][j];
    }
}
 
void Transposition(Type L[][N], int n)
{
    for(int i = 0; i < n; i++)
    {
        for(int j = 0; j < i; j++)
            swap(L[i][j], L[j][i]);
    }
}
 
void Multi(Type A[][N], Type B[][N], int n)
{
    Type **C = new Type*[n];
    for(int i = 0; i < n; i++)
        C[i] = new Type[n];
    for(int i = 0; i < n; i++)
    {
        for(int j = 0; j < n; j++)
        {
            C[i][j] = 0;
            for(int k = 0; k < n; k++)
                C[i][j] += A[i][k] * B[k][j];
        }
    }
    for(int i = 0; i < n; i++)
    {
        for(int j = 0; j < n; j++)
            B[i][j] = C[i][j];
    }
    for(int i = 0; i < n; i++)
    {
        delete[] C[i];
        C[i] = NULL;
    }
    delete C;
    C = NULL;
}
 
/** 回带过程 */
vector<Type> Solve(Type L[][N], Type D[][N], vector<Type> X, int n)
{
    /** LY = B  => Y */
    for(int k = 0; k < n; k++)
    {
        for(int i = 0; i < k; i++)
            X[k] -= X[i] * L[k][i];
        X[k] /= L[k][k];
    }
    /** DL^TX = Y => X */
    Transposition(L, n);
    Multi(D, L, n);
    for(int k = n - 1; k >= 0; k--)
    {
        for(int i = k + 1; i < n; i++)
            X[k] -= X[i] * L[k][i];
        X[k] /= L[k][k];
    }
    return X;
}
 
void Print(Type L[][N], Type D[][N], const vector<Type> B, int n)
{
    for(int i = 0; i < n; i++)
    {
        for(int j = 0; j < n; j++)
            cout<<L[i][j]<<" ";
        cout<<endl;
    }
    cout<<endl;
    vector<Type> X = Solve(L, D, B, n);
    vector<Type>::iterator it;
    for(it = X.begin(); it != X.end(); it++)
        cout<<*it<<" ";
    cout<<endl;
}
 
int main()
{
    int n;
    cin>>n;
    memset(L, 0, sizeof(L));
    for(int i = 0; i < n; i++)
    {
        for(int j = 0; j < n; j++)
            cin>>A[i][j];
    }
    vector<Type> B;
    for(int i = 0; i < n; i++)
    {
        Type y;
        cin>>y;
        B.push_back(y);
    }
    Cholesky(A, L, D, n);
    Print(L, D, B, n);
    return 0;
}

伴随矩阵法求逆矩阵

#include<iostream>
#include<vector>
using namespace std;
typedef vector<double> vec;
typedef vector<vec> mat;

mat cutoff(mat A, int i, int j) {  //切割，划去第1行第i列
	mat B(A.size() - 1, vec(A.size() - 1));
	for(int c = 0; c < B.size(); c++)
		for(int r = 0; r < B.size(); r++)
			B[c][r] = A[c + (c >= i)][r + (r >= j)];
	return B;
}

double det(mat A) {
	if(A.size() == 1)
		return A[0][0];  //当A为一阶矩阵时，直接返回A中唯一的元素
	double ans = 0;
	for(int j = 0; j < A.size(); j++)
		ans += A[0][j] * det(cutoff(A, 0, j)) * (j % 2 ? -1 : 1);
	return ans;
}

mat company_mat(mat A) {
	mat B(A.size(), vec(A.size()));
	for(int i = 0; i < B.size(); i++)
		for(int j = 0; j < B.size(); j++)
			B[j][i] = det(cutoff(A, i, j)) * ((i + j) % 2 ? -1 : 1);
	return B;
}

void output(mat A) {
	cout << "......\n";
	for(int i = 0; i < A.size(); i++) {
		for(int j = 0; j < A[0].size(); j++)
			printf("%.2lf ", A[i][j]);
		cout << '\n';
	}
	cout << "......\n";
}

mat num_mul(mat A, double num) {
	mat B(A.size(), vec(A[0].size()));
	for(int i = 0; i < B.size(); i++)
		for(int j = 0; j < B[0].size(); j++)
			B[i][j] = A[i][j] * num;
	return B;
}

int main() {
	int n;
	scanf("%d", &n);  //输入阶数
	if(n == 0)
		return 0;
	mat A(n, vec(n));
	for(int i = 0; i < n; i++)
		for(int j = 0; j < n; j++)
			scanf("%lf", &A[i][j]);  //输入A各行各列的元素
	mat B = num_mul(company_mat(A), 1 / det(A));
	output(B);
	return 0;
}

初等变换法求逆矩阵

#include<iostream>
#include<iomanip>
using namespace std;

//左下角变换0 若对角不为1元素下方元素为1交换两行
//对角变1
//右上角变换0
void LD_triangle(float temp[6][12],int n);
void RU_triangle(float temp[6][12],int n);
void Aii_Cto_1(float temp[6][12],int n);
void Display(float A[6][12],int m,int n);
int Find(float temp[6][12],int i,int n);
void Swap(float temp[6][12],int i,int j,int n);

class Matrix{
public:
    Matrix(){
        n=9;
        for(int i=0;i<6;i++)
            for(int j=0;j<12;j++)
                A[i][j]=0;
        Det_A=0;
    }
    void Conversion();
    void Input();
    bool Cal_DetA();
    friend void Save_To_Result(float temp[6][12],Matrix &D);
    void Cheak_IsSolvable();
    void Out_Result();
private:
    int n;                  //阶
    float A[6][12];         //矩阵
    float result[6][6];     //逆矩阵结果
    float Det_A;            //|A|值 ：是否存在逆矩阵
};


int main(){
    cout<<"\n\t\t-------求逆矩阵（初等变换法）-------"<<endl<<endl;
    while(1){
        Matrix D;
        D.Input();
        D.Cheak_IsSolvable();   //可解
        D.Conversion();         //变换
        D.Out_Result();         //输出
    }
    return 1;
}

void Matrix::Input(){
    cout<<"\n---行列数：";
    cin>>n;
    cout<<endl<<"输入行列式："<<endl;
    for(int i=0;i<n;i++)
        for(int j=0;j<n;j++)
            cin>>A[i][j];
    int j=0;
    for(i=n;i<2*n;i++){
        A[j][i]=1;
        j++;
    }
}
void Matrix::Cheak_IsSolvable(){
    while(1){
        if(Cal_DetA()){
        cout<<"\n|A|="<<Det_A<<endl<<endl;
            cout<<"(A|E)="<<endl;
            Display(A,n,2*n);
            break;
        }
        else{
            cout<<"此矩阵的行列式为0，无解"<<endl;
            Input();
        } 
    }
}
void Matrix::Conversion(){
    float temp[6][12];
    for(int i=0;i<n;i++)//替身
        for(int j=0;j<2*n;j++)
            temp[i][j]=A[i][j];
    LD_triangle(temp,n);//左下角变换0
    Aii_Cto_1(temp,n);   //对角变1
    RU_triangle(temp,n);//右上角变换
    Save_To_Result(temp,*this);
}
void LD_triangle(float temp[6][12],int n){
    for(int i=0;i<n-1;i++){
        if(temp[i][i]){//对角线元素不为0
            if(temp[i][i]!=1.0)
                if(int j=Find(temp,i,n)) Swap(temp,i,j,n);
            for(int m=i+1;m<n;m++){
                if(temp[m][i]){
                    float t=-(temp[m][i])/temp[i][i];
                    for(int p=0;p<2*n;p++){//R(m)+tRi
                        temp[m][p]=temp[m][p]+t*temp[i][p];
                    }
                    if(t>0)
                        cout<<"R"<<m+1<<"+"<<t<<"R"<<i+1<<":"<<endl;
                    else
                        cout<<"R"<<m+1<<t<<"R"<<i+1<<":"<<endl;
                    Display(temp,n,2*n);
                }
                else continue;
            }
        }

        else {//若对角线元素为0
            int m;          for(m=i+1;m<n;m++){//
                if(temp[m][i]){//使对角线元素非0
                    for(int p=0;p<n;p++)//Ri+Rm
                        temp[i][p]=temp[m][p]+temp[i][p];
                    break;
                }
                else continue;
            }
            if(m==n){   //可逆矩阵 不会出现此情况（对角元素为零，且此元素以下全为零）
                //此情况 矩阵 行列式值为0 
            }
            cout<<"R"<<i+1<<"+"<<"R"<<m+1<<endl;
            Display(temp,n,2*n);
            i--;
        }
    }
}
int Find(float temp[6][12],int i,int n){
    for(int m=i+1;m<n;m++)
        if(temp[m][i]==1.0)
            return m;
    return 0;
}
void Swap(float temp[6][12],int i,int j,int n){
    cout<<"R"<<i+1<<"<-->R"<<j+1<<endl;
    for(int m=0;m<2*n;m++){
        temp[i][m]+=temp[j][m];
        temp[j][m]=temp[i][m]-temp[j][m];
        temp[i][m]-=temp[j][m];
    }
    Display(temp,n,2*n);
}
void Aii_Cto_1(float temp[6][12],int n){
    for(int i=0;i<n;i++){
        if(temp[i][i]!=1.0){
            float t=1.0/temp[i][i];
            cout<<"R"<<i+1<<"/"<<temp[i][i]<<endl;
            for(int p=0;p<2*n;p++){//R(m)+tRi
                temp[i][p]*=t;
            }
        Display(temp,n,2*n);
        }
    }
}
void RU_triangle(float temp[6][12],int n){
    for(int i=n-1;i>0;i--){
        for(int m=i-1;m>=0;m--){
            if(temp[m][i]){
                float t=-(temp[m][i])/(temp[i][i]);
                for(int p=i;p<2*n;p++){ //R(m)+tempRi
                    temp[m][p]=temp[m][p]+t*temp[i][p];
                }
                if(t>0)
                    cout<<"R"<<m+1<<"+"<<t<<"R"<<i+1<<":"<<endl;
                else
                    cout<<"R"<<m+1<<t<<"R"<<i+1<<":"<<endl;
                Display(temp,n,2*n);
            }
            else continue;
        }
    }
}
void Display(float A[6][12],int m,int n){
    for(int i=0;i<m;i++){
        cout<<"|";
        for(int j=0;j<n;j++){
            cout<<setw(8)<<A[i][j];
            if((j+1)%m==0) 
                cout<<"  |";
        }
        cout<<endl;
    }
    cout<<endl;
}
void Save_To_Result(float temp[6][12],Matrix &D){
    for(int i=0;i<D.n;i++)
        for(int j=D.n;j<2*D.n;j++)
            D.result[i][j-D.n]=temp[i][j];
}
bool Matrix::Cal_DetA(){
    float temp[6][6];
    for(int i=0;i<n;i++)
            for(int j=0;j<n;j++)
                temp[i][j]=A[i][j];
    for(i=0;i<n-1;i++){
        if(temp[i][i]){//对角线元素不为0
            for(int m=i+1;m<n;m++){
                if(temp[m][i]){
                    float tem=-(temp[m][i])/temp[i][i];
                    for(int p=0;p<n;p++)//R(m)+tempRi
                        temp[m][p]=temp[m][p]+tem*temp[i][p];
                }
                else continue;
            }
        }
        else {//若对角线元素为0
            int m;
            for(m=i+1;m<n;m++){//
                if(temp[m][i]){//使对角线元素非0
                    for(int p=0;p<n;p++)//Ri+Rm
                        temp[i][p]=temp[m][p]+temp[i][p];
                    break;
                }
                else continue;
            }
            if(m==n){
                Det_A=0;
                return false;
            }
            i--;
        }
    }
    Det_A=temp[0][0];//求对角积
    for(i=1;i<n;i++)
        Det_A=Det_A*temp[i][i];

    if(Det_A) return true;
    else return false;
}
void Matrix::Out_Result(){
    cout<<"Result:"<<endl;
    for(int i=0;i<n;i++){
        cout<<"|";
        for(int j=0;j<n;j++){
            cout<<setw(8)<<result[i][j];
        }
        cout<<"  |"<<endl;
    }
    cout<<endl;
}

ShiQuLiZhi

https://www.qqzzss.top/2022/11/02/homework/algorithm/si-kao-ti-1102-lu-fen-jie-yu-ju-zhen-de-ni/

本博客所有文章除特别声明外，均采用 CC BY 4.0 许可协议。转载请注明来源 ShiQuLiZhi !

算法程序设计

网络安全第二次实验

2022-11-05 信息安全专业课程

信息安全网络安全

算法课外思考题1028(最大子矩阵和与遗产分割)

2022-10-28 作业

算法程序设计

算法课外思考题1102(LU分解与矩阵的逆)

一、矩阵的LU分解

1.1 Doolittle(杜利特尔)直接分解法

1.2 Crout(克劳特)分解

1.3 Cholesky分解法

1.3.1 概述

1.3.2 求矩阵 $L$ 的第一列元素

1.3.3 求矩阵 $L$ 的第 $k$ 列元素

1.3.4 改进版本

二、可逆矩阵的逆

2.1 待定系数法

2.2 伴随矩阵法

2.3 初等变换法

附：源代码

Doolittle(杜利特尔)直接分解法

Cholesky分解法

伴随矩阵法求逆矩阵

初等变换法求逆矩阵