💡Author:信安2002钱泽枢(ShiQuLiZhi)
🚀欢迎访问我的作业合集:https://sxhthreo.github.io/categories/%E4%BD%9C%E4%B8%9A/
一、证明题1
证明堆排序中构建初始堆的时间复杂度为 $O(n)$。
我们知道,我们构建初始堆时,需要进行操作以维护大根堆/小根堆的性质。如在维护小根堆过程中,需要调用以下函数:
void down(int u)
{
int t = u; // t为点、左孩子、右孩子三个点中最小的一个点
if (u * 2 <= cnt && h[u * 2] < h[t]) t = u * 2;
if (u * 2 + 1 <= cnt && h[u * 2 + 1] < h[t]) t = u * 2 + 1;
if (u != t) // 根节点不是最小的
{
// 与最小的点交换
swap(h[u], h[t]);
down(t); // 递归处理
}
}该过程中,除了需要递归调用之外,其余比较等操作花费的运行时间均是 $O(1)$ 的,则该操作的时间代价可以用下面的递归式表示:$T(n)\leq T(\frac{2n}{3})+O(1)$,其中 $O(1)$ 代表其余非递归的操作,由于每个节点的子树数量最多为 $\frac{2}{3}n$,且该最大值仅在最底层恰好半满时取到,如下图所示:
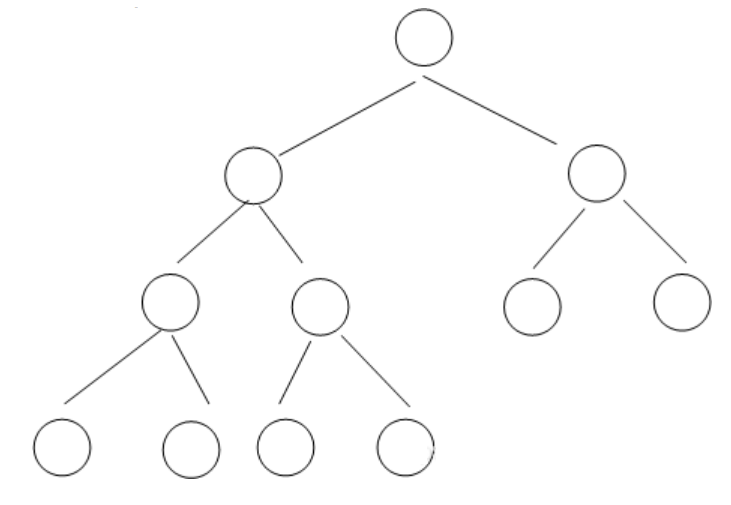
则 $T(\frac{2n}{3})$ 代表子树递归调用的最大值。
简单推导如下:
假设节点的右子树节点个数为 $2^k - 1$ ,那么左子树节点个数为 $2^{k+1} - 1$,总节点个数为 $2^k + 2^{k+1} -1$,左子树占总数的比例为 $\frac{2^{k+1} - 1}{2^k + 2^{k+1} -1}$。
当$k\rightarrow ∞$时,这个比例为 $ \frac23$。
因此可用 $T(n)\leq T(\frac{2n}{3})+O(1)$ 递归式刻画维护小根堆操作的运行时间。根据迭代法可知,运行时间 $T(n)=O(lgn)$,即高为 $h$ 的堆维护小根堆操作的运行时间为 $O(h)$。
又有高度为 $h$ 的堆最多包含结点数 $\lceil n/2^{h+1}\rceil$,则建堆的总代价为 $\sum_{\mathrm{h}=0}^{\lfloor\operatorname{lgn}\rfloor}\left\lceil\frac{\mathrm{n}}{2^{\mathrm{h}+1}}\right\rceil \mathrm{O}(\mathrm{h})=\mathrm{O}\left(\mathrm{n} \sum_{\mathrm{h}=0}^{\lfloor\operatorname{lgn}\rfloor} \frac{\mathrm{h}}{2^{\mathrm{h}}}\right)$
又根据公式 $\sum_{\mathrm{k}=0}^{\infty} \mathrm{kx}^{\mathrm{k}}=\frac{\mathrm{x}}{(1-\mathrm{x})^{2}}$,有 $\sum_{\mathrm{h}=0}^{\infty} \frac{\mathrm{h}}{2^{\mathrm{h}}}=2$,因此有建堆的总代价:
$\mathrm{O}\left(\mathrm{n} \sum_{\mathrm{h}=0}^{\lfloor\operatorname{lgn}\rfloor} \frac{\mathrm{h}}{2^{\mathrm{h}}}\right)=\mathrm{O}\left(\mathrm{n} \sum_{\mathrm{h}=0}^{\infty} \frac{\mathrm{h}}{2^{\mathrm{h}}}\right)=\mathrm{O}(\mathrm{n})$
故堆排序中构建初始堆的时间复杂度为 $O(n)$。
二、证明题2
证明图 $G$ 中顶点 $v_i$ 到顶点 $v_j$ 之间长度为 $k$ 的路径数量等于 $A^k$ 的第 $(i,j)$ 个元素,其中 $A$ 是图 $G$ 的邻接矩阵。
我们采用数学归纳法证明:
当 $k=1$ 时,若 $a_{ij}=1$,说明存在一条边 $<v_i,v_j>$ ,也即从 $v_i$ 到 $v_j$ 存在一条长度为 $1$ 的路径。
假设当 $k=m$ 时有图 $G$ 中顶点 $v_i$ 到顶点 $v_j$ 之间长度为 $k$ 的路径数量等于 $A^k$ 的第 $(i,j)$ 个元素,则当 $k = m+1$ 时:
由 $A^{(m+1)} =A^{(m)}*A$,故 $a_{ij}^{(m+1)}=\sum_{k=1}^n a_{ik}^{(m)}a_{kj}$
- 若 $a_{ik}^{(m)}$ 和 $a_{kj}$ 不都为 $1$,则有$a_{ik}^{(m)} = 0$或 $a_{kj}=0$,即不同时存在从 $v_i$ 到 $v_k$ 长度为 $m$ 的路径和从 $v_k$ 到 $v_j$ 的边,则不存在从 $v_i$ 到 $v_j$ 长度为 $m+1$ 的路径;
- 若 $a_{ik}^{(m)}$ 和 $a_{kj}$ 都等于 $1$,则有$a_{ik}^{(m)}*a_{kj}=1$,即存在从 $v_i$ 到 $v_k$ 长度为 $m$ 的路径和从 $v_k$ 到 $v_j$ 的边,则存在一条从 $v_i$ 到 $v_j$ 长度为 $m+1$ 的路径;
- 若$a_{kj}$ 等于 $1$ 且 $a_{ik}^{(m)}$ 大于 $1$,则有$a_{ik}^{(m)}*a_{kj}=a_{ik}^{(m)}$,即存在 $a_{ik}^{(m)}$ 条从 $v_i$ 到 $v_k$ 长度为 $m$ 的路径和从 $v_k$ 到 $v_j$ 的边,则存在 $a_{ik}^{(m)}$ 条从 $v_i$ 到 $v_j$ 长度为 $m+1$ 的路径。
综上,对一切 $k$,$A^{(n)}$ 的元素 $a_{ij}^{(n)}$ 表示顶点 $v_i$ 到顶点 $v_j$ 之间长度为 $k$ 的不同路径总数。特别地,我们还可得到,对角线上的元素 $a_{ii}^{(n)}$ 表示经过 $v_i$ 的长度为 $n$ 的不同回路条数。
命题得证。

