💡Author:信安2002钱泽枢(ShiQuLiZhi)
🚀欢迎访问我的作业合集:https://sxhthreo.github.io/categories/%E4%BD%9C%E4%B8%9A/
一、题目描述
任务集合 $S$,$\forall i \in S$,$d_i$ 为截止时间,$t_i$ 为加工时间,其中 $d_i,t_i$ 为正整数. 一个调度$f:S\rightarrow N$,$f(i)$ 为任务 $i$ 的开始时间。试设计贪心算法求最大延迟达到最小的调度,即求 $f$ 使得
$\min {f}\left{\max {i \in S}\left{f(i)+t{i}-d{i}\right}\right}$
$\forall i, j \in S, i \neq j, f(i)+t_{i} \leq f(j) \text { or } f(j)+t_{j} \leq f(i)$
并证明你的算法的正确性。
二、算法思路
根据题意,我们可以考虑三种贪心策略,然后我们将通过直观感受排除两种策略,并证明其余一种策略的正确性:
- 根据 $t_i$ 从小到大安排
- 根据 $d_i-t_i$ 从小到大安排
- 根据 $d_i$ 从小到大安排
我们先看策略1,考虑以下场景:
若某个任务的 $t_i$ 很长,且截止时间 $d_i$ 很短,而其他任务 $t_i$ 很短,但 $d_i$ 很长,此时采用策略1,将对 $t_i$ 很长,且截止时间 $d_i$ 很短的任务造成长延迟,故策略1排除;
我们再看策略2,考虑以下场景:
若某个任务的 $d_i$ 很长,且 $t_i$ 很长,但 $d_i-t_i$ 很小,将选择其作为优先调度,而其他任务将造成大量延时, 故策略2排除;
我们考虑策略3的正确性:
定义以下场景为一个逆序:对任务 $i,j$,任务 $i$ 优先于任务 $j$ 调度,但 $d_i>d_j$。
假设存在一个相邻的逆序(任务 $i,j$),交换这两个逆序的任务对其他任务没有影响。
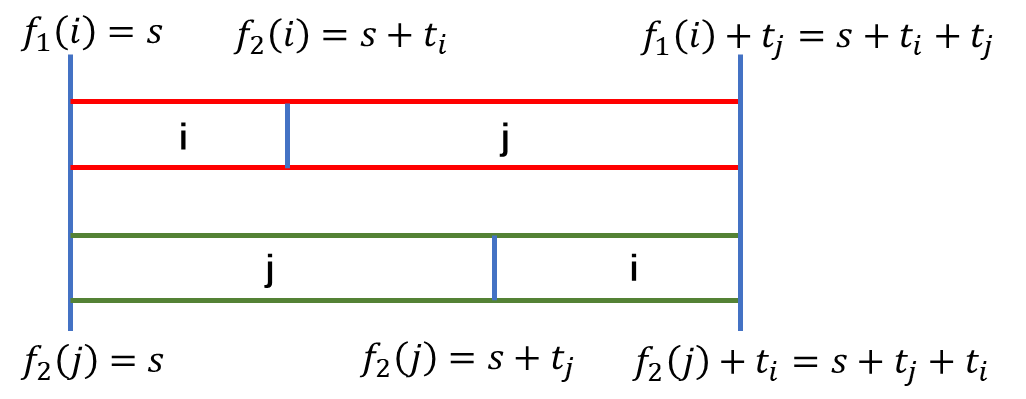
设交换前任务 $i$ 的开始时间为 $s$,则在交换前,$j$ 的任务延迟大于 $i$,延迟时间为 $t_{max1}=max{s+t_i+t_j-d_j,s+t_i-d_i}=s+t_i+t_j-d_j$
交换后,延迟时间的最大值为 $t_{max2}=max{s+t_j+t_i-d_i,s+t_j-d_j}$
由$d_i>d_j$,则$t_{max1}\geq t_{max2}$,则交换后最大延迟减小。
不断交换逆序对,可以使得整个任务的最大延迟不变或减小,当没有逆序对时,即是最优解。
故贪心算法对于本题是正确的。
三、算法设计
struct management
{
int id;
int t; // 加工时间
int d; // 截止时间
bool operator< (const management& W)const
{
return d < W.d;
}
}m[N];
int manage(int n)
{
int maxtime = 0, start = 0; // maxtime是最大延迟时间
sort(m, m + n); // 按照加工时间从小到大排序
cout << "调度顺序是:";
for (int i = 0; i < n; i++)
{
cout << m[i].id + 1 << " ";
maxtime = max(maxtime, start + m[i].t - m[i].d);
start += m[i].t;
}
return maxtime;
}四、运行测试
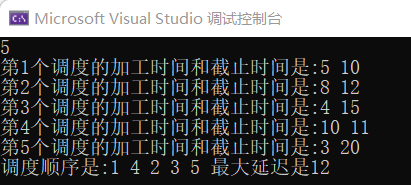
多次测试,算法运行结果均正确,符合题意。
五、总结与讨论
该算法中需要按照截止时间 $d_i$ 为任务进行排序,需要花费的时间复杂度为 $O(nlog;n)$,遍历一遍所有的任务所需的时间复杂度为 $O(n)$,故该算法的时间复杂度为 $O(nlog;n)$。
贪心算法中,选择一种合适的贪心策略是十分必要的,我们可以通过举出特例的方法排除某些策略,并对我们选出的策略进行正确性证明,通常通过数学归纳法、反证法、迭代策略(不断将可行解换成贪心解达到最优)等方法,最终设计出较为简洁且正确的算法。
附:源代码
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1010;
struct management
{
int id;
int t; // 截止时间
int d; // 加工时间
bool operator< (const management& W)const
{
return d < W.d;
}
}m[N];
int manage(int n)
{
int maxtime = 0, start = 0;
sort(m, m + n); // 按照加工时间从小到大排序
cout << "调度顺序是:";
for (int i = 0; i < n; i++)
{
cout << m[i].id + 1 << " ";
maxtime = max(maxtime, start + m[i].t - m[i].d);
start += m[i].t;
}
return maxtime;
}
int main()
{
int n;
cin >> n;
for (int i = 0; i < n; i++)
{
cout << "第" << i + 1 << "个调度的加工时间和截止时间是:";
m[i].id = i;
cin >> m[i].t;
cin >> m[i].d;
}
cout << "最大延迟是" << manage(n) << endl;
return 0;
}
