密码学概述与现代密码算法

Chapter1 密码学概述

1.1 安全服务

• 保密性服务：加密
• 认证鉴别服务：密钥，数字签名
• 访问控制服务：密钥，权限管理
• 完整性服务：加密，数字摘要
• 抗否认性服务：数字签名

1.2 基本攻击类型

• 唯密文攻击
• 已知明文攻击：攻击者知道一些明文密文对
• 选择明文攻击：攻击者可以选择明文密文对
• 针对密钥的攻击：主要是针对公钥密码系统

1.3 密码算法分类

对称密码机制：（DES,AES,SM4,RC4）

• 密钥：加密和解密密钥相同或相互推导出
• 特点：加密速度快,密钥管理复杂

公钥密码机制：（RSA,ECC,SM2,DH）

• 密钥：公钥和私钥不同且很难从公钥推导出私钥
• 特点：密钥管理简单，加密速度慢

密钥管理简单的原因：

只需要将公钥分发给需要加密通信的人，而私钥则仅由接收者持有，不需要在通信中共享私钥，可以避免对密钥进行传输和管理

1.4 古典密码算法

1.4.1 代替密码

• 移位密码
• 仿射密码
  • 加密算法：$y=E_{a,b}(x)=(ax+b)%26$
  • 解密算法：$x = D_{a,b}(y)=(a^{-1}y-a^{-1}b)%26$
• Vignere 密码
  • 将明文消息中的每个字母移动 $k_i$ 位， $k_i$ 为密钥，是长度为 $m$ 的序列 $k = (k_0,k_1,…,k_{m-1})$
  • $y_i = (x_i+k_{i%m}%26)$，密钥空间为 $26^m$
  • 存在周期性弱点。破译方法：重合指数攻击，通过重合指数找到密钥长度，获取移位密码
  • OTP 密码原理相似，是一种多表代替算法，密钥空间为 $26^n$

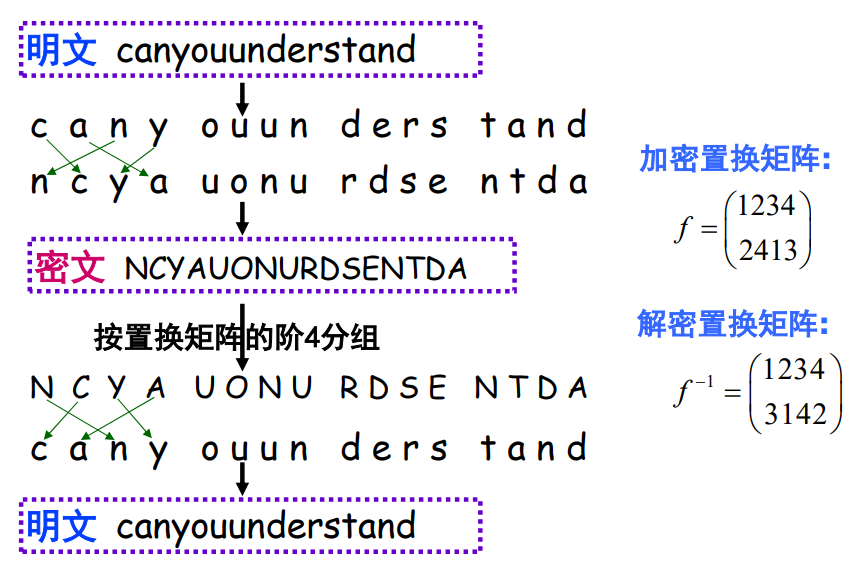
1.4.2 换位密码

• 列换位密码
• 矩阵换位密码
  • 

    image-20230429230434345

1.5 密码学相关数学知识

1.5.1 Euclid算法

x 和 y 为不同时为 $0$ 的整数，则 x 和 y 的最大公因子 (x,y) 是以 ax+by 表示的最小正整数：

计算 $(100,23)$ 的过程：
$100-4×23=8$
$23-2×8=7$
$8-1×7=1$
$7-7×1=0$

image-20230429223555862

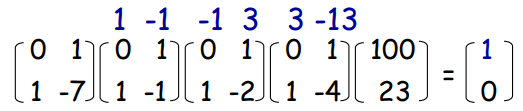
乘法逆元：

$-13×23%100=1$

(*)$23^{-1}%100 = -13 = 87$

$3×100%23=1$

(*)$100^{-1}%23=8^{-1}%23 = 3$

1.5.2 欧拉函数

对于正整数 $n$，与其互素的小于等于 $n$ 的正整数的个数表示为 $\varphi(n)$，有以下定理：

• 若正整数 $m,n$ 满足 $(m,n)=1$，则有 $\varphi(mn) = \varphi(m)\varphi(n)$；特别地，当p为素数时,$\varphi(p)=p-1$
• 正整数 $n=p_{1}^{e_{1}} p_{2}^{e_{2}} \ldots p_{m}^{e_{m}}$ 的欧拉函数 $\varphi(n)$ 值为 $\varphi(n)=\left(p_{1}-1\right) p_{1}^{e_{1}-1}\left(p_{2}-1\right) p_{2}^{e_{2}-1} \ldots\left(p_{m}-1\right) p_{m}^{e_{m}-1}$
• 欧拉定理：对 $n>1$，如果 $(x,n)=1$，则有 $x^{\varphi(n)}\equiv 1 (mod;n)$

应用：由于$2^{\varphi(89)}=1,2^{1000};mod;89=(2^{88})^{11}*2^{32};mod;89=2^{32};mod;89$，可以采用快速指数算法计算答案为 $64$.

快速指数算法

计算 $x^e$，设置三元组 $(X,E,Y)$，其初始值为 $(X,E,Y)=(x,e,1)$

• 若 $E$ 是奇数，则 $Y=X*Y,E=E-1$
• 若 $E$ 为偶数，则 $X=X*X,E=E/2$
• 当 $E=0$ 时，$Y$ 的值即为 $x^e$

image-20230429232000262

Chapter2 现代密码算法

2.1 对称密码算法

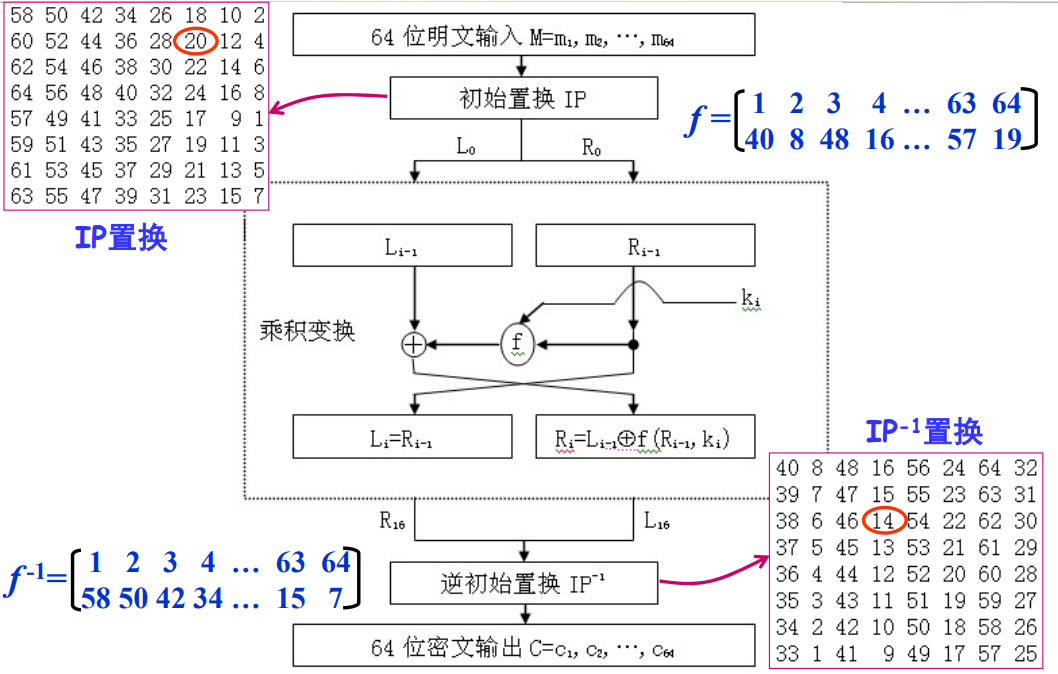
2.1.1 DES算法

DES 算法是一种对称密码算法，分组加密，包括三个步骤：

• 初始置换 $IP$
• $16$ 轮迭代的乘积变换
• 逆初始变换 $IP^{-1}$

image-20230429234131698

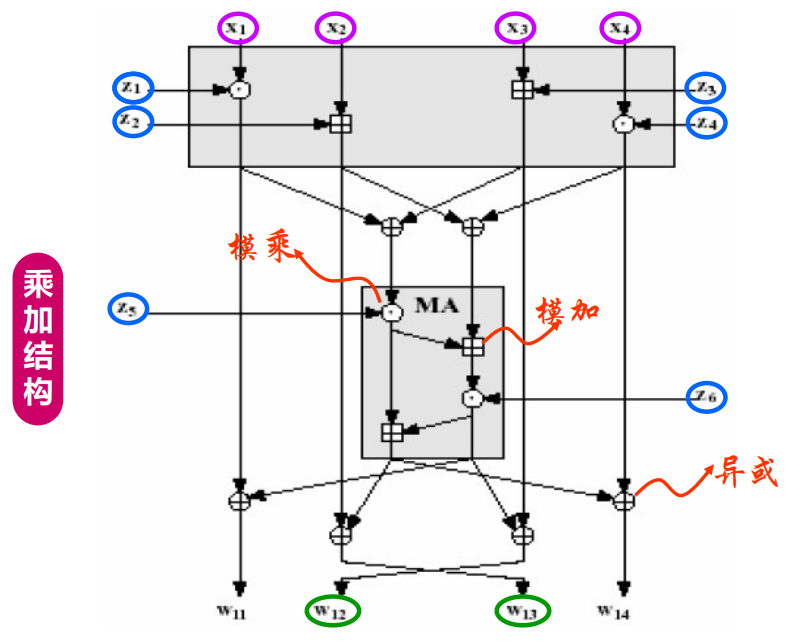
2.1.2 IDEA算法

分组长度为 $64$ 位，分 $4$ 子组进行操作，密钥长度为 $128$ 位，使用异或、模 $216$ 加、模 $216+1$ 乘三个混合运算，在 $16$ 位子分组上进行。

image-20230429234604543

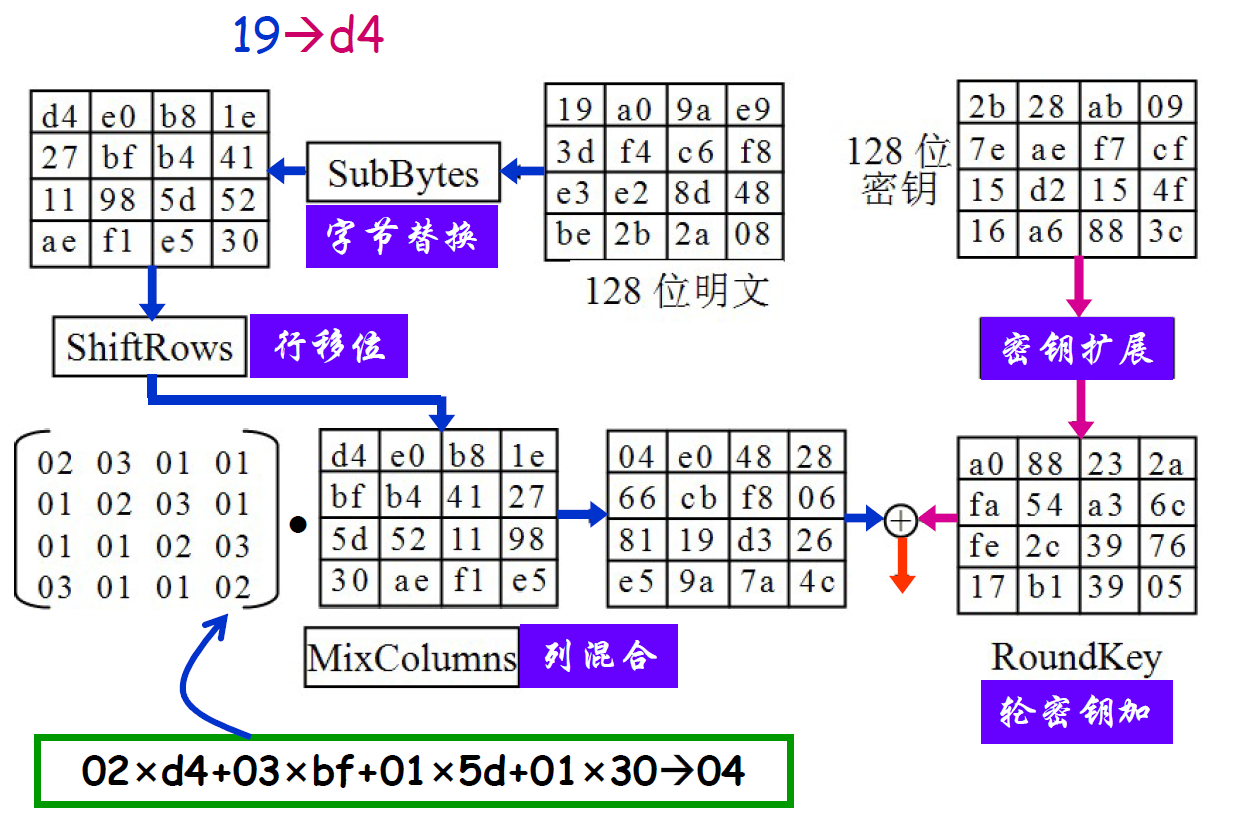
2.1.3 AES算法

128比特的明文分组被分成4×4的字节矩阵

• 字节替换SubBytes：非线性置换,独立作用于状态中的每一个字节

• 行移位运算ShiftRows：字节的循环移位运算,第1行至第4行字节分别向左移动0~3列

• 列混合运算MixColumns：由一个线性变换对状态的每一列进行变换

  none

  02 03 01 01
  01 02 03 01
  01 01 02 03
  03 01 01 02

• 轮密钥加AddRoundKey：与相应的密钥进行异或.

image-20230430000206090

2.2 序列密码算法

• RC4：基于字节流
• LFSR：基于位流

序列密码算法的密钥流不能重复使用，防止重合指数攻击、插入攻击。

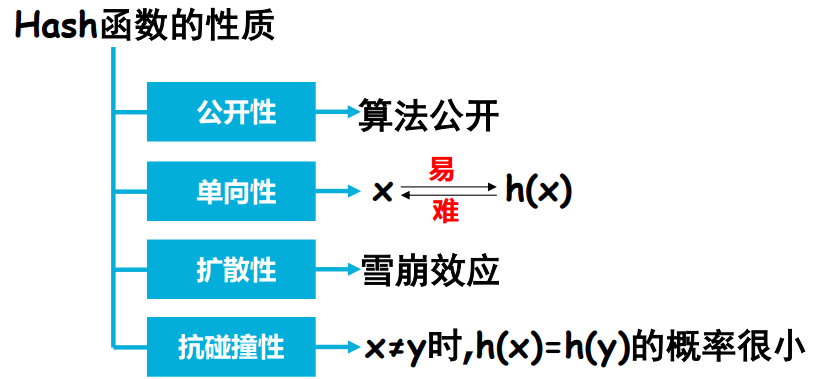
2.3 数字摘要算法

• MD5

• SHA

附加填充比特 $\rightarrow$ 附加长度 $\rightarrow$ 初始化缓冲区 $\rightarrow$ $64(416)$次(MD5)/$80(420)$次(SHA)迭代$\rightarrow$ 输出

image-20230430001522814

image-20230430001706090

2.4 公钥密码算法