LeetCode刷题记录

双指针

盛最多水的容器

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明：你不能倾斜容器。

设两指针 i , j ，指向的水槽板高度分别为 h[i] , h[j] ，此状态下水槽面积为 S(i,j) 。由于可容纳水的高度由两板中的 短板 决定，因此可得如下 面积公式 ：

$S(i,j)=min(h[i],h[j])×(j−i)$

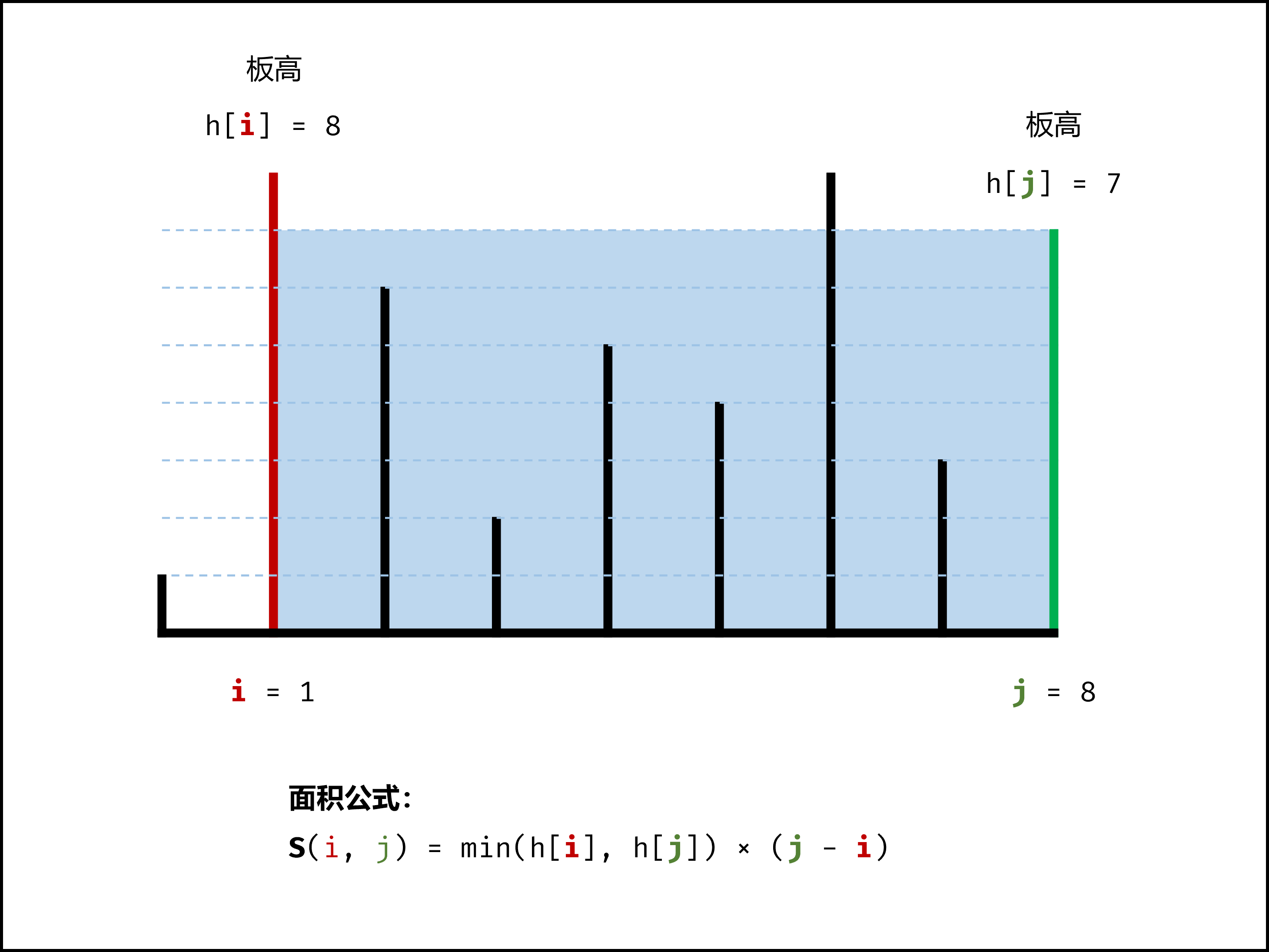
在每个状态下，无论长板或短板向中间收窄一格，都会导致水槽 底边宽度 −1 变短：

• 若向内 移动短板 ，水槽的短板 min(h[i],h[j]) 可能变大，因此下个水槽的面积 可能增大 。
• 若向内 移动长板 ，水槽的短板 min(h[i],h[j]) 不变或变小，因此下个水槽的面积 一定变小 。

因此，初始化双指针分列水槽左右两端，循环每轮将短板向内移动一格，并更新面积最大值，直到两指针相遇时跳出；即可获得最大面积。

class Solution {
    public int maxArea(int[] height) {
        int i = 0, j = height.length - 1, res = 0;
        while(i < j) {
            res = height[i] < height[j] ? 
                Math.max(res, (j - i) * height[i ++]): 
                Math.max(res, (j - i) * height[j --]); 
        }
        return res;
    }
}

三数之和

给你一个整数数组 nums ，判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ，同时还满足 nums[i] + nums[j] + nums[k] == 0 。请

你返回所有和为 0 且不重复的三元组。

注意：答案中不可以包含重复的三元组。

class Solution {
    public List<List<Integer>> threeSum(int[] nums) {
        // 定一个元素, 然后通过双指针来求解
        if(nums == null || nums.length < 3)
            return null;
        Arrays.sort(nums);
        List<List<Integer>> list = new ArrayList<>();
        for(int i = 0; i < nums.length; i ++)
        {
            if(nums[i] > 0)    return list;
            if(i > 0 && nums[i] == nums[i - 1])  continue;   // 重复元素不再考虑
            int l = i + 1; int r = nums.length - 1;
            while(l < r)
            {
                if(nums[i] + nums[l] + nums[r] == 0)
                {
                    list.add(Arrays.asList(nums[i], nums[l], nums[r]));
                    // 去重
                    while(l < r && nums[l] == nums[l + 1])  l ++;
                    while(l < r && nums[r] == nums[r - 1])  r --;
                    l ++; r --;
                }
                else if(nums[i] + nums[l] + nums[r] > 0)
                    r --;
                else
                    l ++;
            }
        }

        return list;
    }
}