算法数据结构

算法学习

发布日期: 2022-08-13

更新日期: 2023-11-15

文章字数: 8.1k

阅读时长: 37 分

一、链表

这里讲解的是用数组模拟链表的实现。

1.1 单链表

应用在使用邻接表来存储的场景中，如树和图的存储。

在图的存储中，head将相应变为h[]数组，h[]数组存储每个链表(节点)的链表头。

// head存储链表头,e[]存储节点的值,ne[]存储节点的next指针,idx表示当前用到了哪个节点
int head, e[N], ne[N], idx;

// 初始化
void init()
{
    head = -1;
    idx = 0;
}

// 在链表头插入一个数x
void insert_head(int x)
{
    e[idx] = x, ne[idx] = head, head = idx++;		//当前idx已经被使用,自增
}

//在k后插入一个数x
void insert(int k,int x)
{
    e[idx] = x, ne[idx] = ne[k], ne[k] = idx++;
}

// 将头结点删除,需要保证头结点存在
void remove_head()
{
    head = ne[head];
}

// 将下标是k的点后面的点删掉
void remove(int k)
{
    ne[k] = ne[ne[k]];
}

注：idx相当于一个分配器，如果需要加入新的结点就用++idx分配出一个下标。

1.2 双链表

// e[]表示节点的值,l[]表示节点的左指针,r[]表示节点的右指针,idx表示当前用到了哪个节点
int e[N], l[N], r[N], idx;

// 初始化
void init()
{
    //0是左端点,1是右端点(边界)
    r[0] = 1, l[1] = 0;
    idx = 2;
}

// 在节点a的右边插入一个数x(若为左边,则调用insert(l[a],x)即可)
void insert(int a, int x)
{
    e[idx] = x;
    l[idx] = a, r[idx] = r[a];
    l[r[a]] = idx, r[a] = idx ++ ;
}

// 删除节点a
void remove(int a)
{
    l[r[a]] = l[a];
    r[l[a]] = r[a];
}

二、栈和队列

栈：后进先出；队列：先进先出

2.1 栈

2.1.1 栈的基本形式

// tt表示栈顶
int stk[N], tt = 0;

// 向栈顶插入一个数
stk[ ++ tt] = x;

// 从栈顶弹出一个数
tt -- ;

// 栈顶的值
stk[tt];

// 判断栈是否为空
if (tt > 0)
{
	//not empty
}

2.1.2 表达式求值

表达式求值依赖表达式树。

如何判断某棵子树被遍历完：当前运算符优先级 $\leq$ 上一个运算符优先级，可用栈来完成。

【具体分析思路】

“假设”我们有一颗二叉树，它的叶子结点是数，其它结点是运算符。

这颗二叉树自根节点至叶子结点运算符的优先级逐级递增，也即根节点的优先级最低。

所以我们只需要将左右子树结果计算出来后，再根据根节点计算最终结点即可。人为去建立一颗这样的树很麻烦，我们可以用栈模拟这样的一个过程。

我们发现，想要计算某个结点的运算符，必要条件是左右子树都已经计算完。

比如：（1+1）（2+2）,显然由于括号的存在，此处‘’的优先级要低于此处的‘+’，我们要计算‘’需要先计算两边的‘+’。

那么就有一个问题：如何判断一个结点的左右子树已经遍历完？

很显然，当我们向上走（换句话说就是当前运算符的优先级低于上一个运算符，因为我们假设存在的这棵树根节点的运算符优先级最低）时，该结点的左右子树已经计算完。也就是这句话：while(!op.empty()&&pr[x]<=pr[op.top()]) eval();在入栈前将栈内优先级更高的运算符计算完再入栈。

另外因为括号无视优先级，需要优先计算括号内的数，那么我们在遇到 ‘)’ 时可以直接将栈内的数从后向前计算出来(在入栈时已经保证了优先级自后向前升高)，直到遇到 ‘(’ 停止。

这样，这棵树就完美的用栈模拟出来了。

例1：二十四点

#include <iostream>
#include <cstring>
#include <algorithm>
#include <stack>
#include <unordered_map>

using namespace std;

stack<int> num;
stack<char> op;

void eval()
{
    int b = num.top(); num.pop();
    int a = num.top(); num.pop();
    char c = op.top(); op.pop();
    int x;
    if (c == '+') x = a + b;
    else if (c == '-') x = a - b;
    else if (c == 'x') x = a * b;
    else
    {
        if (a * b >= 0) x = a / b;
        else  // 向下取整。C++中a/b是向零取整
        {
            if (a % b == 0) x = a / b;
            else x = a / b - 1;
        }
    }
    num.push(x);
}

int main()
{
    unordered_map<char, int> pr;
    pr['+'] = pr['-'] = 1;
    pr['x'] = pr['/'] = 2;
    int n;
    cin >> n;
    while (n -- )
    {
        string str;
        cin >> str;
        num = stack<int>();
        op = stack<char>();
        for (auto c: str)
            if (c >= '0' && c <= '9') num.push(c - '0');
            else
            {
                while (op.size() && pr[op.top()] >= pr[c]) eval();
                op.push(c);
            }
        while (op.size()) eval();
        if (num.top() == 24) puts("Yes");
        else puts("No");
    }
    return 0;
}

python形式：

n = int(input())
while n:
    n -= 1
    res = eval(input().replace('x', '*').replace('/', '//'))
    if res == 24: print("Yes")
    else: print("No")

例2：表达式求值

#include <iostream>
#include <cstring>
#include <algorithm>
#include <stack>
#include <unordered_map>

using namespace std;

stack<int> num;
stack<char> op;

void eval()
{
    auto b = num.top(); num.pop();
    auto a = num.top(); num.pop();
    auto c = op.top(); op.pop();
    int x;
    if (c == '+') x = a + b;
    else if (c == '-') x = a - b;
    else if (c == '*') x = a * b;
    else x = a / b;
    num.push(x);
}

int main()
{
    unordered_map<char, int> pr{{'+', 1}, {'-', 1}, {'*', 2}, {'/', 2}};
    string str;
    cin >> str;
    for (int i = 0; i < str.size(); i ++ )
    {
        auto c = str[i];
        if (isdigit(c))
        {
            int x = 0, j = i;
            while (j < str.size() && isdigit(str[j]))
                x = x * 10 + str[j ++ ] - '0';
            i = j - 1;
            num.push(x);
        }
        else if (c == '(') op.push(c);
        else if (c == ')')
        {
            while (op.top() != '(') eval();
            op.pop();
        }
        else
        {
            while (op.size() && op.top() != '(' && pr[op.top()] >= pr[c]) eval();
            op.push(c);
        }
    }
    while (op.size()) eval();
    cout << num.top() << endl;
    return 0;
}

2.2 队列

2.2.1 普通队列

// hh 表示队头，tt表示队尾
int q[N], hh = 0, tt = -1;

// 向队尾插入一个数
q[ ++ tt] = x;

// 从队头弹出一个数
hh ++ ;

// 队头的值
q[hh];

// 判断队列是否为空
if (hh <= tt)
{
	//not empty
}

2.2.2 循环队列

// hh 表示队头，tt表示队尾的后一个位置
int q[N], hh = 0, tt = 0;

// 向队尾插入一个数
q[tt ++ ] = x;
if (tt == N) tt = 0;

// 从队头弹出一个数
hh ++ ;
if (hh == N) hh = 0;

// 队头的值
q[hh];

// 判断队列是否为空
if (hh != tt)
{
	// 代码块
}

2.3 单调栈

常见模型：找出每个数左边离它最近的比它大/小的数

int tt = 0;
for (int i = 1; i <= n; i ++ )
{
    int x;
    while (tt && check(stk[tt], i)) tt -- ;
    stk[ ++ tt] = x;		// 将x置入栈顶
}

例：单调栈

给定一个长度为 $N$ 的整数数列，输出每个数左边第一个比它小的数，如果不存在则输出 $−1$。

#include <iostream>
using namespace std;

const int N = 100010;
int stk[N], tt;

int main()
{
    int n;
    cin >> n;
    while (n--)
    {
        int x;
        scanf("%d", &x);
        while (tt && stk[tt] >= x)	tt--;	 // 若当前栈顶比x大时,其不会再被用到,直接删去
        if (!tt) printf("-1 ");				// 若栈为空,则输出-1
        	else printf("%d ", stk[tt]);
        stk[ ++ tt] = x;					//将x置入栈顶
    }
    return 0;
}

分析：每个元素只会有一次进栈和出栈操作，算法时间复杂度为O(n)。

2.4 单调队列

常见模型：找出滑动窗口中的最大值/最小值

int hh = 0, tt = -1;
for (int i = 0; i < n; i ++ )
{
    while (hh <= tt && check_out(q[hh])) hh ++ ;  // 判断队头是否滑出窗口
    while (hh <= tt && check(q[tt], i)) tt -- ;
    q[ ++ tt] = i;		// 单调队列记录数组元素的索引值
}

朴素算法—-栈/队列哪些元素是无用的，删去后是否具有单调性—->优化

我们需要维护两个单调队列，单调队列的最大/小值就是队头。

例1：滑动窗口

#include <iostream>
using namespace std;

const int N = 1000010;

int a[N], q[N];		// q数组存放的是元素的下标

int main()
{
    int n, k;
    scanf("%d%d", &n, &k);
    for (int i = 0; i < n; i ++ ) scanf("%d", &a[i]);

    int hh = 0, tt = -1;
    for (int i = 0; i < n; i ++ )
    {
        // 判断队头是否已经滑出了窗口
        if (hh <= tt && i - k + 1 > q[hh])   hh ++ ;

        // 如果当前队尾元素大于新插入的数,队尾将无用,删去
        while (hh <= tt && a[q[tt]] >= a[i]) tt -- ;
        q[ ++ tt] = i;

        if (i >= k - 1) printf("%d ", a[q[hh]]);
    }

    puts("");

    hh = 0, tt = -1;
    for (int i = 0; i < n; i ++ )
    {
        if (hh <= tt && i - k + 1 > q[hh]) hh ++ ;

        while (hh <= tt && a[q[tt]] <= a[i]) tt -- ;
        q[ ++ tt] = i;

        if (i >= k - 1) printf("%d ", a[q[hh]]);
    }

    puts("");

    return 0;
}

例2：烽火传递

烽火台是重要的军事防御设施，一般建在交通要道或险要处。一旦有军情发生，则白天用浓烟，晚上有火光传递军情。在某两个城市之间有 $n$ 座烽火台，每个烽火台发出信号都有一定的代价。

为了使情报准确传递，在连续 $m$ 个烽火台中至少要有一个发出信号。

现在输入 $n,m$ 和每个烽火台的代价，请计算在两城市之间准确传递情报所需花费的总代价最少为多少。

求一维数组选择方案，不妨用集合的思想将问题拆分成一个个子问题来求解，最后合并

集合 $f_i$：第 $1\sim n$ 中以 $i$ 为右端点的区间，选择第 $i$ 个元素的方案，使得方案选的元素总贡献最小

则 $f_i=w_i+min\{f_j\}(1≤i−j≤m)$

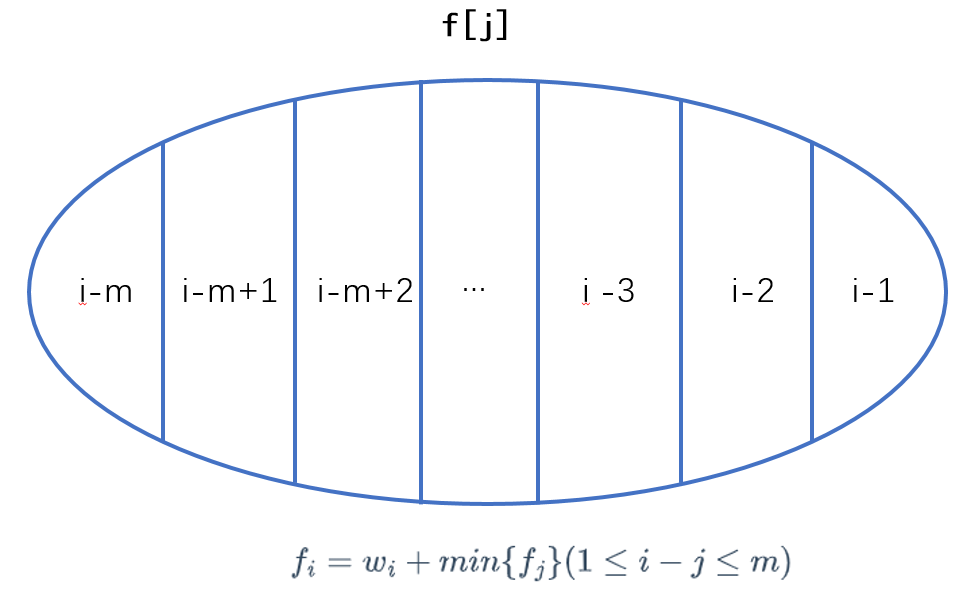
有限范围求最小值函数，直接套单调队列模板即可。

#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 2e5 + 10, INF = 1e9;

int n, m;
int w[N], q[N];
int f[N];

int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i ++ ) scanf("%d", &w[i]);

    int hh = 0, tt = 0;
    for (int i = 1; i <= n; i ++ )
    {
        if (q[hh] < i - m) hh ++ ;
        f[i] = f[q[hh]] + w[i];
        while (hh <= tt && f[q[tt]] >= f[i]) tt -- ;
        q[ ++ tt] = i;
    }

    int res = INF;
    for (int i = n - m + 1; i <= n; i ++ ) res = min(res, f[i]);

    printf("%d\n", res);

    return 0;
}

三、KMP算法

例：KMP字符串

#include <iostream>
using namespace std;

const int N = 100010, M = 1000010;

// s[] 是长文本, p[] 是模式串, n 是 s 的长度, m 是 p 的长度
int n, m;
int ne[N];
char s[M], p[N];

int main()
{
    cin >> n >> p + 1 >> m >> s + 1;

    for (int i = 2, j = 0; i <= n; i ++ )
    {
        while (j && p[i] != p[j + 1]) j = ne[j];
        if (p[i] == p[j + 1]) j ++ ;
        ne[i] = j;
    }

    for (int i = 1, j = 0; i <= m; i ++ )
    {
        while (j && s[i] != p[j + 1]) j = ne[j];
        if (s[i] == p[j + 1]) j ++ ;
        if (j == n)
        {
            printf("%d ", i - n);
            j = ne[j];
        }
    }

    return 0;
}

四、Trie树

用于高效地存储和查找字符串集合的数据结构。

例1：Trie字符串统计

Trie 树是一种用于高效地存储和查找字符串集合的数据结构，它的插入和查询时间复杂度都为 $O(k)$ ，其中 $k$ 为 $key$ 的长度，与树中保存了多少个元素无关。

Trie 树存储字符串的示意图如下所示：

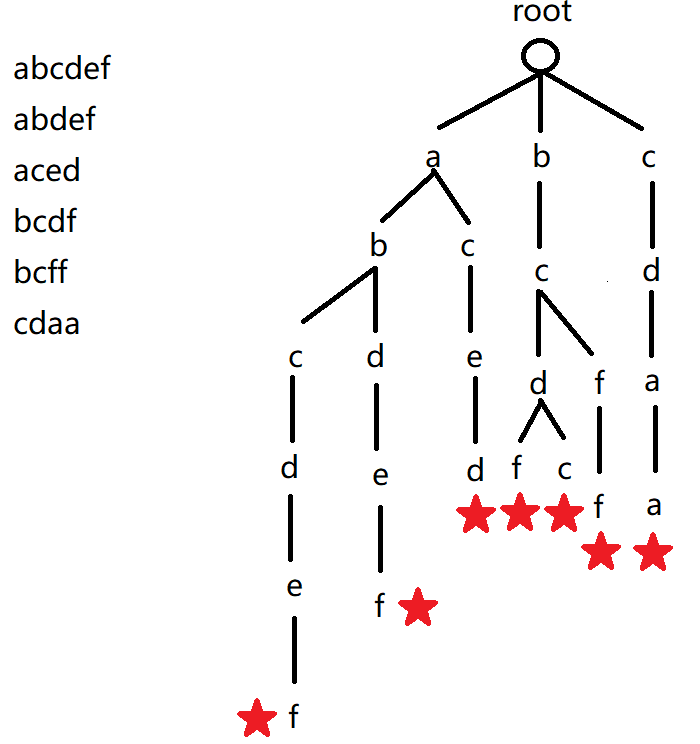
我们运用数据结构表示，有：

0 号点既是根节点，又是空节点，idx 确定每个节点的唯一编号
son[][]存储树中每个节点的子节点，其中该数组的第二维 0-25 对应 a-z
cnt[] 存储以每个节点结尾的单词数量

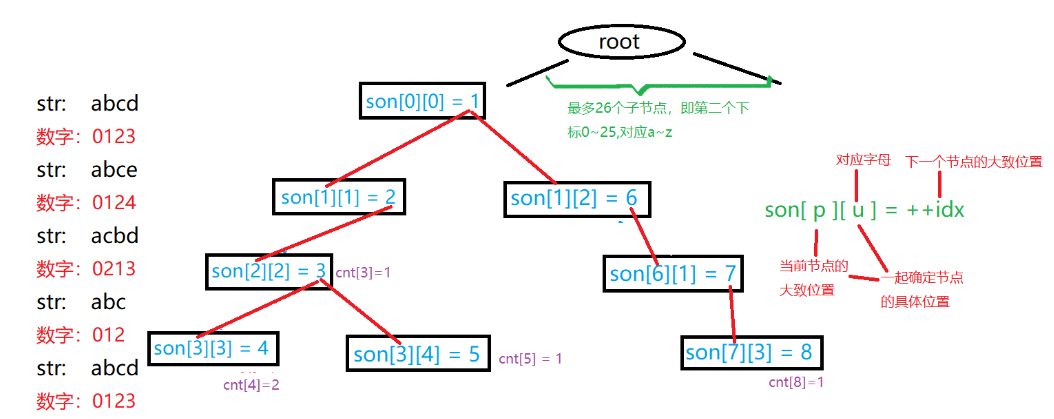
Trie树

int son[N][26], cnt[N], idx;

// 插入一个字符串
void insert(char *str)
{
    int p = 0;		// 根节点
    for (int i = 0; str[i]; i ++ )
    {
        int u = str[i] - 'a';
        if (!son[p][u]) son[p][u] = ++ idx;		// 创建儿子(建一条路)
        p = son[p][u];
    }
    cnt[p] ++ ;
}

// 查询字符串出现的次数
int query(char *str)
{
    int p = 0;
    for (int i = 0; str[i]; i ++ )
    {
        int u = str[i] - 'a';
        if (!son[p][u]) return 0;
        p = son[p][u];		// p 为节点下标
    }
    return cnt[p];
}

相关文章：

如何理解单(双)链表，Trie树和堆中的idx

例2：最大异或和

给定一个非负整数数列 $a$，初始长度为 $N$。

请在所有长度不超过 $M$ 的连续子数组中，找出子数组异或和的最大值。子数组的异或和即为子数组中所有元素按位异或得到的结果。

注意：子数组可以为空。

由异或的性质（两次异或为原值）可知，我们可以转换为前缀和进行优化，可转换为求 $R$ 固定，$S_R\wedge S_{L-1}(R-M\leq L-1 \leq R-1)$ 的最大值，以下同最大异或对。

需要对集合进行以下三个操作，可以用 $Trie$ 树构建：

插入一个数：走一遍，每个路径的结点 $+1$
删除一个数：走一遍，每个路径的结点 $-1$
找到与 $x(即S_R)$ 异或值最大的数

每个比较操作都可以看成在集合中每一位寻找的唯一路径。通过 $Trie$ 树数据结构支持以下操作：

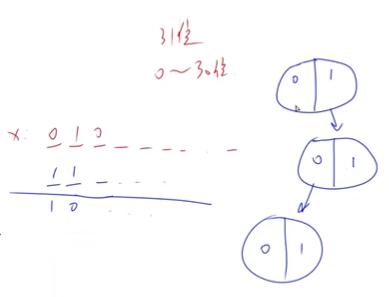
如有以下四个数 $0101,1010,1100,1001$，通过 $Trie$ 树构建以下结构，且在每个节点中记录以该节点为根的子树数。

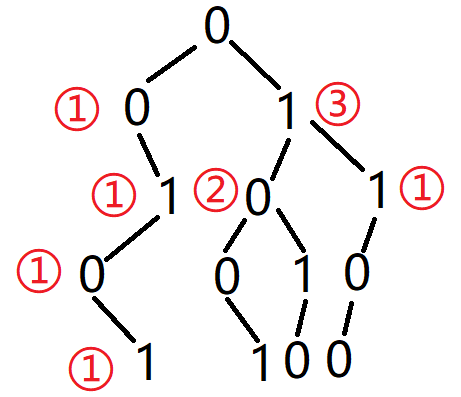
#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 3100010;

int n, m;
int tr[N][2], cnt[N], idx;
int s[N];

void insert(int x, int v)
{
    int p = 0;
    for (int i = 30; i >= 0; i -- )
    {
        int u = x >> i & 1;		// 取出该位
        if (!tr[p][u]) tr[p][u] = ++ idx;
        p = tr[p][u];
        cnt[p] += v;
    }
}

int query(int x)  	// 查询Trie中与x异或和的最大值
{
    int res = 0, p = 0;
    for (int i = 30; i >= 0; i -- )
    {
        int u = x >> i & 1;
        if (cnt[tr[p][!u]]) p = tr[p][!u], res = res * 2 + 1;	// 该位异或和为1
        else p = tr[p][u], res *= 2;	// 该位异或和为0
    }
    return res;
}

int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i ++ )
    {
        int x;
        scanf("%d", &x);
        s[i] = s[i - 1] ^ x;		// 构造前缀和数组
    }

    int res = 0;  		// 空数组
    insert(s[0], 1);	// 没有一个数, 异或和为0, 需加入此值
    for (int i = 1; i <= n; i ++ )
    {
        if (i - m - 1 >= 0) insert(s[i - m - 1], -1);	// 删去该值
        res = max(res, query(s[i]));
        insert(s[i], 1);
    }

    printf("%d\n", res);
    return 0;
}

五、并查集

操作：

将两个集合合并
询问两个元素是否在一个集合之中

并查集在近乎 $O(1)$ 时间内快速支持两个操作。判断图中点的连通性可以用并查集。

基本原理：每个集合用一棵树来表示，树根的编号就是整个集合的编号。每个节点存储它的父节点，p[x]表示x的父节点。

判断树根的方法：if(p[x] == x)
求x的集合编号的方法：while(p[x] != x) x = p[x];
合并两个集合的方法：p[x]是x的集合编号，p[y]是y的集合编号，p[x] = y / p[find(x)] = find(y)(find函数可以返回节点的祖宗节点)

优化(路径压缩)：找到某节点后，将路径中所有节点的前驱都指向根节点

5.1 朴素并查集

find()函数

int p[N]; 					//存储每个点的祖宗节点

// 返回x的祖宗节点 + 路径压缩
int find(int x)
{
	if (p[x] != x) p[x] = find(p[x]);
	return p[x];
}

// 初始化，假定节点编号是 1 ~ n
for (int i = 1; i <= n; i++) p[i] = i;

// 合并 a 和 b 所在的两个集合
p[find(a)] = find(b);

例：合并集合

#include <iostream>
using namespace std;

const int N = 100010;

int p[N];

int find(int x)
{
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

int main()
{
    int n, m;
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i ++ ) p[i] = i;

    while (m--)
    {
        char op[2];
        int a, b;
        scanf("%s%d%d", op, &a, &b);	// 当需要读取一个字母时,使用字符串进行读取
        if (*op == 'M') p[find(a)] = find(b);
        else
        {
            if (find(a) == find(b)) puts("Yes");
            else puts("No");
        }
    }

    return 0;
}

5.2 维护size的并查集

int p[N], size[N];
// p[]存储每个点的祖宗节点, size[]只有祖宗节点的有意义，表示祖宗节点所在集合中的点的数量

// 返回x的祖宗节点
int find(int x)
{
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

// 初始化，假定节点编号是1~n
for (int i = 1; i <= n; i ++ )
{
    p[i] = i;
    size[i] = 1;
}

// 合并a和b所在的两个集合：
size[find(b)] += size[find(a)];
p[find(a)] = find(b);

例：连通块中点的数量

#include <iostream>
using namespace std;

const int N = 100010;

int n, m;
int p[N], cnt[N];

int find(int x)
{
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

int main()
{
    cin >> n >> m;

    for (int i = 1; i <= n; i ++ )
    {
        p[i] = i;
        cnt[i] = 1;
    }

    while (m--)
    {
        string op;
        int a, b;
        cin >> op;

        if (op == "C")
        {
            cin >> a >> b;
            a = find(a), b = find(b);
            if (a != b)
            {
                p[a] = b;
                cnt[b] += cnt[a];
            }
        }
        else if (op == "Q1")
        {
            cin >> a >> b;
            if (find(a) == find(b)) puts("Yes");
            else puts("No");
        }
        else
        {
            cin >> a;
            cout << cnt[find(a)] << endl;
        }
    }

    return 0;
}

六、堆

这里讲述的是手写堆。堆是一个完全二叉树。以小根堆为例，堆使用数组存储，根节点在第一号单元，x的左儿子是2x，右儿子是2x + 1；down(x)往下调整，up(x)往上调整。

堆需要完成以下操作：（下标从1开始）

插入一个数：heap[++size] = x; up(size);
求集合中的最小值：heap[1]
删除最小值：heap[1] = heap[size]; size--; down(1);(将序列最后一个元素取代堆顶，然后进行down操作)
删除任意一个元素：heap[k] = heap[size]; size--; down(k); up(k);
修改任意一个元素：heap[k] = x; down(k); up(k);

6.1 堆排序

例1：堆排序

熟练掌握down()、up()函数

#include<iostream>
#include<algorithm>
using namespace std;

const int N = 100010;

int n, m;
int h[N], cnt;			// cnt为当前堆中的元素个数

void down(int u)
{
    int t = u;			// t为点、左孩子、右孩子三个点中最小的一个点
    if (u * 2 <= cnt && h[u * 2] < h[t]) t = u * 2;
    if (u * 2 + 1 <= cnt && h[u * 2 + 1] < h[t]) t = u * 2 + 1;
    if (u != t)			// 根节点不是最小的
    {
        // 与最小的点交换
        swap(h[u], h[t]);
        down(t);		// 递归处理
    }
}

void up(int u)
{
    while (u / 2 && h[u] < h[u / 2])
    {
        swap(h[u / 2], h[u]);
        u >>= 1;		// u /= 2换上去
    }
}

int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++) scanf("%d", &h[i]);
    cnt = n;

    for (int i = n / 2; i; i--) down(i);	// O(n)的时间复杂度建堆

    while (m--)
    {
        printf("%d ", h[1]);
        h[1] = h[cnt--];
        down(1);
    }

    puts("");

    return 0;
}

6.2 带映射关系的堆排序

例2：模拟堆

#include <iostream>
#include <algorithm>
#include <string.h>

using namespace std;

const int N = 100010;

//ph[j]存储第j个插入的数的下标,hp[k]存储堆内下标为k的点的插入顺序
//ph[j] = k, hp[k] = j	p 下标(pointer), h 堆(heap)
int h[N], ph[N], hp[N], cnt;

void heap_swap(int a, int b)
{
    swap(ph[hp[a]],ph[hp[b]]);
    swap(hp[a], hp[b]);
    swap(h[a], h[b]);
}

void down(int u)
{
    int t = u;
    if (u * 2 <= cnt && h[u * 2] < h[t]) t = u * 2;
    if (u * 2 + 1 <= cnt && h[u * 2 + 1] < h[t]) t = u * 2 + 1;
    if (u != t)
    {
        heap_swap(u, t);
        down(t);
    }
}

void up(int u)
{
    while (u / 2 && h[u] < h[u / 2])
    {
        heap_swap(u, u / 2);
        u >>= 1;
    }
}

int main()
{
    int n, m = 0;
    scanf("%d", &n);
    while (n -- )
    {
        char op[5];
        int k, x;
        scanf("%s", op);
        if (!strcmp(op, "I"))
        {
            scanf("%d", &x);
            cnt ++ ;	//堆的元素加1
            m ++ ;		//第m个插入的数
            ph[m] = cnt, hp[cnt] = m;
            h[cnt] = x;
            up(cnt);
        }
        else if (!strcmp(op, "PM")) printf("%d\n", h[1]);
        else if (!strcmp(op, "DM"))
        {
            heap_swap(1, cnt);
            cnt -- ;
            down(1);
        }
        else if (!strcmp(op, "D"))	//删除第k个插入的位置
        {
            scanf("%d", &k);
            k = ph[k];
            heap_swap(k, cnt);
            cnt -- ;
            up(k);
            down(k);
        }
        else
        {	
            //将第k个插入的数修改
            scanf("%d%d", &k, &x);
            k = ph[k];
            h[k] = x;
            up(k);
            down(k);
        }
    }

    return 0;
}

七、哈希表

存储结构
- 开放寻址法
- 拉链法
字符串哈希方式

时间复杂度为O(1)。

7.1 一般哈希

（1）拉链法

int h[N], e[N], ne[N], idx;

// 向哈希表中插入一个数
void insert(int x)
{
    int k = (x % N + N) % N;
    e[idx] = x;
    ne[idx] = h[k];
    h[k] = idx ++ ;
}

// 在哈希表中查询某个数是否存在
bool find(int x)
{
    int k = (x % N + N) % N;
    for (int i = h[k]; i != -1; i = ne[i])
    {
        if (e[i] == x)
            return true;
    }
    return false;
}

注：

通过memset(h,-1,sizeof h)对h[]数组进行初始化，memset函数按字节来进行初始化，在cpp中每个字节赋-1即每一位都是1，整体结果即为-1。

（2）==开放寻址法==

int h[N];

// 如果x在哈希表中，返回x的下标；如果x不在哈希表中，返回x应该插入的位置
int find(int x)
{
	int t = (x % N + N) % N;
	while (h[t] != null && h[t] != x)	//有人且不是x
	{
		t ++ ;
		if (t == N) t = 0;		//已经到底,循环到第一个坑位
	}
	return t;
}

注：

null可以设为null = 0x3f3f3f3f。

7.2 字符串哈希

字符串哈希的核心思想：
- 将字符串看成P进制数，P的经验值是131或13331，取这两个值的冲突概率低；
- 将其转化为十进制，即$x_{n-1}p^{n-1}+x_{n-2}p^{n-2}+…+x_{0}*p^{0}$，再mod Q，即可将任何一个字符串映射到0 ~ Q - 1之间的数。
小技巧：取模的数用$2^{64}$，这样直接用unsigned long long存储，溢出的结果就是取模的结果。

求前缀的哈希值——->求出所有子串的哈希

$str=[ABCABCD…]$

预处理出所有前缀字母的哈希：

$h[0] = 0$ $h[1] = A的哈希$

$h[2] = AB的哈希$ $h[3] = ABC的哈希$

$h[0] = 0$	$h[1] = A的哈希$
$h[2] = AB的哈希$	$h[3] = ABC的哈希$

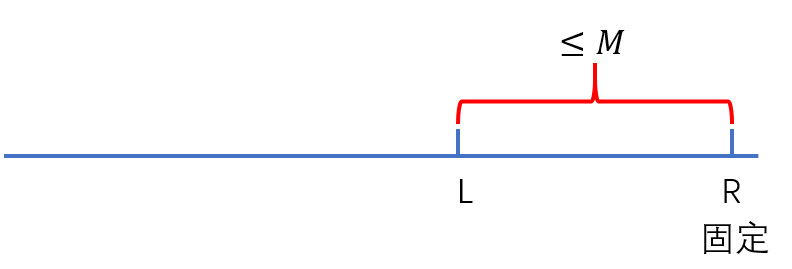
如图，求子串 L 到 R 的哈希值：

求字串的哈希值示意图

$h[R] = p^{R-1}…p^0的哈希$

$h[L-1] = p^{L-2}…p^0的哈希$

将$p^{L-2}…p^0$段字符串与$p^{R-1}…p^0$对齐(即左移，如123左移至123456左端对齐)，则有$h[L-1]*p^{R-L+1}$

子串L到R的哈希值 = $h[R]-h[L-1]*p^{R-L+1}$

hash(DEF) = hash(ABCDEF) - hash(ABC) x P^3
    1       2       3       4       5       6
    A       B       C       D       E       F  
  1xP^5 + 2xP^4 + 3xP^3 + 4xP^2 + 5xP^1 + 6xP^0
  
    A       B       C  
  1xP^2 + 2xP^1 + 3xP^0

                            D       E       F
                          4xP^2 + 5xP^1 + 6xP^0

例：判断两个字符串是否相等

#include <iostream>
#include <algorithm>

using namespace std;

typedef unsigned long long ULL;

const int N = 100010, P = 131;
int n, m;
char str[N];
ULL h[N], p[N];				// h[k]存储字符串前k个字母的哈希值, p[k]存储 P^k mod 2^64

// 计算子串 str[l ~ r] 的哈希值
ULL get(int l, int r)
{
    return h[r] - h[l - 1] * p[r - l + 1];
}

int main()
{
    scanf("%d%d", &n, &m);
    scanf("%s", str + 1);

    // 初始化
    p[0] = 1;
    for (int i = 1; i <= n; i ++ )
    {
        h[i] = h[i - 1] * P + str[i];
        p[i] = p[i - 1] * P;
    }

    while (m -- )
    {
        int l1, r1, l2, r2;
        scanf("%d%d%d%d", &l1, &r1, &l2, &r2);

        if (get(l1, r1) == get(l2, r2)) puts("Yes");
        else puts("No");
    }

    return 0;
}

八、树状数组

解决的基本问题：

快速求前缀和
修改某一个数

时间复杂度都是 $O(logn)$ 的。

将 $x$ 按二进制表示，$x=2^{i_k}+2^{i_{k-1}}+…+2^{i_1}$（各个数分别代表一个二进制位，其中 $i_k\geq i_{k-1} \geq … \geq i_1$，$k\leq logx$），化成以下区间：

$(x-2^{i_1},x]$，区间长度为 $2^{i_1}$，$2^{i_1}$ 是 $x$ 的二进制表示的最后一位 $1$

$(x-2^{i_1}-2^{i_{2}},x-2^{i_1}]$，区间长度为 $2^{i_2}$，$2^{i_2}$ 是 $x-2^{i_1}$ 的二进制表示的最后一位 $1$

……

$(0,x-2^{i_1}-2^{i_{2}}-…-2^{i_{k-1}}]$，区间长度为 $2^{i_k}$，$2^{i_k}$ 是 $x-2^{i_1}-2^{i_{2}}-…-2^{i_{k-1}}$ 的二进制表示的最后一位 $1$

则区间 $[L,R]$ 的长度一定是 $R$ 的二进制表示的最后一位 $1$ 所对应的次幂，则可以表示为 $[R-lowbit(R)+1,R]$

可以用 $C[R]$ 为 $[R-lowbit(R)+1,R]$ 的和，即 $C[x]=a[x-lowbit(x)+1,x]$

通过下述示意图：

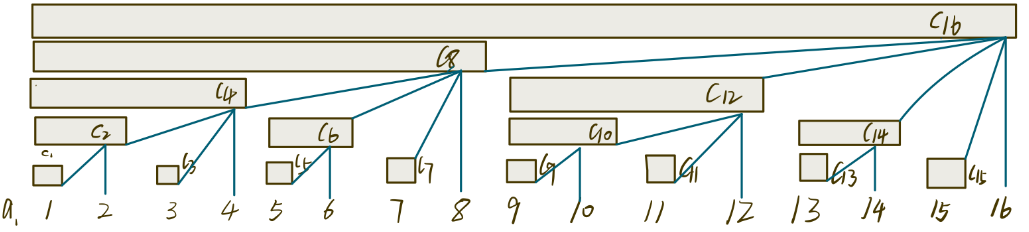
得出不同 $C[i]$ 之间的关系为：

由父节点查找子节点的值（计算 $C[x]$）：$C[x]=a[x]+C[x-1]+C[x-1-lowbit(x-1)]+C[x-1-lowbit(x-1)-lowbit(x-1-lowbit(x-1))]-..$
由子节点查找父节点的值（对应修改操作）：查找所有包含子节点的区间，有 $P=x+lowbit(x)$，且每个子节点直接影响到的点均只有一个（迭代的过程）

lowbit:

int lowbit(int x)
{
    return x & -x;
}

查询：

for(int i = x; i; i -= lowbit(i)) sum += tr[i];

修改：

for(int i = x; i <= n; i += lowbit(i)) tr[i] += c;

例：楼兰图腾

在完成了分配任务之后，西部 $314$ 来到了楼兰古城的西部。

相传很久以前这片土地上(比楼兰古城还早)生活着两个部落，一个部落崇拜尖刀(V)，一个部落崇拜铁锹(∧)，他们分别用 V 和 ∧ 的形状来代表各自部落的图腾。

西部 $314$ 在楼兰古城的下面发现了一幅巨大的壁画，壁画上被标记出了 $n$ 个点，经测量发现这 $n$ 个点的水平位置和竖直位置是两两不同的。

西部 $314$ 认为这幅壁画所包含的信息与这 $n$ 个点的相对位置有关，因此不妨设坐标分别为 $(1,y_1),(2,y_2),…,(n,y_n)$，其中 $y_1∼y_n$ 是 $1$ 到 $n$ 的一个排列。

西部 $314$ 打算研究这幅壁画中包含着多少个图腾。

如果三个点 $(i,y_i),(j,y_j),(k,y_k)$ 满足 $1≤iy_j,y_j<y_k$，则称这三个点构成 V 图腾;

如果三个点 $(i,y_i),(j,y_j),(k,y_k)$ 满足 $1≤iy_k$，则称这三个点构成 ∧ 图腾;

西部 $314$ 想知道，这 $n$ 个点中两个部落图腾的数目。

因此，你需要编写一个程序来求出 V 的个数和 ∧ 的个数。

思路：

分成 $n$ 类，每类可以以每个点为界限，找左边比自己大的*右边比自己大的，累加求的 V 的值。
$y_1∼y_n$ 是 $1$ 到 $n$ 的一个排列，即 $y$ 的取值是在 $[1,n]$ 且每一个 $y$ 不重复。
将 $y$ 的值看成 $tr$ 数组的下标，因此求出来的 $sum[x]$ 值，就是小于 $x$ 数个数。

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

typedef long long LL;

const int N = 200010;

int n;
int a[N];
int tr[N];
int Greater[N], lower[N];

int lowbit(int x)
{
    return x & -x;
}

void add(int x, int c)
{
    for (int i = x; i <= n; i += lowbit(i)) tr[i] += c;
}

int sum(int x)
{
    int res = 0;
    for (int i = x; i; i -= lowbit(i)) res += tr[i];
    return res;
}

int main()
{
    scanf("%d", &n);

    for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);

    // 从左往右遍历, 求 1 到 k - 1 中有多少大/小于 yk
    for (int i = 1; i <= n; i ++ )
    {
        int y = a[i];
        Greater[i] = sum(n) - sum(y);		// 值在 y + 1 到 n 中有多少个数
        lower[i] = sum(y - 1);			   // 值在 1 到 y - 1 中有多少个数
        add(y, 1);						  // 将其加到集合中去
    }

    memset(tr, 0, sizeof tr);
    LL res1 = 0, res2 = 0;
    // 从右往左遍历, 求 k + 1 到 n 中有多少大/小于 yk
    for (int i = n; i; i -- )
    {
        int y = a[i];
        res1 += Greater[i] * (LL)(sum(n) - sum(y));
        res2 += lower[i] * (LL)(sum(y - 1));
        add(y, 1);
    }

    printf("%lld %lld\n", res1, res2);

    return 0;
}

九、C++ STL

9.1 vector

变长数组：倍增的思想

size()  返回元素个数
empty()  返回是否为空
clear()  清空
front() / back()
push_back() / pop_back()
begin() / end()
reverse(v1.begin(),v1.end());

遍历的三种形式：

//1
for (int i = 0; i < 10; i++) cout << a[i] << ' ';
cout << endl;
//2
for (auto i = a.begin(); i != a.end(); i++) cout << *i << ' ';
cout << endl;
//3
for (auto x : a) cout << x << ' ';
cout << endl;

删除指定元素：

for (auto it = mou.begin(); it != mou.end();) 
{
	if (it[0].l <= max && it[0].r >= max)
		it = mou.erase(it);
	else
		++it;
}

支持比较运算，按字典序：

vector<int> a(4,3),b(3,4) //a初始化4个3，则有a<b。

9.2 pair

需引入头文件#include <utility>。

first, 第一个元素
second, 第二个元素

支持比较运算，以first为第一关键字，以second为第二关键字（字典序）。

pair相当于两个变量的结构体+比较函数。

pair<int, string> p;
p = make_pair(10, "yxc");
p = { 20,"abc" };
//存储三种属性
pair<int, pair<int,int>> p;

9.3 string

字符串string a = "yxc";

a += "def";			加到字符串末尾
size() / length()    返回字符串长度
empty()
clear()
substr(起始下标,(子串长度))  返回子串
c_str()  返回字符串所在字符数组的起始地址	// printf("%s\n",a.c_str());
to_string(num).find('7') != -1			// 判断数中是否含有数字7

读取多组测试数据，且遇到空格不间断，使用以下语句：

while (getline(cin, str))

9.4 队列

9.4.1 queue

队列：queue<int> q;

size()
empty()
push()  向队尾插入一个元素
front() 返回队头元素
back()  返回队尾元素
pop()   弹出队头元素
q = queue<int>();		//清空队列

9.4.2 priority_queue

优先队列，默认是大根堆。

priority_queue<int> heap;
    size()
    empty()
    push()  插入一个元素
    top()   返回堆顶元素
    pop()   弹出堆顶元素
定义成小根堆的方式：priority_queue<int, vector<int>, greater<int>> q;

9.4.3 deque

双端队列

size()
empty()
clear()
front() / back()
push_back() / pop_back()
push_front() / pop_front()		//从队首弹出一元素
begin() / end()
[]							  //支持随机访问

deque的常用成员函数

9.5 stack

栈stack

size()
empty()
push()  向栈顶插入一个元素
top()   返回栈顶元素
pop()   弹出栈顶元素

9.6 set和map

9.6.1 set, map, multiset, multimap

基于平衡二叉树（红黑树），动态维护有序序列。

size()
empty()
clear()
begin()/end()
	访问最后一个元素的值: *(--data1.end())
++, -- 返回前驱和后继 时间复杂度为 O(logn)

set/multiset(set不能有重复元素,multiset可以)
    insert()  插入一个数
    find()  查找一个数,不存在则返回end迭代器
    count()  返回某一个数的个数
    erase()
       (1) 输入是一个数x，删除所有x   O(k + logn)
       (2) 输入一个迭代器，删除这个迭代器
    //离散数学中的最小上界
    lower_bound()/upper_bound()
       lower_bound(x)  返回大于等于x的最小的数的迭代器
       upper_bound(x)  返回大于x的最小的数的迭代器
    遍历:
	for(auto i = order.begin(); i != order.end(); i++){
            cout<< *i << endl;
     }
map/multimap
    insert()  插入的数是一个pair
    erase()  输入的参数是pair或者迭代器
    find()
    	map<int, string>::iterator iter = node.find(123456);
    	if(iter != node.end()){}
		or if(node.find(num - 1) != node.end())	(***)
    []  注意multimap不支持此操作。 时间复杂度是 O(logn)
    lower_bound()/upper_bound()
    遍历:
    for(auto it : map1){
        cout << it.first <<" "<< it.second <<endl;
    }
Example:
    map<string,int> a;
    a["yxc"] = 1;
    cout << a["yxc"] << endl;	//可和数组一样来取数据,但时间复杂度比数组高

9.6.2 unordered_set, unordered_map, unordered_multiset, unordered_multimap

基于哈希表。

和上面类似，增删改查的时间复杂度是 O(1)
不支持基于排序的操作：lower_bound()/upper_bound()，迭代器的++，—
支持判断相等==

9.7 bitset

压位，每个字节中存八位

bitset<10000> s;	//<>中写明个数
//支持位运算操作
~, &, | , ^
>> , <<
==, !=
//支持随机访问
[]

count()    返回有多少个1

any()      判断是否至少有一个1
none()     判断是否全为0

set()  	   把所有位置成1
set(k, v)  将第k位变成v
reset()    把所有位变成0
flip()     等价于~
flip(k)    把第k位取反

存储数字的二进制：

bitset<N> name(num);，意即定义长度为N的二进制数组，命名为name，将数字num的二进制存到其中
bitset<8> b2(12); 	 // 二进制长度8，将12转化为二进制存到其中
存储01字符串对应的二进制：

bitset<N> name(string); ，意即定义长度为N的二进制数组，命名为name，将01串string存到其中，长度不够前补 0，长度过长截断
string s = "10010";
bitset<8> b3(s);
cout << b3 << endl;

9.8 lambda表达式

lambda 表达式是一种能够创建匿名函数的方式，可以将其作为参数传递给其他函数，例如将 lambda 表达式作为 stable_sort 函数的第三个参数：

// stable_sort函数可以进行稳定排序
stable_sort(cs.begin(), cs.end(), [](char a, char b) {
      return tolower(a) < tolower(b);
});

Tips：关于Java有关

重写 `equals` 方法

@Override
public boolean equals(Object obj) {
    //判断内存地址
    if (obj == this) {
        return true;
    }
    if (obj == null) {
        return false;
    }
    //判断是否是同一类型的对象
    if (obj instanceof Person) {
    //强制转换成Person类型
        Person per = (Person) obj;
        //判断他们的属性值
        if (this.name.equals(per.name) && this.age == (per.age)) {
            return true;
        }
    }
    return false;
}

遍历 `Map`

for (Map.Entry<Integer, Integer> entry : countMap.entrySet()) {
    if (entry.getValue() >= threshold) {
        System.out.println("数字 " + entry.getKey() + " 出现了 " + entry.getValue() + " 次，占比达到了10%以上");
    }
}

排序语法

// 创建一个Comparator对象，通过指定的比较逻辑来对数组中的元素进行排序。
// 在这个Lambda表达式中，a -> a[0]表示将数组中的每个元素a作为输入，提取其中的索引为0的值作为比较依据。
Arrays.sort(intervals, Comparator.comparingInt(a -> a[0]));

ShiQuLiZhi

https://www.qqzzss.top/2022/08/13/algorithmlearning/suan-fa-02-shu-ju-jie-gou/

本博客所有文章除特别声明外，均采用 CC BY 4.0 许可协议。转载请注明来源 ShiQuLiZhi !

算法数据结构

算法3:搜索与图论

2022-08-13 算法学习

算法数据结构

算法1:基础算法

2022-08-13 算法学习

算法数据结构

算法2:数据结构

一、链表

1.1 单链表

1.2 双链表

二、栈和队列

2.1 栈

2.1.1 栈的基本形式

2.1.2 表达式求值

2.2 队列

2.2.1 普通队列

2.2.2 循环队列

2.3 单调栈

2.4 单调队列

三、KMP算法

四、Trie树

五、并查集

5.1 朴素并查集

5.2 维护size的并查集

六、堆

6.1 堆排序

6.2 带映射关系的堆排序

七、哈希表

7.1 一般哈希

7.2 字符串哈希

八、树状数组

九、C++ STL

9.1 vector

9.2 pair

9.3 string

9.4 队列

9.4.1 queue

9.4.2 priority_queue

9.4.3 deque

9.5 stack

9.6 set和map

9.6.1 set, map, multiset, multimap

9.6.2 unordered_set, unordered_map, unordered_multiset, unordered_multimap

9.7 bitset

9.8 lambda表达式

Tips：关于Java有关

重写 equals 方法

遍历 Map

排序语法

重写 `equals` 方法

遍历 `Map`