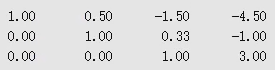一、质数与约数

在大于 $1$ 的整数中，如果只包含 $1$ 和本身这两个约数，就被称为质数/素数。

1.1 质数的判定

试除法判定质数：

有性质：若 d|n，则 n/d|n。

bool is_prime(int x)
{
    if (x < 2) return false;
    for (int i = 2; i <= x / i; i ++ )
        if (x % i == 0)
            return false;
    return true;
}

1.2 分解质因数

试除法分解质因数：

$n = p_{1}^{\alpha_{1}}…p_{k}^{\alpha_{k}}$

void divide(int x)
{
    for (int i = 2; i <= x / i; i ++ )
        if (x % i == 0)		//若此条件成立,i一定是质数
        {
            int s = 0;		//s为次数
            while (x % i == 0) x /= i, s ++ ;
            cout << i << ' ' << s << endl;
        }
    if (x > 1) cout << x << ' ' << 1 << endl;	//单独处理,唯一一个大于sqrt(n)的质因子
    cout << endl;
}

注：

由于 $n$ 不包含任何从 $2$ 到 $i-1$ 之间的质因子（已经被除干净了），若x % i = 0成立，i不包含其中的所有质因子，故i一定是质数；

n中最多只包含一个大于sqrt(n)的质因子；

当n = 2^k时，时间复杂度为O(log n)，而最坏时间复杂度为O(sqrt(n))，平均情况是介于两者之间。

1.3 筛素数

例：筛素数

给定一个正整数n，请你求出1∼n中质数的个数。

1.3.1 朴素筛法筛素数

int primes[N], cnt;     						// primes[]存储所有素数
bool st[N];        								// st[x]存储x是否被筛掉

void get_primes(int n)
{
    for (int i = 2; i <= n; i ++ )
    {
        if (st[i]) continue;					// 被筛过
        primes[cnt ++ ] = i;
        for (int j = i + i; j <= n; j += i)		 // 把i的倍数全部筛去
            st[j] = true;
    }
}

1.3.2 线性筛法筛素数

n 只会被最小质因子筛掉：

i % primes[j] == 0：primes[j]一定是i的最小质因子，primes[j]一定是primes[j] * i的最小质因子
i % primes[j] != 0：primes[j]一定小于i的最小质因子，primes[j]也一定是primes[j] * i的最小质因子

对于一个合数 x，假设 primes[j] 是 x 的最小质因子，当 i 枚举到 x / primes[j] 时，将会筛掉，每个合数只会被筛掉一次。

int primes[N], cnt;     						// primes[]存储所有素数
bool st[N];         							// st[x]存储x是否被筛掉

void get_primes(int n)
{
    for (int i = 2; i <= n; i ++ )
    {
        if (!st[i]) primes[cnt ++ ] = i;
        for (int j = 0; primes[j] <= n / i; j ++ )
        {
            st[primes[j] * i] = true;
            if (i % primes[j] == 0) break;		// primes[j]一定是i的最小质因子
        }
    }
}

1.4 约数

1.4.1 试除法求一个数的所有约数

vector<int> get_divisors(int x)
{
    vector<int> res;
    for (int i = 1; i <= x / i; i ++ )
    {
        if (x % i == 0)
        {
            res.push_back(i);
            if (i != x / i) res.push_back(x / i);
        }
    }
    sort(res.begin(), res.end());
    return res;
}

1.4.2 约数个数

基于算术基本定理：

若$N = p_{1}^{\alpha_{1}} p_{2}^{\alpha_{2}} … p_{k}^{\alpha_{k}}$，$N$ 的任意一个约数 $d$ 也可以写为 $d = p_{1}^{\beta_{1}} p_{2}^{\beta_{2}} … p_{k}^{\beta_{k}}$，其中 $0\leq \beta_{i} \leq \alpha _{i}$。

$\beta_{i}$ 有 $0-\alpha_{1}$ 共 $(\alpha_{1} + 1)$ 种选法，则 $N$ 共有$(\alpha_{1} + 1)(\alpha_{2} + 1)…(\alpha_{k} + 1)$个约数。

例：求约数个数

#include <iostream>
#include <algorithm>
#include <unordered_map>
#include <vector>

using namespace std;

typedef long long LL;

const int N = 110, mod = 1e9 + 7;

int main()
{
    int n;
    cin >> n;

    unordered_map<int, int> primes;

    while (n -- )
    {
        int x;
        cin >> x;

        for (int i = 2; i <= x / i; i ++ )
            while (x % i == 0)
            {
                x /= i;
                primes[i] ++ ;
            }

        if (x > 1) primes[x] ++ ;
    }

    LL res = 1;
    for (auto p : primes) res = res * (p.second + 1) % mod;

    cout << res << endl;

    return 0;
}

1.4.3 约数之和

$(p_{1}^{0}+p_{1}^{1}+…+p_{1}^{\alpha_{1}})…(p_{k}^{0}+p_{k}^{1}+…+p_{k}^{\alpha_{k}})$

例：约数之和

#include <iostream>
#include <algorithm>
#include <unordered_map>
#include <vector>

using namespace std;

typedef long long LL;

const int N = 110, mod = 1e9 + 7;

int main()
{
    int n;
    cin >> n;

    unordered_map<int, int> primes;

    while (n -- )
    {
        int x;
        cin >> x;

        for (int i = 2; i <= x / i; i ++ )
            while (x % i == 0)
            {
                x /= i;
                primes[i] ++ ;
            }

        if (x > 1) primes[x] ++ ;
    }

    LL res = 1;
    for (auto p : primes)
    {
        LL a = p.first, b = p.second;
        LL t = 1;
        while (b -- ) t = (t * a + 1) % mod;		//注1
        res = res * t % mod;
    }

    cout << res << endl;

    return 0;
}

注：对代码1while (b -- ) t = (t * a + 1) % mod;的注释：

对t = 1，每次执行t = p * t + 1，执行结果分别为p + 1,p^2 + p + 1,…执行$\alpha$次得到$p^{0}+p^{1}+…+p^{\alpha}$。

1.4.4 最大公约数:欧几里得算法

也称辗转相除法。

若d|a，d|b，则d|(ax + by)。有结论：(a,b) = (b,a mod b)。

证明：

$a\mod b = a - \lfloor a/b \rfloor * b = a - c *b$(其中c为一整数)。则只需证明(a,b) = (b,a - c * b)即可。

对于左边任意一个公约数，由d|a，d|b，故d|a - c * b；

对于右边任意一个公约数，由d|a - c * b，又d|b，则有d|a - c * b + c * b，即d|a。

则左边的最大公约数 = 右边的最大公约数，故有(a,b) = (b,a mod b)。

int gcd(int a, int b)
{
    return b ? gcd(b, a % b) : a;
}

二、数学定理

2.1 欧拉函数

2.1.1 求欧拉函数

$1-N$中与$N$互质的数的个数称为欧拉函数，记为$\phi(N)$。

若$N = p_{1}^{\alpha_{1}}p_{2}^{\alpha_{2}}…p_{k}^{\alpha_{k}}$，则有$\phi(N) = N(1-\frac{1}{p_{1}})(1-\frac{1}{p_{2}})…(1-\frac{1}{p_{k}})$。

如：$N=6=2 * 3$，则$\phi(N) = 6*(1-\frac{1}{2})(1-\frac{1}{3})=2$。

证明：容斥原理

要计算$1-N$中与$N$互质的数的个数：

从$1-N$中去掉$p_{1},p_{2},…,p_{k}$的倍数

加上所有$p_{i}*p_{j}$的倍数

去掉所有$p_{i}*p_{j}*p_{k}$的倍数

……

则有$N-\frac{N}{p_{1}}-\frac{N}{p_{2}}-…-\frac{N}{p_{k}}+\frac{N}{p_{1}p_{2}}+\frac{N}{p_{1}p_{3}}+…-\frac{N}{p_{1}p_{2}p_{3}}-\frac{N}{p_{2}p_{3}p_{4}}+\frac{N}{p_{1}p_{2}p_{3}p_{4}}+…$，展开后即为上式。

int phi(int x)
{
    int res = x;
    for (int i = 2; i <= x / i; i ++ )
        if (x % i == 0)						//分解质因数
        {
            res = res / i * (i - 1);
            while (x % i == 0) x /= i;
        }
    if (x > 1)	res = res / x * (x - 1);

    return res;
}

2.1.2 筛法求欧拉函数

例：筛法求欧拉函数

int primes[N], cnt;     				// primes[]存储所有素数
int euler[N];          					// 存储每个数的欧拉函数
bool st[N];         					// st[x]存储x是否被筛掉

void get_eulers(int n)
{
    euler[1] = 1;
    for (int i = 2; i <= n; i ++ )
    {
        if (!st[i])
        {
            primes[cnt ++ ] = i;		//i为质数
            euler[i] = i - 1;			//质数的欧拉函数为i - 1
        }
        for (int j = 0; primes[j] <= n / i; j ++ )
        {
            int t = primes[j] * i;
            st[t] = true;
            if (i % primes[j] == 0)
            {
                euler[t] = euler[i] * primes[j];		//注1
                break;
            }
            euler[t] = euler[i] * (primes[j] - 1);		//注2
        }
    }
}

注：

[1]：对euler[t] = euler[i] * primes[j];语句的注释：

对于$\phi(i)$，有$\phi(i) = i (1-\frac{1}{p_{1}})…*(1-\frac{1}{p_{k}})$。而由于$i \mod p_{j} == 0$，故$p_{j}$是$i$的一个质因子，则有：

$\phi(p_{j}*i)= p_{j}i (1-\frac{1}{p_{1}})…(1-\frac{1}{p_{k}}) = p_{j}*\phi(i)$。

[2]：对euler[t] = euler[i] * (primes[j] - 1);语句的注释：

当$i \mod p_{j} \neq 0$时，$\phi(i) = i (1-\frac{1}{p_{1}})…*(1-\frac{1}{p_{k}})$，$\phi(p_{j}i)= p_{j}i (1-\frac{1}{p_{1}})…(1-\frac{1}{p_{k}})(1-\frac{1}{p_{j}}) = \phi(i)p_{j}(1-\frac{1}{p_{j}}) = \phi(i)(p_{j} - 1)$。

2.1.3 欧拉定理

若a与n互质，则$a^{\phi(n)} \equiv 1(\mod n)$。若n是质数，则有$a^{n-1} \equiv 1(\mod n)$(费马小定理)。

证明：

在1-n中有$a_{1},a_{2},…,a_{\phi(n)}$个数与n互质。由于a与n互质，则有$aa_{1},aa_{2},…,aa_{\phi(n)}$个数与n互质。则有$a_{1},a_{2},…,a_{\phi(n)}$与$aa_{1},aa_{2},…,aa_{\phi(n)}$是同一组数，只是顺序不同。故它们的乘积(模n)是相等的，即有：

$a^{\phi(n)}*(a_{1}a_{2}…a_{\phi(n)})\equiv (a_{1}a_{2}…a_{\phi(n)}) \mod n$。

由于$(a_{1}a_{2}…a_{\phi(n)})$与$n$互质，则可以消去，直接写为：

$a^{\phi(n)} \equiv 1 (\mod n)$

ps：我们可将$(a_{1}a_{2}…a_{\phi(n)})$记作$k$，$(a^{\phi(n)} - 1)$记作$a$，全部提到左边，有$a * k \equiv 0(\mod n)$。而$k$与$n$互质，说明$k$不是$n$的因数，而$a * k$能被$n$整除，说明另外一个数(即$a$)可以被$n$整除。例：$5 * 6 = 0 \mod 3$，5和3互质，两边同时除以5，$6 = 0 \mod 3$仍正确。

2.2 快速幂

在时间复杂度为O(logk)的情况下求$a^k \mod p$的结果。

首先预处理logk个数，之后可用这些数运算的结果快速得到答案。计算：

$a^{2^{0}}\mod p = a^{1} \mod p$，

$a^{2^{1}}\mod p = a^{2^{0}*2} = (a^{2^{0}})^{2}\mod p$，

$a^{2^{2}}\mod p = a^{2^{2}*2} = (a^{2^{1}})^{2}\mod p$，

……,

$a^{2^{logk}}\mod p = a^{2^{0}*2} = (a^{2^{logk - 1}})^{2}\mod p$.

即所有数都是前一个数的平方。计算完这些值后(实际代码编写是同步完成的)，将$a^k \mod p$中的k进行位运算。如：$(k){10} = (110110){2}$，则$k = 2^{1}+2^{2}+2^{4}+2^{5}$。然后即可根据以下等式计算结果：

$a^{k} = a^{2^{x_{1}}+2^{x_{2}}+…+2^{x_{t}}}=a^{2^{x_{1}}}a^{2^{x_{2}}}…a^{2^{x_{t}}}(\mod p)$.

typedef long long LL;
// a^k % p
LL qmi(int a, int k, int p)
{
    LL res = 1 % p;
    while (k)
    {
        if (k & 1) res = (LL)res * a % p;	  //k的该位如果是1,将对应位结果相乘
        k >>= 1;							//将k的末位删去
        a = (LL)a * a % p;					 //将a平方
    }
    return res;
}

例：快速幂求逆元

【乘法逆元的定义】

若整数b,m互质，并且对于任意的整数a，如果满足b|a，则存在一个整数x，使得 a/b≡a * x(mod m)，则称x为b的模m乘法逆元，记为$b^{−1}(\mod m)$。

有性质：$b * b^{−1} = 1(\mod m)$.

特别地，对质数b来说，若有$b * x \equiv 1(\mod p)$，而由费马小定理，$b^{p-1} \equiv 1(\mod p)$，则$b * b^{p-2} \equiv 1(\mod p)$，则模p乘法逆元为$b^{p-2}$。

例：快速幂求逆元【题目中的p规定为质数】

#include <iostream>
#include <algorithm>
using namespace std;

typedef long long LL;

LL qmi(int a, int b, int p)
{
    LL res = 1;
    while (b)
    {
        if (b & 1) res = res * a % p;
        a = a * (LL)a % p;
        b >>= 1;
    }
    return res;
}

int main()
{
    int n;
    scanf("%d", &n);
    while (n -- )
    {
        int a, p;
        scanf("%d%d", &a, &p);
        if (a % p == 0) puts("impossible");			//若a是p的倍数,一定无解
        else printf("%lld\n", qmi(a, p - 2, p));
    }

    return 0;
}

2.3 拓展欧几里得算法

裴蜀定理：对于任意一对正整数a,b，一定存在非零整数x,y，使得ax + by = (a,b)。

// 求x, y，使得ax + by = gcd(a, b)
int exgcd(int a, int b, int &x, int &y)
{
    if (!b)
    {
        x = 1; y = 0;
        return a;
    }
    int d = exgcd(b, a % b, y, x);		// by + (a % b)x = (b,a % b) = (a,b)
    y -= (a/b) * x;						// 注1
    return d;
}

注：

[1]对y -= (a/b) * x;语句的注释：

$by + (a \mod b)x = d$->$by + (a-\lfloor \frac{a}{b}\rfloor*b)x = d$->$ax + b(y-\lfloor \frac{a}{b}\rfloor x) = d$

则有y -= (a/b) * x;

[2]当模的数字是质数时，可用费马小定理求逆元，否则只能使用拓展欧几里得算法求解。

例：线性同余方程

给定n组数据$a_{i},b_{i},m_{i}$，对于每组数求出一个$x_{i}$，使其满足$a_{i}*x_{i}≡b_{i}(\mod m_{i})$。

等价于，$\exists y\in Z,st. ax = my +b$->$ax-my = b$。令$y^{‘} = y$，则$ax+my^{‘} = b$。

等价于该式有解，有解条件是(a,m)|b。

#include <iostream>
#include <algorithm>
using namespace std;

typedef long long LL;

int exgcd(int a, int b, int &x, int &y)
{
    if (!b)
    {
        x = 1, y = 0;
        return a;
    }
    int d = exgcd(b, a % b, y, x);
    y -= a / b * x;
    return d;
}


int main()
{
    int n;
    scanf("%d", &n);
    while (n -- )
    {
        int a, b, m;
        scanf("%d%d%d", &a, &b, &m);

        int x, y;
        int d = exgcd(a, m, x, y);
        if (b % d) puts("impossible");
        else printf("%d\n", (LL)b / d * x % m);		//扩大b / d倍
    }

    return 0;
}

2.4 中国剩余定理

给定一些两两互质的数$m_{1},m_{2},…,m_{k}$，求解线性同余方程组：

$\begin{cases} x \equiv a_{1}(\mod m_{1}) \ x \equiv a_{2}(\mod m_{2})\ … \ x \equiv a_{k}(\mod m_{k})\end{cases}$

令$M = m_{1}m_{2}…m_{k}$，$M_{i} = \frac{M}{m_{i}}$，$M_{i}^{-1}$表示$M_{i}$模$m_{i}$的逆，则公式解为：

$x = a_{1}M_{1}M_{1}^{-1}+a_{2}M_{2}M_{2}^{-1}+…+a_{k}M_{k}M_{k}^{-1}(\mod M)$

三、高斯消元

高斯消元可在$O(n^{3})$的时间复杂度内求解下列方程组：

$\begin{cases}
a_{11} x_{1}+a_{12} x_{2}+\cdots+a_{1 n} x_{n}=b_{1} \
a_{21} x_{1}+a_{22} x_{2}+\cdots+a_{2 n} x_{n}=b_{2} \
\cdots \
a_{m 1} x_{1}+a_{m 2} x_{2}+\cdots+a_{m n} x_{n}=b_{m}
\end{cases}$

解的情况有：无解、无穷多组解、唯一解。

进行以下三种初等行列变换，不会改变解：

把某一行乘一个非零的数
交换某2行
把某行的若干倍加到另一行上去

变换后：

完美阶梯形——唯一解
0=非零——无解
0=0(该方程可以被其他方程表示)——无穷多组解

高斯消元的算法步骤：

枚举每一列C

找到当前列绝对值最大的一行
将该行换到最上面
将该行第1个数变成1
将下面所有行的当前列消成0

枚举完后，该矩阵变为上三角形式：

$\begin{pmatrix} 1 & 0 & 0 & 1\ 0 & 1 & 0 & -2\ 0 & 0 & 1 & 3\end{pmatrix}$

即有$x_{1}+0x_{2}+0x_{3} = 1$等式，求出结果。

高斯消元最后一步

例：高斯消元解线性方程组

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>

using namespace std;

const int N = 110;
const double eps = 1e-8;

int n;
double a[N][N];

int gauss()  		// 高斯消元，答案存于a[i][n]中，0 <= i < n
{
    int c, r;
    for (c = 0, r = 0; c < n; c ++ )
    {
        int t = r;
        for (int i = r; i < n; i ++ )  							// 找绝对值最大的行
            if (fabs(a[i][c]) > fabs(a[t][c]))
                t = i;

        if (fabs(a[t][c]) < eps) continue;			 // 说明该数是0,fabs返回浮点数类型的绝对值

        for (int i = c; i <= n; i ++ ) swap(a[t][i], a[r][i]);  // 将绝对值最大的行换到最顶端
        for (int i = n; i >= c; i -- ) a[r][i] /= a[r][c];  	// 将当前行的首位变成1,注意最后更新第一个数
        for (int i = r + 1; i < n; i ++ )  						// 用当前行将下面所有的列消成0
            if (fabs(a[i][c]) > eps)							// 不是0才操作
                for (int j = n; j >= c; j -- )
                    a[i][j] -= a[r][j] * a[i][c];

        r ++ ;
    }

    if (r < n)
    {
        for (int i = r; i < n; i ++ )
            if (fabs(a[i][n]) > eps)
                return 2; 						// 0 = 非零,无解
        return 1; 								// 有无穷多组解
    }

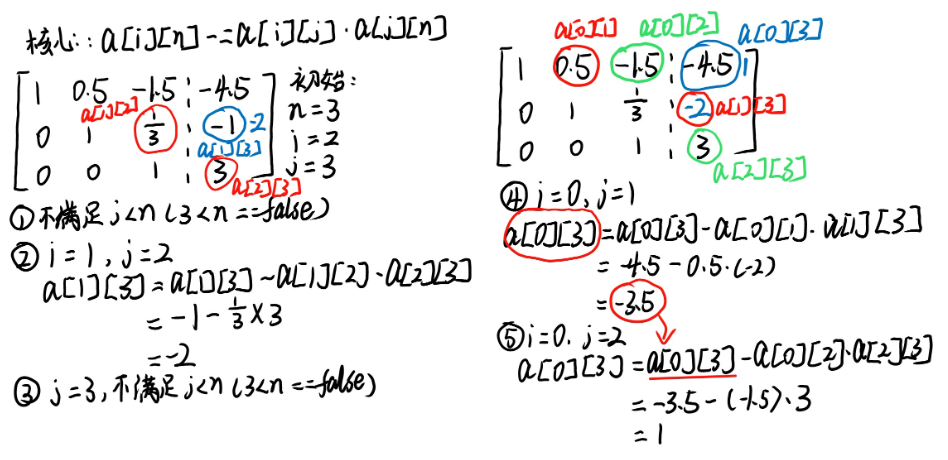
    for (int i = n - 1; i >= 0; i -- )
        for (int j = i + 1; j < n; j ++ )
            a[i][n] -= a[i][j] * a[j][n];		// 倒着将答案推出，即注1情况

    return 0; 									// 有唯一解
}


int main()
{
    scanf("%d", &n);
    for (int i = 0; i < n; i ++ )
        for (int j = 0; j < n + 1; j ++ )
            scanf("%lf", &a[i][j]);

    int t = gauss();
    if (t == 2) puts("No solution");
    else if (t == 1) puts("Infinite group solutions");
    else
    {
        for (int i = 0; i < n; i ++ )
        {
            if (fabs(a[i][n]) < eps) a[i][n] = 0;  // 去掉输出 -0.00 的情况
            printf("%.2lf\n", a[i][n]);
        }
    }

    return 0;
}

注：

四、组合数

$C_{a}^{b} = \frac{a*(a-1)…(a-b+1)}{123*…*b} = \frac{a!}{b!(a-b)!}$

4.1 递推法求组合数

例1：求组合数 I

给定n组询问，每组询问给定两个整数a,b，请你输出$C_{a}^{b}\mod (10^{9}+7)$的值，其中1≤n≤10000,1≤b≤a≤2000。

$C_{a}^{b} = C_{a-1}^{b} + C_{a-1}^{b-1}$

从a个苹果中选b个的方案数包含两大类：(红色苹果是其中一个苹果)

包含红色苹果$C_{a-1}^{b-1}$
不包含红色苹果$C_{a-1}^{b}$

// c[a][b] 表示从a个苹果中选b个的方案数
for (int i = 0; i < N; i ++ )
    for (int j = 0; j <= i; j ++ )
        if (!j) c[i][j] = 1;
        else c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod;

4.2 预处理逆元求组合数

例2：求组合数 II

给定n组询问，每组询问给定两个整数a,b，请你输出$C_{a}^{b}\mod (10^{9}+7)$的值，其中1≤n≤10000,1≤b≤a≤10^5。

首先预处理出所有阶乘取模的余数fact[N]，以及所有阶乘取模的逆元infact[N]。如果取模的数是质数，可以用费马小定理(快速幂)求逆元，即质数b的模p乘法逆元为$b^{p-2}$.

fact[i] = i! mod 10^9 + 7,infact[i] = (i!)^(-1) mod 10^9 + 7

计算组合数的结果为：$C_{a}^{b} =$fact[a]*infact[b-a]*infact[b].

注：引入逆元的目的：

按照组合数的定义进行计算时，$C_{a}^{b} = \frac{a!}{b!(a-b)!}$，除以一个数时，由于数值非常大，而$\frac{a}{b}\mod p \neq \frac{a \mod p}{b \mod p}$，故引入逆元infact[N]。

int qmi(int a, int k, int p)    // 快速幂模板
{
    int res = 1;
    while (k)
    {
        if (k & 1) res = (LL)res * a % p;
        a = (LL)a * a % p;
        k >>= 1;
    }
    return res;
}

// 预处理阶乘的余数和阶乘逆元的余数
fact[0] = infact[0] = 1;
for (int i = 1; i < N; i ++ )
{
    fact[i] = (LL)fact[i - 1] * i % mod;
    infact[i] = (LL)infact[i - 1] * qmi(i, mod - 2, mod) % mod;
}

4.3 Lucas定理求组合数

例：求组合数 III

1≤b≤a≤10^18,1≤p≤10^5

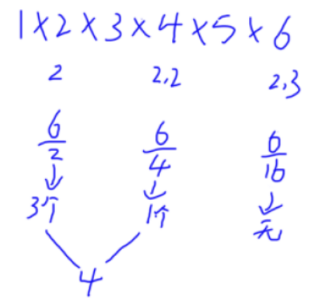
Lucas定理：若p是质数，则对于任意整数$1 \leq a \leq b$，有：$C_{a}^{b} = C_{a\mod p}^{b\mod p}*C_{a/p}^{b/p}(\mod p)$

证明：将a,b写为p进制形式：

$a = a_{k}*p^{k}+a_{k-1}*p^{k-1}+…+a_{0}*p^{0}$

$b = b_{k}*p^{k}+b_{k-1}*p^{k-1}+…+b_{0}*p^{0}$

又$(1+x)^{p} = C_{p}^{0}*1+C_{p}^{1}*x+C_{p}^{2}*x^{2}+…+C_{p}^{p}*p = 1+x^{p}(\mod p)$,

经过运算得证。

按照组合数的定义进行计算，$C_{a}^{b} = \frac{a!}{b!(a-b)!} = \frac{(a-b+1)*…*a}{b!}$，分子有b项。

int qmi(int a, int k, int p)  					// 快速幂模板
{
    int res = 1 % p;
    while (k)
    {
        if (k & 1) res = (LL)res * a % p;
        a = (LL)a * a % p;
        k >>= 1;
    }
    return res;
}

int C(int a, int b, int p)  					// 通过定理求组合数C(a, b)
{
    if (a < b) return 0;

    LL x = 1, y = 1;  							// x是分子，y是分母
    for (int i = a, j = 1; j <= b; i --, j ++ )
    {
        x = (LL) x * i % p;
        y = (LL) y * j % p;
    }

    return x * (LL)qmi(y, p - 2, p) % p;		// 除法使用快速幂求逆元
}

int lucas(LL a, LL b, int p)
{
    if (a < p && b < p) return C(a, b, p);
    return (LL)C(a % p, b % p, p) * lucas(a / p, b / p, p) % p;
}

4.4 分解质因数法求组合数

当我们需要求出组合数的真实值，而非对某个数的余数时，分解质因数的方式比较好用：

筛法求出范围内的所有质数
通过$C_{a}^{b} = \frac{a!}{b!(a-b)!}$这个公式求出每个质因子的次数。n!中p的次数是n / p + n / p^2 + n / p^3 + ...
用高精度乘法将所有质因子相乘

例：求组合数 IV

#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;

const int N = 5010;

int primes[N], cnt;     					// 存储所有质数
int sum[N];     							// 存储每个质数的次数
bool st[N];    								// 存储每个数是否已被筛掉

void get_primes(int n)     					// 线性筛法求素数
{
    for (int i = 2; i <= n; i ++ )
    {
        if (!st[i]) primes[cnt ++ ] = i;
        for (int j = 0; primes[j] <= n / i; j ++ )
        {
            st[primes[j] * i] = true;
            if (i % primes[j] == 0) break;
        }
    }
}

int get(int n, int p)						// 求n!中p出现的次数
{
    int res = 0;
    while (n)
    {
        res += n / p;
        n /= p;
    }
    return res;
}

vector<int> mul(vector<int> a, int b)		// 高精度乘低精度模板
{
    vector<int> c;
    int t = 0;
    for (int i = 0; i < a.size(); i ++ )
    {
        t += a[i] * b;
        c.push_back(t % 10);
        t /= 10;
    }
    while (t)
    {
        c.push_back(t % 10);
        t /= 10;
    }
    return c;
}

int main()
{
    int a, b;
    cin >> a >> b;

    get_primes(a);							// 预处理范围内的所有质数

    for (int i = 0; i < cnt; i ++ )			// 求每个质因数的次数,注1
    {
        int p = primes[i];					// p是当前的质数
        // 用分子里面 p 的个数减去分母里面 p 的个数。这里的计算组合数的公式为a!/(b!*(a-b)!),因此用 a 里面 p 的个数减去 b 里面 p 的个数和 (a-b) 里面 p 的个数
        sum[i] = get(a, p) - get(a - b, p) - get(b, p);
    }

    vector<int> res;
    res.push_back(1);

    for (int i = 0; i < cnt; i ++ )			// 用高精度乘法将所有质因子相乘
        // res*p^k,这里是k个p相乘,不是k*p,所以需要使用一个循环
        for (int j = 0; j < sum[i]; j ++ )
            res = mul(res, primes[i]);
	// 倒序打印res,由于采用小端存储,所以高位在后,从后往前打印即可
    for (int i = res.size() - 1; i >= 0; i -- ) printf("%d", res[i]);
    puts("");

    return 0;
}

注：对61行的注释：

问题问的是求$C_{a}^{b}$，转换为求$\frac{a!}{b!(a-b)!}$即可。我们的方法是，把a!转化为分解质因数的形式，即$a! = p_{1}^{c_{1}}p_{2}^{c_{2}}…*p_{k}^{c_{k}}$；a!中质数出现的次数$=\lfloor\frac{a}{p}\rfloor+\lfloor\frac{a}{p^{2}}\rfloor+\lfloor\frac{a}{p^{3}}\rfloor+…+\lfloor\frac{a}{p^{k}}\rfloor$。

4.5 卡特兰数

给定n个0和n个1，它们按照某种顺序排成长度为2n的序列，满足任意前缀中0的个数都不少于1的个数的序列的数量为：Cat(n) = C(2n, n) / (n + 1).

例：满足条件的01序列

给定n个 0和n个1，它们将按照某种顺序排成长度为2n的序列，求它们能排列成的所有序列中，能够满足任意前缀序列中0的个数都不少于1的个数的序列有多少个。

0代表向右走一格，1代表向上走一格：

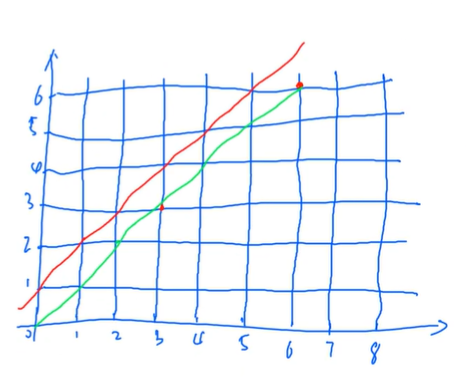
满足条件的01序列示意1

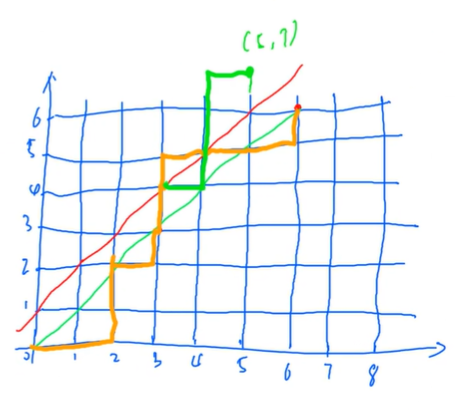
满足条件的01序列示意2

需满足$x \geq y$，则必须在红色下面(不得触碰红线)。则题述转化为：从(0,0)到(n,n)，不经过红色这条边的路径的个数。

当有触碰到红线的路径时，将从触碰到红线到末段的路线对红线作轴对称，终点必为(5,7)，故不合法的路径有$C_{12}^{5}$条。

则总合法路径的数量为$C_{12}^{6}-C_{12}^{5}$。

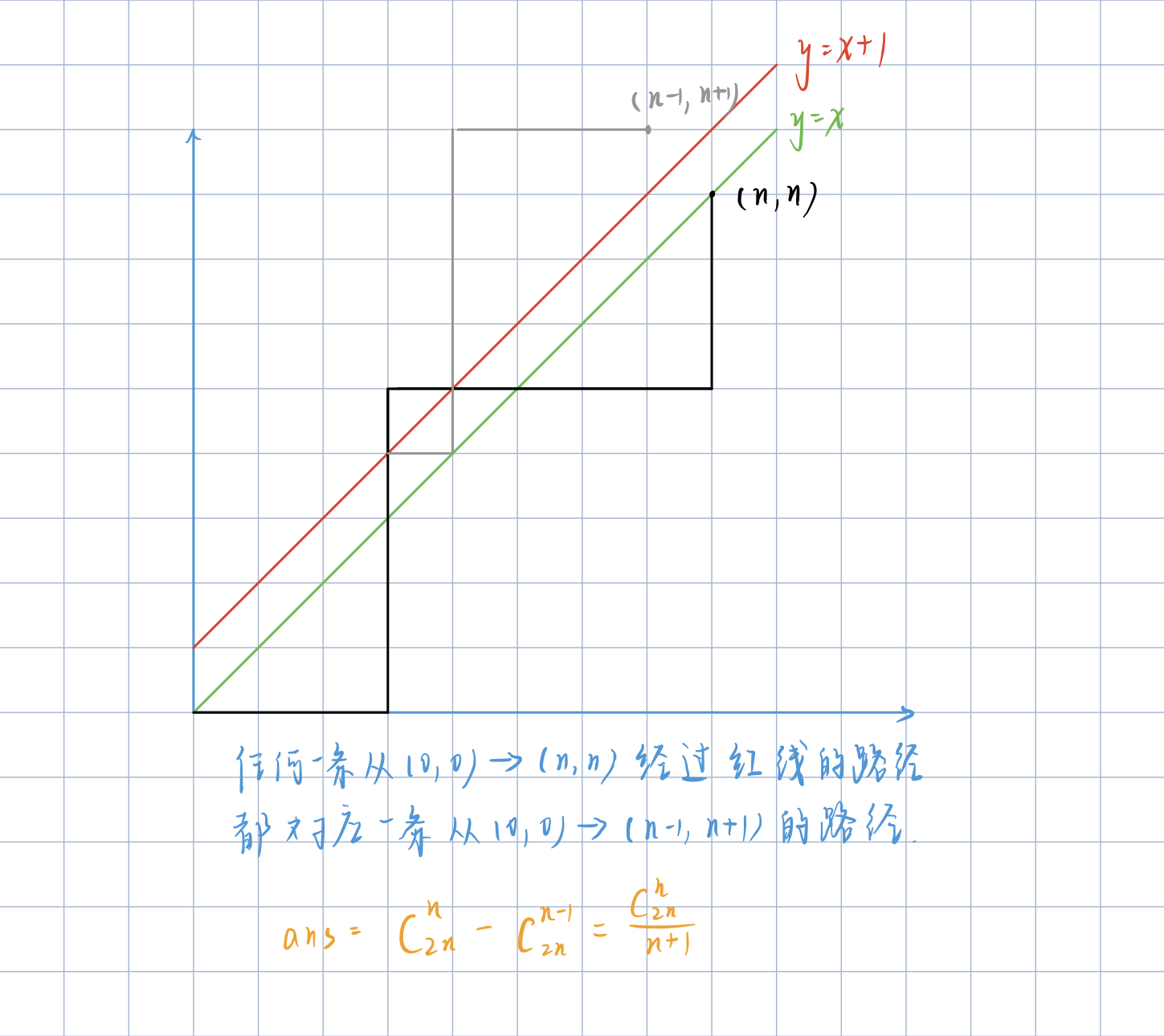
扩展到n的情况，总合法路径的数量为$C_{2n}^{n}-C_{2n}^{n-1} = \frac{C_{2n}^{n}}{n+1}$。示意图如下：

#include <iostream>
#include <algorithm>
using namespace std;

typedef long long LL;

const int N = 100010, mod = 1e9 + 7;


int qmi(int a, int k, int p)
{
    int res = 1;
    while (k)
    {
        if (k & 1) res = (LL)res * a % p;
        a = (LL)a * a % p;
        k >>= 1;
    }
    return res;
}


int main()
{
    int n;
    cin >> n;

    int a = n * 2, b = n;
    int res = 1;
    for (int i = a; i > a - b; i -- ) res = (LL)res * i % mod;

    for (int i = 1; i <= b; i ++ ) res = (LL)res * qmi(i, mod - 2, mod) % mod;

    res = (LL)res * qmi(n + 1, mod - 2, mod) % mod;

    cout << res << endl;

    return 0;
}

五、容斥原理

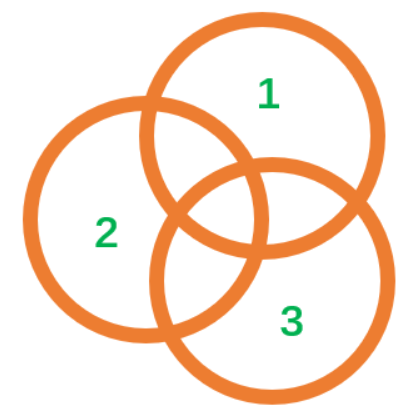
求$S=S_{1}\cup S_{2}\cup S_{3}$的面积：

$\begin{aligned}
S=& S_{1} \cup S_{2} \cup S_{3} \
=& S_{1}+S_{2}+S_{3} \
&-S_{1} \cap S_{2}-S_{1} \cap S_{3}-S_{2} \cap S_{3} \
&+S_{1} \cap S_{2} \cap S_{3}
\end{aligned}$

推广求$S=S_{1}\cup S_{2}\cup S_{3}\cup S_{4}$的面积：

$\begin{aligned}
S=& S_{1} \cup S_{2} \cup S_{3} \cup S_{4} \
=& S_{1}+S_{2}+S_{3}+S_{4} \
&-S_{1} \cap S_{2}-S_{1} \cap S_{3}-S_{1} \cap S_{4}-S_{2} \cap S_{3}-S_{2} \cap S_{4}-S_{3} \cap S_{4} \
&+S_{1} \cap S_{2} \cap S_{3}+S_{1} \cap S_{2} \cap S_{4}+S_{1} \cap S_{3} \cap S_{4}+S_{2} \cap S_{3} \cap S_{4} \
&-S_{1} \cap S_{2} \cap S_{3} \cap S_{4}
\end{aligned}$

若将面积作为集合看待，则容易推出：

设U中元素有n种不同的属性，而第i种属性称为$P_{i}$，拥有属性$P_{i}$的元素构成集合$S_{i}$，那么：

$\begin{aligned}
\left|\bigcup_{i=1}^{n} S_{i}\right|=& \sum_{i}\left|S_{i}\right|-\sum_{i<j}\left|S_{i} \cap S_{j}\right|+\sum_{i<j<k}\left|S_{i} \cap S_{j} \cap S_{k}\right|-\ldots \
&+(-1)^{m-1} \sum_{a_{i}<a_{i+1}}\left|\bigcap_{i=1}^{m} S_{a_{i}}\right|+\cdots+(-1)^{n-1}\left|S_{1} \cap \cdots \cap S_{n}\right|
\end{aligned}$

即：

$\left|\bigcup_{i=1}^{n} S_{i}\right|=\sum_{m=1}^{n}(-1)^{m-1} \sum_{a_{i}<a_{i+1}}\left|\bigcap_{i=1}^{m} S_{a_{i}}\right|$

由于$C_{n}^{0}+C_{n}^{1}+C_{n}^{2}+…+C_{n}^{n}=2^{n}$[注]，即$C_{n}^{1}+C_{n}^{2}+…+C_{n}^{n}=2^{n}-C_{n}^{0}=2^{n}-1$，故算法时间复杂度为$O(2^{n})$.

注：该式代表从n个数中选取任意多个数的方案数，每个元素包含选和不选两种情况，故总方案数为$2^{n}$.

例：能被整除的数

给定一个整数n和m个不同的质数$p_{1},p_{2},…,p_{m}$，请你求出1∼n中能被$p_{1},p_{2},…,p_{m}$中的至少一个数整除的整数有多少个。

本题可以根据容斥原理进行求解。设能被$P_{i}$整除的数的集合为$S_{i}$，则有$\left |S_{i} \right | = \frac{n}{P_{i}}$。

需要知道每个集合的大小$\left | S_{i} \right |$和集合与集合之间交集的大小。有公式：$\left |S_{i}\cap S_{j} \right | = \frac{n}{P_{i}*P_{j}}$。

推广有：$\left |S_{1}\cap S_{2}\cap … \cap S_{n} \right | = \frac{n}{P_{1}P_{2}…*P_{n}}$。

[代码实现思路]

每一个i代表一种可能的取法，最外层的循环遍历置2的m次方后，可以取完所有的取法；
- 有m个数，遍历2的m次方个数，即可通过二进制数表示哪个集合被筛选，如1010(m位)表示第2个和第4个质数被筛选
里面的循环就是提取出这个i值对应的取法；
再将提取出的取法代入公式。

#include <iostream>
#include <algorithm>
using namespace std;

typedef long long LL;

const int N = 20;

int p[N];

int main()
{
    int n, m;
    cin >> n >> m;

    // 用p数组存储m个质数
    for (int i = 0; i < m; i ++ ) cin >> p[i];

    int res = 0;
    // -----1、每一个i代表一种可能的取法，最外层的循环遍历至2的m次方后，可以取完所有的取法----
    // ① 为什么是2的m次方？最外层循环的作用是什么？
    // 从1开始枚举，枚举到1 << m（左移m位。左移一位相当于乘2，右移一位相当于除2），即2的m次方；
    for (int i = 1; i < 1 << m ; i ++ )
    {
        // t代表当前所有质数的乘积，s代表什么当前选法包含几个集合
        int t = 1, s = 0;
        // --------------------2、这个循环就是提取出这个i值对应的取法--------------------
        // 枚举m个质数(看选法是否包括它,包括它则进行相应计算)，依次计算容斥原理的公式
        for (int j = 0; j < m; j ++ ){
            // i右移j位与上1，即如果当前位是1的话
            // 这里用位运算,是为了求出哪一位上是1,从而计算出1对应的位置的集合的交集数
            if (i >> j & 1)
            {
                // (LL)t * p[j] > n
                // 如果t（已有的质数选法）乘上这个质数大于给定的数n，说明1∼n中的数不能被p整除
                // 此时直接返回break，跳过该方案(该方案是有误的)
                if ((LL)t * p[j] > n)
                {
                    t = -1;
                    break; // break的作用域是跳出整个循环
                }
                // 将该质数乘到t中
                t *= p[j];
                // s表示当前选法中有多少个集合,集合交的个数可以判断表达式符号的奇偶性
                s ++ ;
            }
        }
        // --------------------3、再将提取出的取法代入公式--------------------
        // 如果t不等于-1（-1是给定的flag值）
        if (t != -1)
        {
            // 根据容斥原理公式,这里其实是模拟（-1）^n-1,奇数个集合是加，偶数个集合是减
            if (s % 2) res += n / t;
            else res -= n / t;
        }
    }

    cout << res << endl;

    return 0;
}

注：

① 最外层循环的作用是什么？为什么是2的m次方？

for (int i = 1; i < 1 << m ; i ++ )

这个是用位运算来作枚举，从1枚举到2的m次方减1。

把i看做一个二进制数，如i = 5(十进制下)= 00101(二进制下)，表示p1、p3被选了；

最外层的循环的作用是枚举从1到2的m次方减1的数，然后求出每个数的能被p1,p2,…,pm中的数整除的个数。m位组成的二进制数可以代表集合的选取情况。

六、简单博弈论

6.1 NIM博弈

给定N堆物品，第i堆物品有$A_{i}$个。两名玩家轮流行动，每次可以任选一堆，取走任意多个物品，可把一堆取光，但不能不取。取走最后一件物品者获胜。两人都采取最优策略，问先手是否必胜。

我们把这种游戏称为NIM博弈。

把游戏过程中面临的状态称为局面。整局游戏第一个行动的称为先手，第二个行动的称为后手。若在某一局面下无论采取何种行动，都会输掉游戏，则称该局面必败。

所谓采取最优策略是指，若在某一局面下存在某种行动，使得行动后对面面临必败局面，则优先采取该行动。同时，这样的局面被称为必胜。我们讨论的博弈问题一般都只考虑理想情况，即两人均无失误，都采取最优策略行动时游戏的结果。

NIM博弈不存在平局，只有先手必胜和先手必败两种情况。

先手必胜状态：可以走到某一个必败状态
先手必败状态：走不到任何一个必败状态

定理：NIM博弈先手必胜，当且仅当A1 ^ A2 ^ ... ^ An != 0(^代表异或)

证明：

基于以上证明，有：

如果先手面对的局面是a1⊕a2⊕...⊕an≠0，那么先手总可以通过拿走某一堆若干个石子，将局面变成a1⊕a2⊕...⊕an=0。如此重复，最后一定是后手面临最终没有石子可拿的状态。先手必胜。
如果先手面对的局面是a1⊕a2⊕...⊕an=0，那么无论先手怎么拿，都会将局面变成a1⊕a2⊕...⊕an≠0，那么后手总可以通过拿走某一堆若干个石子，将局面变成a1⊕a2⊕...⊕an=0。如此重复，最后一定是先手面临最终没有石子可拿的状态。先手必败。

例：Nim游戏

#include <iostream>
#include <algorithm>
using namespace std;

const int N = 100010;

int main()
{
    int n;
    scanf("%d", &n);

    int res = 0;
    while (n -- )
    {
        int x;
        scanf("%d", &x);
        res ^= x;
    }

    if (res) puts("Yes");
    else puts("No");

    return 0;
}

6.2 SG函数

6.2.1 Mex运算

设S表示一个非负整数集合。定义mex(S)为求出不属于集合S的最小非负整数的运算，即：mex(S) = min{x}, x属于自然数，且x不属于S。

通俗的讲，即是：不存在S集合中的数中，最小的那个数。

6.2.2 SG函数

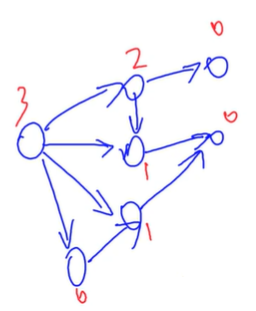
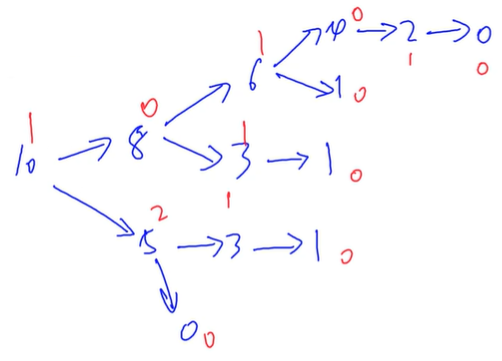
在有向图游戏中，对于每个节点x，设从x出发共有k条有向边，分别到达节点y1, y2,..., yk。

定义SG(x)为x的后继节点y1, y2, ..., yk的SG函数值构成的集合再执行mex(S)运算的结果，即：SG(x) = mex({SG(y1), SG(y2), …, SG(yk)})。易知SG(终点) = 0。

特别地，整个有向图游戏G的SG函数值被定义为有向图游戏起点s的SG函数值，即SG(G) = SG(s)。

SG函数图示

定理1：

有向图游戏的某个局面必胜，当且仅当该局面对应节点的SG函数值大于0；
有向图游戏的某个局面必败，当且仅当该局面对应节点的SG函数值等于0。

定理2：

设G1, G2,..., Gm是m个有向图游戏。定义有向图游戏G，它的行动规则是任选某个有向图游戏Gi，并在Gi上行动一步。

G被称为有向图游戏G1, G2,..., Gm的和。
有向图游戏的和的SG函数值等于它包含的各个子游戏SG函数值的异或和，即：SG(G) = SG(G1) ^ SG(G2) ^ ... ^ SG(Gm)。

证得：若先手面对的状态是xor!=0，则先手方总能使xor=0，即使后手面对的永远是必败态直到结束状态①，因此先手必胜；反之，必败。

例：集合-Nim游戏

#include <cstring>
#include <iostream>
#include <algorithm>
#include <unordered_set>
using namespace std;

const int N = 110, M = 10010;

int n, m;
int s[N], f[M];					//s存储的是可供选择的集合,f存储的是所有出现过的情况的sg值

int sg(int x)
{
    //记忆化搜索,因为取石子数目的集合是已经确定了的,所以每个数的sg值也都是确定的,如果存储过了,直接返回即可
    if (f[x] != -1) return f[x];

    unordered_set<int> S;		//因为在函数内部定义,所以下一次递归中的S不与本次相同
    for (int i = 0; i < m; i ++ )
    {
        int sum = s[i];			// sum表示当前遍历到的操作数量
        if (x >= sum) 	 		// 若x >= sum表明当前x可以取走sum个石子
            // 递归，将得到的sg值存入S,即先延伸到终点的sg值后,再从后往前排查出所有数的sg值
            S.insert(sg(x - sum));
    }

    for (int i = 0; ; i ++ )	// 从0开始遍历x可取的sg值，要保证为x未指向的最小的数
        if (!S.count(i)) 		// 表明当前x并未指向i这个值，即x可取i，且此时最小
            return f[x] = i;	// 将i存入f，并作为x的sg值返回
}

int main()
{
    cin >> m;
    for (int i = 0; i < m; i ++ ) cin >> s[i];
    cin >> n;

    memset(f, -1, sizeof f);	//初始化f数组

    int res = 0;
    for (int i = 0; i < n; i ++ )
    {
        int x;
        cin >> x;
        res ^= sg(x);			// 计算每堆石子sg值异或的结果
    }

    if (res) puts("Yes");
    else puts("No");

    return 0;
}

注：unordered_set_name.count(element)

此函数接受单个参数element，表示容器中是否存在需要检查的元素。

返回值：如果元素存在于容器中，则此函数返回1，否则返回0。

ShiQuLiZhi

https://www.qqzzss.top/2022/08/13/algorithmlearning/suan-fa-04-shu-xue-zhi-shi/

本博客所有文章除特别声明外，均采用 CC BY 4.0 许可协议。转载请注明来源 ShiQuLiZhi !

算法数据结构数学知识

计算机网络理论

2022-08-13 计算机学科理论

理论知识计算机网络

算法3:搜索与图论

2022-08-13 算法学习

算法数据结构

算法4:数学知识

一、质数与约数

1.1 质数的判定

1.2 分解质因数

1.3 筛素数

1.3.1 朴素筛法筛素数

1.3.2 线性筛法筛素数

1.4 约数

1.4.1 试除法求一个数的所有约数

1.4.2 约数个数

1.4.3 约数之和

1.4.4 最大公约数:欧几里得算法

二、数学定理

2.1 欧拉函数

2.1.1 求欧拉函数

2.1.2 筛法求欧拉函数

2.1.3 欧拉定理

2.2 快速幂

2.3 拓展欧几里得算法

2.4 中国剩余定理

三、高斯消元

四、组合数

4.1 递推法求组合数

4.2 预处理逆元求组合数

4.3 Lucas定理求组合数

4.4 分解质因数法求组合数

4.5 卡特兰数

五、容斥原理

六、简单博弈论

6.1 NIM博弈

6.2 SG函数

6.2.1 Mex运算

6.2.2 SG函数