算法课外思考题0907(动态变化的数据中获取最小值)

💡Author：信安2002钱泽枢(ShiQuLiZhi)

🚀欢迎访问我的作业合集：https://sxhthreo.github.io/categories/%E4%BD%9C%E4%B8%9A/

1.1 问题描述

给出策略在一系列可能动态变化（可增可减）的数据中获取最小值，并对你的策略或方案进行分析与评价。

1.2 算法思路

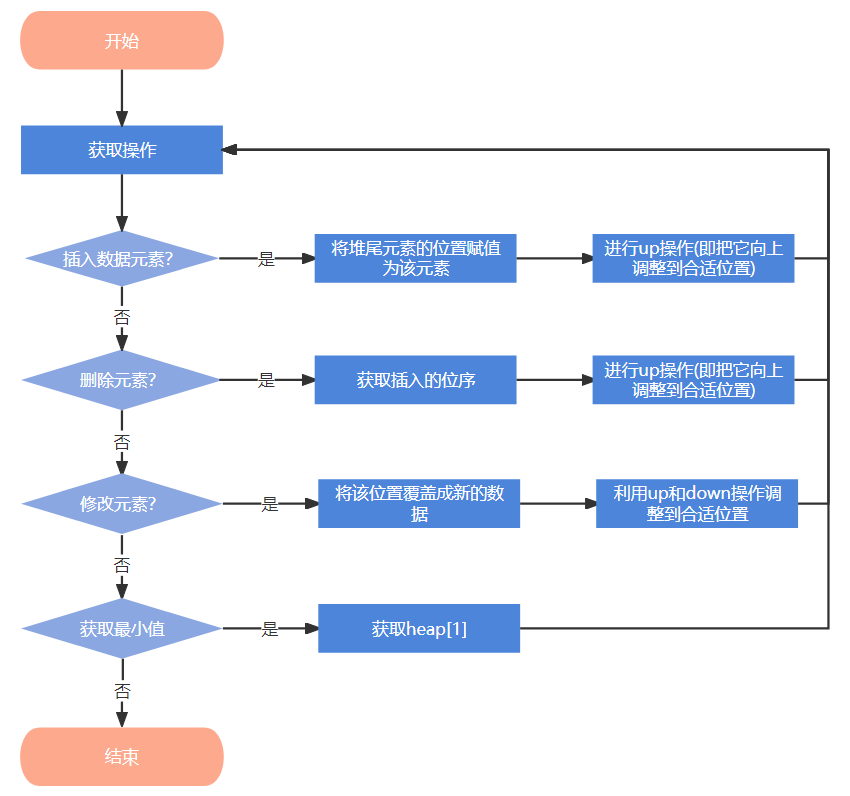
本题基于在可以动态变化的数据中获取最小值。在上学期《数据结构》课程中曾提到“堆”这种数据结构，堆的天然特性是可以通过访问首元素来获得最小值，故本算法基于堆来完成。每次插入一个数据元素时，将堆尾元素的位置赋值为该元素，并进行up操作(即把它向上调整到合适位置)；当删除数据元素时，可以通过获取它插入的位序，并将该位置覆盖成堆尾元素，再利用up和down操作调整到合适位置；当修改数据元素时，将该位置覆盖成新的数据，再利用up和down操作调整到合适位置；则当要获取最小值时只要获取heap[1]即可。算法复杂度分析详见1.6节。

1.3 算法图解

1.4 代码设计

程序设计由类Heap与main函数两大部分组成。类的功能设计描述如下：

class Heap 
{
public:
	void heap_swap(int a, int b)
	{
		swap(ph[hp[a]], ph[hp[b]]);		//将映射关系交换
		swap(hp[a], hp[b]);
		swap(heap[a], heap[b]);
	}

	void down(int u)
	{
		int t = u;
		if (u * 2 <= count && heap[u * 2] < heap[t]) t = u * 2;
		if (u * 2 + 1 <= count && heap[u * 2 + 1] < heap[t]) t = u * 2 + 1;
		if (u != t)			//当前根节点不是最小值
		{
			heap_swap(u, t);	//将两个节点交换
			down(t);			//进行可能的向下换操作
		}
	}

	void up(int u)
	{
		while (u / 2 && heap[u] < heap[u / 2])
		{
			heap_swap(u, u / 2);
			u = u / 2;
		}
	}

	void AddElement(int element)
	{
		heap[++count] = element;
		ph[++addrecord] = count, hp[count] = addrecord;		//添加插入次序与堆中节点的映射关系
		up(count);
	}

	void DelElement(int operate)
	{
		int k = ph[operate];
		heap_swap(k, count);		//将堆尾和插入位置交换
		count--;
		down(k);					//down和up两个操作会执行其中一个
		up(k);
	}

	void AlterElement(int operate,int element)
	{
		int k = ph[operate];
		heap[k] = element;
		down(k);					//down和up两个操作会执行其中一个
		up(k);
	}

	int GetAddRecord()
	{
		return addrecord;
	}

	int GetMin()
	{
		return heap[1];
	}

	void Init()
	{
		count = 0;
		addrecord = 0;
	}

private:
	int heap[N], ph[N], hp[N];		//h数组存储堆,ph数组存储第j个插入的数的下标,hp数组存储堆内下标为k的点的插入顺序
	int count;				//count记录堆中的元素数量
	int addrecord;			//addrecord记录插入的记录
};

主函数在附录中给出。

1.5 测试结果

程序主要包含插入元素、删除元素、修改元素、获取最小值四个功能。通过不断插入、删除、修改元素、获取最小值，覆盖了所有可能情况，运行的结果都是正确的、符合预期的。可以看出，代码具有正确性、鲁棒性。具体的包含main函数的代码详见附录。

1.6 总结与讨论

本算法考虑了数据可能进行的增加、删除与修改操作，并利用堆这一数据结构的天然优势，完成了在动态变化的数据中获取最小值的问题。本算法最大的时间消耗是堆的排序。

假设节点数为n，堆排序过程中最多需要进行n - 1次调换，也就是需要n-1次堆调整，每次堆调整的时间复杂度为O(logn) ，那么总时间复杂度就是(n - 1)O(logn) = O(nlogn)。

建堆并进行堆排序后，获取最小值只要访问heap[1]即可，仅需在O(1)时间内进行完成，故本算法的时间效率是比较高的。算法空间消耗仅来源于堆的存放与ph[N], hp[N]数组的空间消耗(ph数组存储第j个插入的数的下标,hp数组存储堆内下标为k的点的插入顺序)及相关变量的存储，空间消耗也较低。本算法可以满足本问题的需求。

附：源代码

//给出策略在一系列可能动态变化（可增可减）的数据中获取最小值
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;

const int N = 10;

class Heap 
{
public:
	void heap_swap(int a, int b)
	{
		swap(ph[hp[a]], ph[hp[b]]);		//将映射关系交换
		swap(hp[a], hp[b]);
		swap(heap[a], heap[b]);
	}

	void down(int u)
	{
		int t = u;
		if (u * 2 <= count && heap[u * 2] < heap[t]) t = u * 2;
		if (u * 2 + 1 <= count && heap[u * 2 + 1] < heap[t]) t = u * 2 + 1;
		if (u != t)				//当前根节点不是最小值
		{
			heap_swap(u, t);	//将两个节点交换
			down(t);			//进行可能的向下换操作
		}
	}

	void up(int u)
	{
		while (u / 2 && heap[u] < heap[u / 2])
		{
			heap_swap(u, u / 2);
			u = u / 2;
		}
	}

	void AddElement(int element)
	{
		heap[++count] = element;
		ph[++addrecord] = count, hp[count] = addrecord;
		up(count);
	}

	void DelElement(int operate)
	{
		int k = ph[operate];
		heap_swap(k, count);		//将堆尾和插入位置交换
		count--;
		down(k);					//down和up两个操作会执行其中一个
		up(k);
	}

	void AlterElement(int operate,int element)
	{
		int k = ph[operate];
		heap[k] = element;
		down(k);				//down和up两个操作会执行其中一个
		up(k);
	}

	int GetAddRecord()
	{
		return addrecord;
	}

	int GetMin()
	{
		return heap[1];
	}

	void Init()
	{
		count = 0;
		addrecord = 0;
	}

private:
	int heap[N], ph[N], hp[N];		//h数组存储堆,ph数组存储第j个插入的数的下标,hp数组存储堆内下标为k的点的插入顺序
	int count;				//count记录堆中的元素数量
	int addrecord;			//addrecord记录插入的记录
};

void PrintBoard()
{
	cout << "-------请输入您要进行的操作-------" <<endl;
	cout << "A.插入元素" << endl;
	cout << "B.删除元素" << endl;
	cout << "C.修改元素" << endl;
	cout << "D.获取最小值" << endl;
	cout << "E.退出系统" << endl;
}

int main()
{
	Heap heap;
	heap.Init();
	PrintBoard();
	while (true)
	{
		char input;
		int element, operate;
		cin >> input;
		switch (input)
		{
		case 'A': 
			cout << "请输入您要插入的数:" << endl;
			cin >> element;
			heap.AddElement(element);
			cout << "操作成功!当前是您的第" << heap.GetAddRecord() << "次增加元素操作~";
			break;
		case 'B':
			cout << "请输入您要删除的元素的操作次数编号:" << endl;
			cin >> operate;
			heap.DelElement(operate);
			cout << "操作成功!";
			break;
		case 'C':
			cout << "请输入您要修改的元素的操作次数编号及要修改为的元素" << endl;
			cin >> operate >> element;
			heap.AlterElement(operate,element);
			cout << "操作成功!";
			break;
		case 'D':
			cout << "当前序列的最小值为:" << heap.GetMin() << "!";
		}
		if (input == 'E') break;
		cout << "请输入您要继续的操作~" << endl;
	}
	return 0;
}