💡Author:信安2002钱泽枢(ShiQuLiZhi)
🚀欢迎访问我的作业合集:https://sxhthreo.github.io/categories/%E4%BD%9C%E4%B8%9A/
1.1 问题描述
给出不同策略求两个非负整数的最大公约数,并进行性能分析。
1.2 算法思路
给出以下四种算法求两个非负整数的最大公约数:
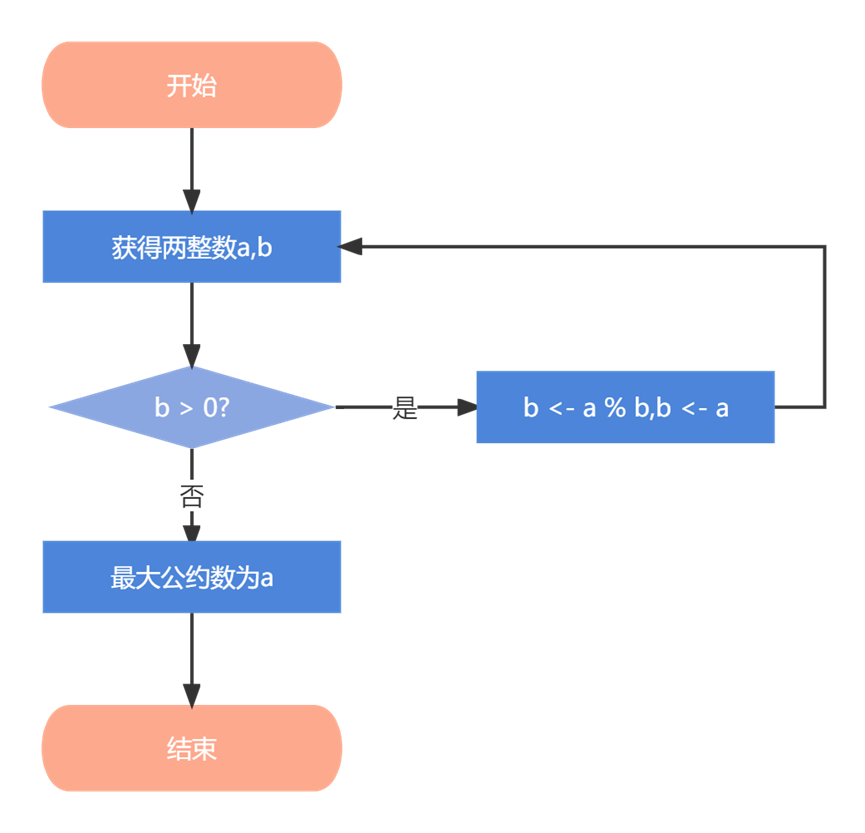
辗转相除法:有计算公式:
gcd(a,b) = gcd(b,a mod b)。若b > 0,则将a % b的值赋值为b,将b的值赋值为a,重复以上过程,直至b = 0,则最大公约数为a。穷举法:首先得到
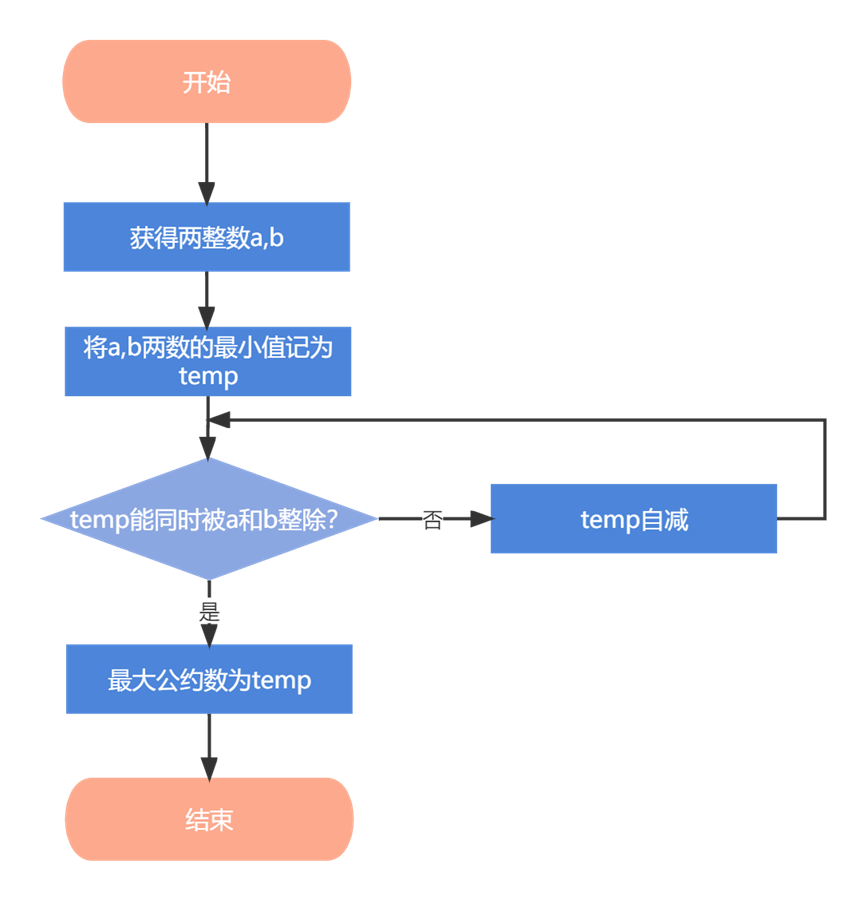
a,b两数的最小值(记为temp),然后进入循环,找到一个数能同时被a和b整除;每次判断,若满足条件则结束循环,否则temp自减,重复以上过程,则最大公约数为temp。更相减损法:
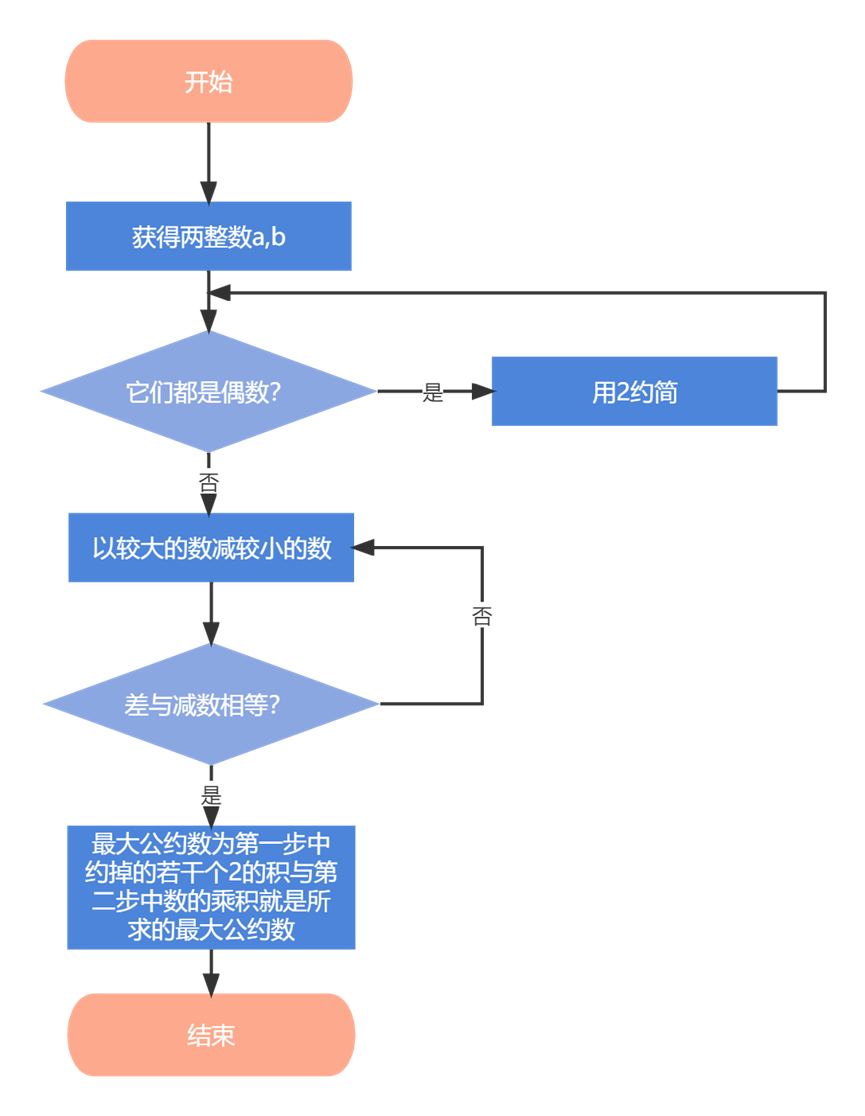
第一步:任意给定两个正整数,判断它们是否都是偶数:若是,则用2约简;若不是则执行第二步。
第二步:以较大的数减较小的数,接着把所得的差与较小的数比较,继续操作,直到所得的减数和差相等为止。
则第一步中约掉的若干个2的积与第二步中数的乘积就是所求的最大公约数。
Stein算法:主要用于解决超大数取模给欧几里得算法带来局限的问题。
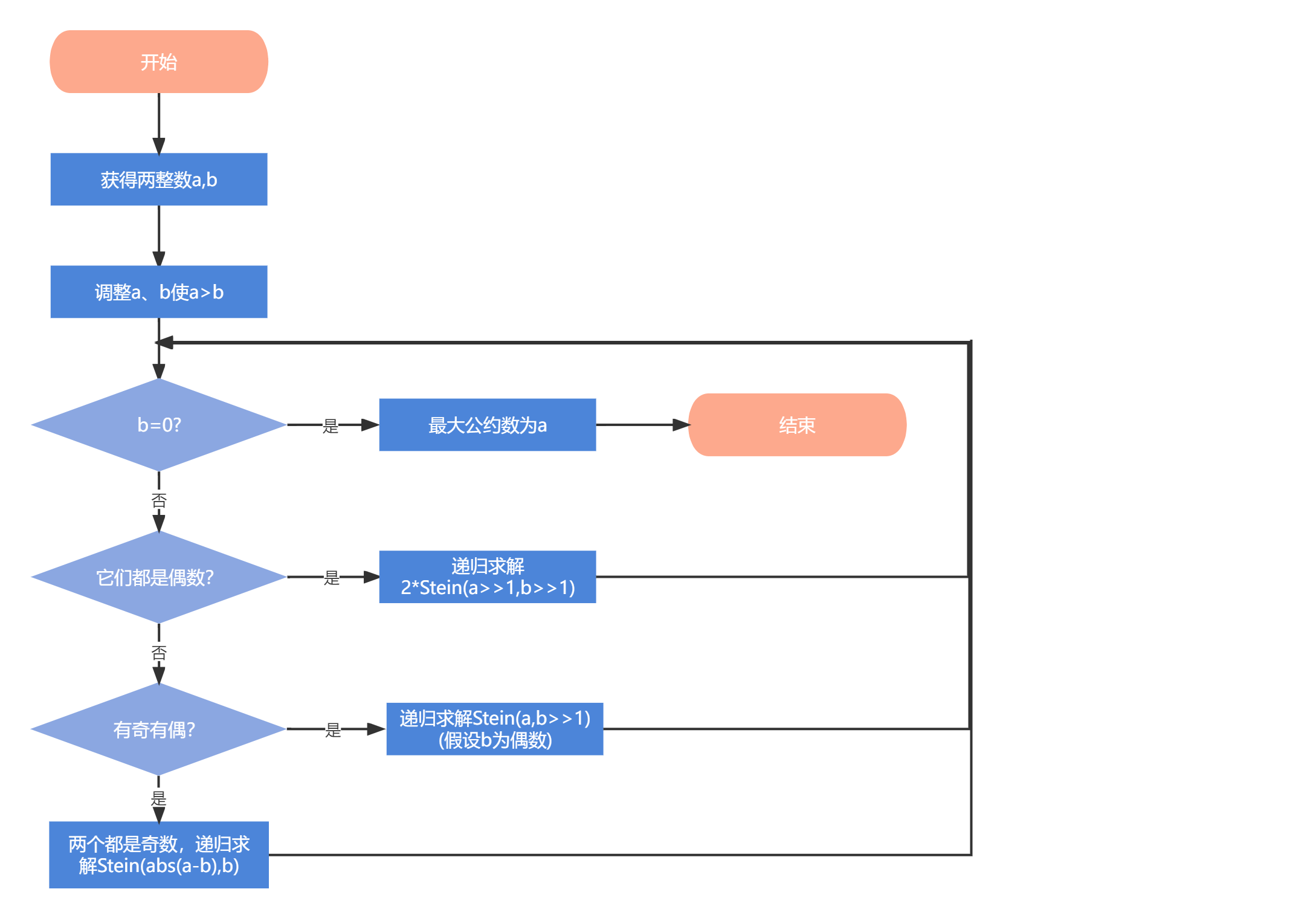
Stein递归算法(Stein(A,B))的步骤如下:
1)调整A、B使A>B
2)若A、B都是偶数,则记录下公因子2,然后递归求解2*Stein(A>>1,B>>1)
3)若A为奇数、B为偶数,则递归求解Stein(A,B>>1)
若B为奇数、A为偶数,则递归求解Stein(A>>1,B)
4)若两个都为奇数,则递归求解Stein(abs(A-B),B)
当B等于0时,得到最大公约数为A。
证明:设在某一次过程中
A、B的最大公因子为D,可得A=k*D,B=h*D;(A>B -> k>h), 所以A-B=|k-h|*D。A、B都为奇数,有奇偶数乘积奇偶性可得,D,k,h都为奇数。所以|k-h|一定是偶数,与h互质,所以A-B与B的最大公因数依旧为D。故Stein(A,B) = Stein(abs(A-B),B)。
1.3 算法图解
- 辗转相除法:
- 穷举法:
- 更相减损法:
- Stein算法:
1.4 代码设计
- 辗转相除法:
int gcd(int a, int b)
{
return b ? gcd(b, a % b) : a;
}- 穷举法:
int gcd2(int a, int b)
{
int temp;
temp = (a > b) ? b : a; //取a,b两数的最小值
while (temp > 0)
{
if (a % temp == 0 && b % temp == 0) //找到一个数能同时被a和b整除,则终止循环
{
break;
}
temp--;
}
return temp;
}- 更相减损法:
int gcd3(int a, int b)
{
//都为偶数的情况
int n = 1;
while ((a % 2 == 0) && (b % 2 == 0)) //直到有一方不是偶数 跳出循环
{
n *= 2;
a = a / 2;
b = b / 2;
}
while (1)
{
if (a < b) //交换,保证 a > b
{
int temp = a;
a = b;
b = temp;
}
int sub = a - b;
if (b == sub) //判断差和被减数是否相等,相等则跳出
break;
else {
a = b;
b = sub;
}
}
return b * n;
}- Stein算法:
int stein(int a, int b) {
if (a < b) swap(a, b);
if (b == 0) return a;
if ((a & 1) == 0 && (b & 1) == 0)
return stein(a >> 1, b >> 1) << 1;
else if (a & 1 && (b & 1) == 0)
return stein(a, b >> 1);
else if (b & 1 && (a & 1) == 0)
return stein(a >> 1, b);
else
return stein(a - b, b);
}1.5 测试结果
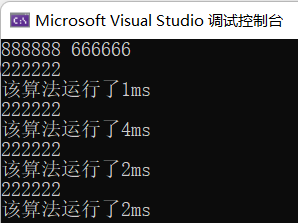
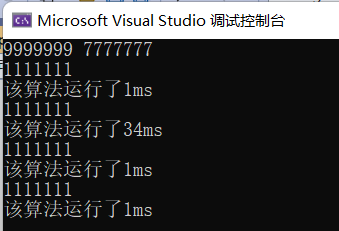
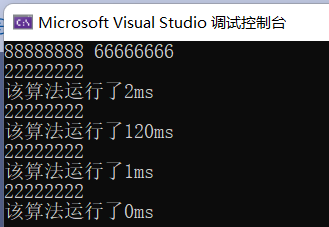
可以看到,辗转相除法、更相减损法、Stein算法都有较好的时间性能,而穷举法对于求解较大的两个数最大公约数的运行时间较长。
1.6 总结与讨论
我们来看四种算法的时间复杂度:
首先是辗转相除法。

于是得到 $a=u_0≥F_n,b=u_1≥F_{n−1}$。
也就是说如果欧几里得算法需要做n次模运算,则b必定不小于 $F_{n−1}$。
根据斐波那契数列的性质, 有$F_{n-1}>\frac{(1.618)^{n}}{\sqrt{5}}$,即$b>\frac{(1.618)^{n}}{\sqrt{5}}$,所以模运算的次数为$O(logb)$,则该算法的时间复杂度为$O(logb)$。
接下来是穷举法。穷举法是从a、b两数的最小值开始,最坏将减至1,穷举法是时间复杂度是O(min(a,b))的。
更相减损法则避免了取模运算,但算法性能不稳定,最坏时间复杂度为O(max(a, b)));
Stein算法不但避免了取模运算,而且算法性能稳定,采取时间性能高效的移位运算,时间复杂度为O(log(max(a, b)))。在大数据情况下,Stein算法具有较好的时间性能,被广泛应用。
2.1 问题描述
结合折半查找思路,给出三分查找的实现方法,并性能分析。
2.2 算法思路
三分查找的原理和二分查找的原理基本相同,都是在一个有序序列中查找元素,有所不同的是每次比较的不是中位元素,而是1/3处的元素和2/3处的元素。通过两次比较,我们可以将查找的范围缩减为原来的1/3,使查找效率提高。
2.3 算法图解
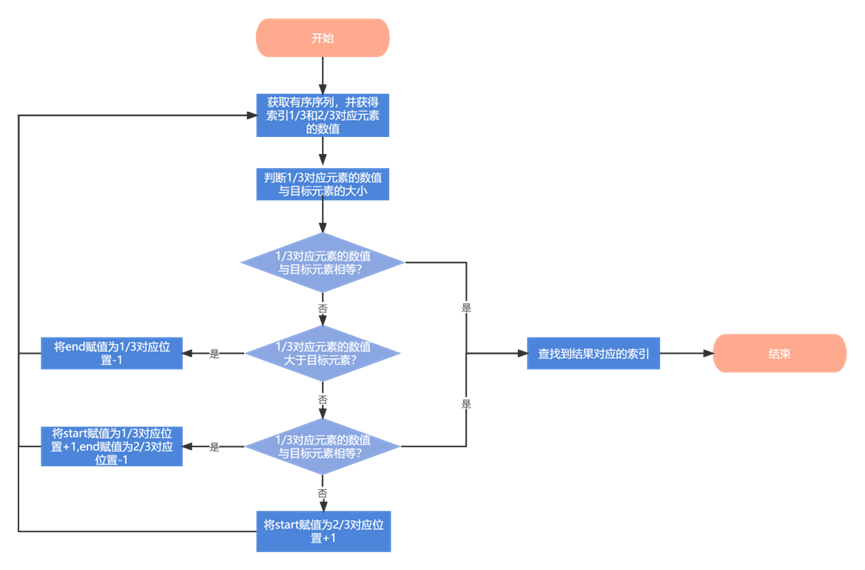
2.4 代码设计
//判断大小
int Condition(int a, int b)
{
if (a == b) return 0;
else
return a > b ? 1 : -1;
}
//三分查找
int TripleSearch(int a[], int start, int end, int target) {
if (start > end)
return -1;
int One_Third = start + (end - start) / 3;
int Two_Third = end - (end - start) / 3;
int Cond_1 = Condition(a[One_Third], target);
switch (Cond_1)
{
case 0:return One_Third;
case 1:return TripleSearch(a, start, One_Third - 1, target);
}
int Cond_2 = Condition(a[Two_Third], target);
switch (Cond_2)
{
case 0:return Two_Third;
case 1:return TripleSearch(a, One_Third + 1, Two_Third - 1, target);
case -1:return TripleSearch(a, Two_Third + 1, end, target);
}
}2.5 测试结果
多次测试,测试结果均正确且符合题意。
2.6 总结与讨论
三分查找通过比较与1/3、2/3位置元素之间的关系,将查找的范围缩减为原来的1/3,时间复杂度降为O(log_3n),在数据量较大的情况下,算法效率相比二分查找有比较明显的提高。
三分查找还可以用于搜索二次函数的最小值。在这个问题中,如果使用二分查找,我们在取完mid之后, 并不知道答案可能出现在左右哪个区间;而使用三分查找时,我们会将区间分成三份,将两个端点分别叫做m1和m2。我们要求的是函数的最小值,需要进行极值逼近。我们直接根据函数图像来分析,根据下图我们可以看到,m1和m2的值和它们距离极值点的远近是有关系的。离极值点越近,函数值越小(也有可能越大,视函数而定)。
在下图中,f(m2) < f(m1),则m2离极值点的距离更近。我们要缩小区间范围,逼近极值点,所以我们取start = m1。
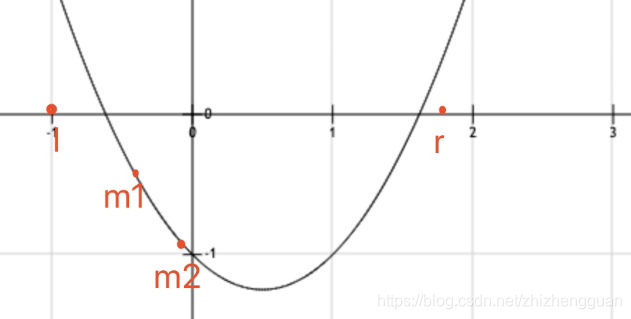
在这里,我们每次通过比较两个值的大小,缩小三分之一的区间,直到最后区间的范围小于我们设置的阈值为止,从而得到二次函数的最小值。
附:源代码
算法题1:
#include<iostream>
#include<ctime>
using namespace std;
int gcd(int a, int b) //辗转相除法
{
return b ? gcd(b, a % b) : a;
}
int gcd2(int a, int b) //穷举法
{
int temp;
temp = (a > b) ? b : a;
while (temp > 0)
{
if (a % temp == 0 && b % temp == 0) //找到一个数能同时被a和b整除,则终止循环
{
break;
}
temp--;
}
return temp;
}
int gcd3(int a, int b)
{
//都为偶数的情况
int n = 1;
while ((a % 2 == 0) && (b % 2 == 0))//直到有一方不是偶数 跳出循环
{
n *= 2;
a = a / 2;
b = b / 2;
}
while (1)
{
if (a < b) //交换,保证 a > b
{
int temp = a;
a = b;
b = temp;
}
int sub = a - b;
if (b == sub) //判断差和被减数是否相等,相等则跳出
break;
else {
a = b;
b = sub;
}
}
return b * n;
}
int stein(int a, int b) {
if (a < b) swap(a, b);
if (b == 0) return a;
if ((a & 1) == 0 && (b & 1) == 0)
return stein(a >> 1, b >> 1) << 1;
else if (a & 1 && (b & 1) == 0)
return stein(a, b >> 1);
else if (b & 1 && (a & 1) == 0)
return stein(a >> 1, b);
else
return stein(a - b, b);
}
int main()
{
time_t begin, end;
int a, b;
cin >> a >> b;
begin = clock();
cout << gcd(a, b) << endl;
end = clock();
cout << "该算法运行了" << double(end - begin) << "ms" << endl;
begin = clock();
cout << gcd2(a, b) << endl;
end = clock();
cout << "该算法运行了" << double(end - begin) << "ms" << endl;
begin = clock();
cout << gcd3(a, b) << endl;
end = clock();
cout << "该算法运行了" << double(end - begin) << "ms" << endl;
begin = clock();
cout << stein(a, b) << endl;
end = clock();
cout << "该算法运行了" << double(end - begin) << "ms" << endl;
return 0;
}算法题2:
#define _CRT_SECURE_NO_WARNINGS 1
#include<iostream>
#define N 10
using namespace std;
//判断大小
int Condition(int a, int b)
{
if (a == b) return 0;
else
return a > b ? 1 : -1;
}
//三分查找
int TripleSearch(int a[], int start, int end, int target) {
if (start > end)
return -1;
int One_Third = start + (end - start) / 3;
int Two_Third = end - (end - start) / 3;
int Cond_1 = Condition(a[One_Third], target);
switch (Cond_1)
{
case 0:return One_Third;
case 1:return TripleSearch(a, start, One_Third - 1, target);
}
int Cond_2 = Condition(a[Two_Third], target);
switch (Cond_2)
{
case 0:return Two_Third;
case 1:return TripleSearch(a, One_Third + 1, Two_Third - 1, target);
case -1:return TripleSearch(a, Two_Third + 1, end, target);
}
}
int main() {
int a[N] = { 0,1,4,6,7,8,9,25,55,88 };
int length = sizeof(a) / sizeof(a[0]); //数组长度
int target;
cout << "请输入想查找的元素:" << endl;
cin >> target;
int result = TripleSearch(a, 0, length - 1, target);
if (result == -1)
cout << "没有此元素" << endl;
else
cout << "该元素的索引为" << result << endl;
return 0;
}
